Problemas aritméticos verbales en los libros castellano-leoneses y andaluces
Arithmetic word problems in Castilian-Leonesian and Andalusian textbooks
https://doi.org/10.4438/1988-592X-RE-2024-406-641
Santiago Vicente Martín
https://orcid.org/0000-0002-2072-8133
Universidad de Salamanca
Marta Ramos Baz
https://orcid.org/0000-0002-9643-6495
Universidad de Salamanca
Mª. Mercedes Rodríguez Sánchez
https://orcid.org/0000-0002-1020-6681
Universidad de Salamanca
Beatriz Sánchez-Barbero
https://orcid.org/0000-0001-9118-2118
Universidad de Salamanca
Rosario Sánchez Fernández
https://orcid.org/0000-0002-7984-1894
Universidad de Salamanca
Resumen
Los resultados de evaluaciones del rendimiento en matemáticas como TIMSS, en las que la resolución de problemas es la piedra angular, muestran que el rendimiento los alumnos de Castilla y León es significativamente superior al de los alumnos de Andalucía. Estas diferencias parecen deberse a algunos aspectos señalados por el propio TIMSS (como el Índice Social y Económico), aunque también podrían deberse en algún grado a determinados elementos del proceso de enseñanza-aprendizaje, como el libro de texto, puesto que se usan de manera intensiva en las aulas. De hecho, los libros utilizados en países con alumnos más competentes en matemáticas incluyen más problemas, y problemas más variados y difíciles que los libros de otros países. El objetivo del presente trabajo es determinar si los libros de matemáticas de Primaria que se utilizan en Castilla y León son diferentes a los que se utilizan en Andalucía, en relación con el aprendizaje de la resolución de problemas aritméticos verbales. Para ello, en un primer estudio, se determina qué libros se utilizan con más frecuencia en cada comunidad autónoma, y en un segundo estudio, se analizan libros de 3º de Primaria de los proyectos editoriales más utilizados en cada comunidad autónoma en relación con la cantidad de tareas destinadas a resolver problemas, y la variedad y nivel de dificultad semántico-matemática de esos problemas. Los resultados indicaron que, aunque los libros más frecuentes en ambas comunidades pertenecen a proyectos editoriales diferentes, los libros más utilizados en Castilla y León y Andalucía eran similares respecto a las variables analizadas, encontrándose como única diferencia una mayor cantidad de problemas en los libros castellano-leoneses. Estos resultados contrastan con los obtenidos en comparaciones internacionales de libros de texto, y apuntan a una mayor influencia de otras variables en las diferencias de rendimiento de los alumnos de ambas comunidades.
Palabras clave: Libro de texto, enseñanza primaria, resolución de problemas, aritmética, análisis comparativo, análisis de contenido.
Abstract
The results of mathematics achievement assessments such as TIMSS, in which problem solving is the cornerstone, show that the performance of students in Castile and Leon is significantly higher than that of students in Andalusia. These differences seem to be due to some aspects pointed out by TIMSS (such as the Social and Economic index), although they could also be due to some degree to certain elements of the teaching-learning process, such as the textbook, since they are used intensively in the classroom. In fact, the books used in countries with more proficient students in mathematics include more problems, and more varied and difficult problems than books from other countries. The aim of the present work is to determine whether the primary mathematics textbooks used in Castile and Leon are different from those used in Andalusia, in relation to the learning of verbal arithmetic problem solving. For this purpose, in a first study, we determined which books are most frequently used in each autonomous community, and in a second study we analyzed 3rd grade primary school books from the most widely used textbooks in each autonomous community in relation to the number of tasks aimed at solving problems, and the variety and level of semantic-mathematical difficulty of these problems. The results indicated that, although the most frequently used books in both communities belong to different publishing projects, the most used books in Castile and Leon and Andalusia were very similar with respect to the variables analyzed, the only difference being a greater number of problems in the Castilian-Leonese books. These results contrast with those obtained in international comparisons of textbooks and point to a greater influence of other variables in the differences in student performance in both autonomous communities.
Keywords: textbook, primary education, problem solving, arithmetic, comparative analysis, content analysis.
Introducción
La resolución de problemas es la piedra angular del currículo de matemáticas de la mayoría de los sistemas educativos del mundo (Philpot et al., 2021) y de los marcos teóricos de las evaluaciones internacionales de rendimiento en matemáticas (Mullis et al., 2020). En este sentido, el marco teórico del Trends in International Mathematics and Science Study (TIMSS) define la resolución de problemas como la habilidad de resolver una variedad amplia de situaciones, aplicando los conocimientos matemáticos necesarios para realizar razonamientos de diferentes tipos y niveles de dificultad (Lindquist et al., 2017).
Los resultados de las evaluaciones internacionales muestran que no todos los países ni sus diferentes regiones están siendo igual de eficaces al desarrollar en sus alumnos la habilidad de resolver problemas. Para comprender el origen de esas diferencias, TIMSS proporciona datos sobre algunas variables educativas y socio-culturales: entorno familiar, composición y recursos de la escuela, clima escolar o la seguridad y disciplina del centro escolar (Mullis et al., 2020). Además de esas variables, otros elementos más concretos de la práctica educativa, como los libros de texto, influyen en el aprendizaje de los alumnos (Fagginger et al., 2016; Sievert et al., 2019, 2021).
Considerando lo anterior, en el presente trabajo se pretende comprobar si en dos comunidades autónomas españolas, cuyos alumnos han mostrado niveles de competencia matemática muy dispares, se utilizan libros diferentes, tanto en relación con su presencia en las aulas, como con la cantidad y variedad de problemas aritméticos verbales (en adelante, PAV) que contienen.
Diferencias en el Rendimiento en Resolución de Problemas
Uno de los objetivos de los programas como TIMSS es evaluar el éxito que alcanzan diferentes sistemas educativos al desarrollar distintas habilidades matemáticas en los alumnos, entre las que destaca la resolución de problemas (Lindquist et al., 2017). TIMSS establece diferentes niveles de rendimiento en función de las puntuaciones de los alumnos, que implican distintos grados de habilidad para resolver problemas. Los alumnos con un nivel bajo tendrían dificultades para resolver cualquier problema; los alumnos con un nivel intermedio únicamente podrían resolver problemas rutinarios; los alumnos con nivel alto resolverían problemas de dos pasos que requieran la comprensión conceptual de los números enteros; finalmente, los alumnos con un nivel avanzado podrían resolver problemas complejos de múltiples pasos que requieran comprensión y razonamiento (Mullis et al., 2020).
Los resultados de TIMSS (2016) en España revelaron que, en Castilla y León (en adelante, CyL), el porcentaje de alumnos de 4º de Primaria con niveles alto (33%) y avanzado (7%) es significativamente mayor que en Andalucía (18% y 2%, respectivamente). Asimismo, se encontraron diferencias significativas en todos los dominios evaluados, tanto de contenido (números, formas y medidas geométricas y representaciones de datos), como cognitivos (conocer, razonar y aplicar).
Las diferencias de rendimiento entre alumnos de distintos países y regiones parecen deberse a múltiples causas: implicación de las familias en la educación escolar, importancia de la educación para la sociedad, presupuesto dedicado a la educación, o formación del profesorado (Rao et al., 2010). Los datos del propio TIMSS y de otros informes, como PISA, indican una fuerte correlación entre el rendimiento en matemáticas y el Índice Social, Económico y Cultural de las familias (ISEC, ver Instituto Nacional de Evaluación Educativa, I.N.E.E., 2023). Otros estudios atribuyeron las diferencias entre regiones de un mismo país a otros factores (creencias epistemológicas de los profesores, expectativas laborales de los alumnos tras su escolaridad, o determinadas variables instruccionales, como el tiempo y tipo de instrucción que reciben los alumnos, ver Hippe et al., 2018). En España, las diferencias entre alumnos castellano-leoneses y andaluces se han atribuido a factores generales y difíciles de modificar, como un mayor ISEC de las familias, una mayor equidad del sistema educativo de CyL o a una mayor ansiedad ante las matemáticas de los alumnos andaluces (I.N.E.E., 2023). No obstante, el análisis de determinadas variables instruccionales más cercanas a la práctica educativa podría ayudar a entender estas diferencias. Una de esas variables instruccionales podría ser el libro de texto y el tipo de actividades y problemas que en ellos se encuentren. En este sentido, los PAV cobran una especial relevancia.
Qué son los Problemas Aritméticos Verbales
Los PAV son descripciones verbales de situaciones en las que se plantea una o varias preguntas cuyas respuestas pueden obtenerse aplicando operaciones aritméticas a los datos numéricos del problema (Verschaffel et al., 2020). Los PAV pueden entrañar diferentes niveles de dificultad para los alumnos. Uno de los aspectos más influyentes en el nivel de dificultad de un PAV es su estructura semántico-matemática (Carpenter y Moser, 1984; Greer, 1992; Vergnaud, 1991). Por ejemplo, los PAV de estructura aditiva (aquellos que pueden resolverse sumando o restando) pueden categorizarse como problemas de cambio, comparación, combinación e igualación (Carpenter y Moser, 1984; Heller y Greeno, 1978). En función del conjunto desconocido y de las relaciones (aditivas o sustractivas) existentes entre los conjuntos pueden establecerse las subcategorías descritas en el Gráfico I.
GRÁFICO I. Tipos de estructuras semántico-matemáticas aditivas
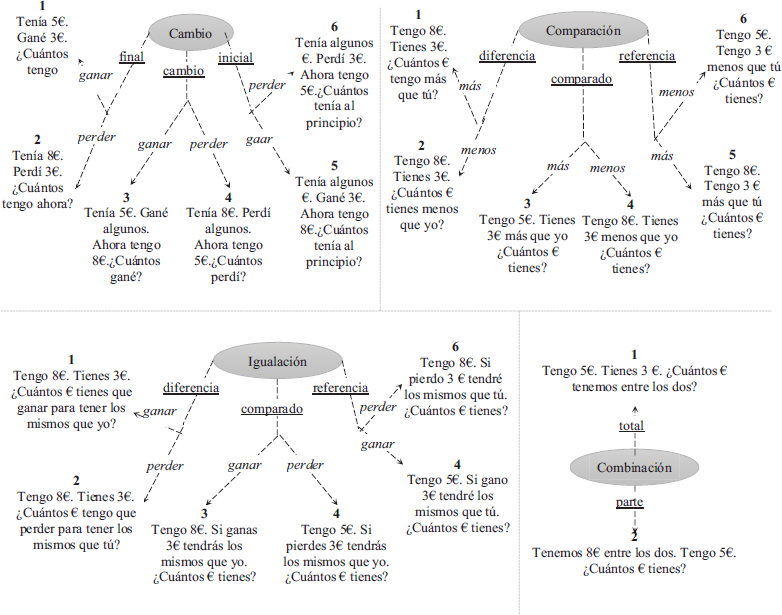
Fuente: Vicente et al. (2022). Elaboración propia.
Algunos de estos problemas podrían resolverse de una manera rutinaria. Por ejemplo, el problema de Cambio 2 del Gráfico I puede resolverse utilizando la “estrategia de la palabra clave” (Hegarty et al., 1995), tomando los datos del problema, y la expresión “perdí” como clave para restar, sin comprender su estructura matemática. Sin embargo, los problemas difíciles solo pueden resolverse comprendiendo las relaciones entre las cantidades (Verschaffel et al., 2000). Por ejemplo, para resolver el problema de Comparación 5 del Gráfico I, es necesario comprender que, si tengo más dinero que tú, tú tendrás menos que yo, y por lo tanto hay que restar, aunque la expresión “más que” sugiera que hay que sumar.
De manera similar, en los PAV de estructura multiplicativa se han distinguido cuatro tipos (Greer, 1992; Vergnaud, 1991): razón (o grupos iguales), comparación multiplicativa (o escalares), producto cartesiano y matriz rectangular. Dependiendo de la operación requerida para resolver el PAV y del conjunto desconocido, se pueden establecer las subcategorías que se muestran en el Gráfico II.
GRÁFICO II. Tipos de estructuras semántico-matemáticas multiplicativas
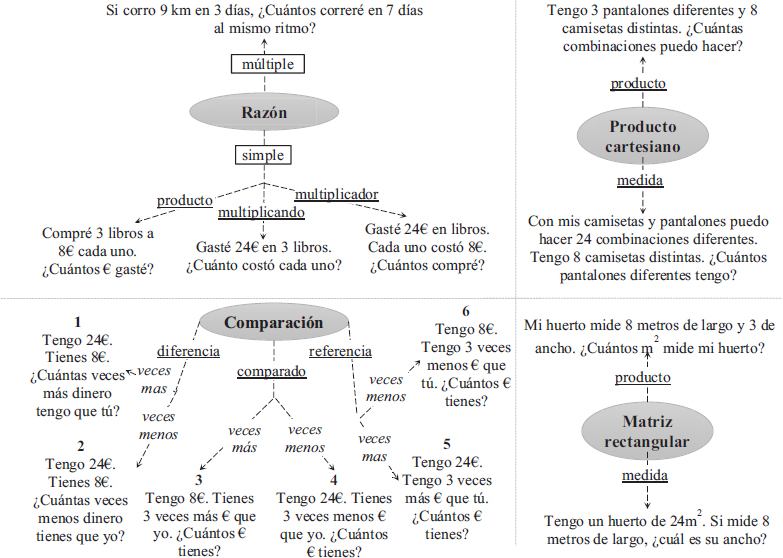
Fuente: Vicente et al. (2022). Elaboración propia.
Puesto que se han descrito 34 estructuras semántico-matemáticas para los PAV de estructuras aditivas o multiplicativas, y que la falta de práctica con algunos tipos de problemas parece dificultar su aprendizaje (Siegler y Oppenzato, 2021), los alumnos necesitan enfrentarse a la mayor variedad posible de problemas para aprender a resolverlos. De hecho, TIMSS incluye problemas de diferentes estructuras y niveles de dificultad en sus evaluaciones (I.N.E.E., 2016). Siendo esto así, un análisis de los libros de texto puede aportar información relevante sobre la variedad de problemas a la que se enfrentan los alumnos en clase de matemáticas.
Libros de Texto y Resolución de Problemas
El libro de texto se considera un recurso didáctico muy influyente en el aprendizaje escolar por tres motivos. Primero, porque lo utilizan la gran mayoría de profesores (el 94% de los docentes de los países pertenecientes a la Organización para la Cooperación Económica y el Desarrollo, Mullis et al., 2008). En España, el 81,3% de los profesores reconocen emplearlo a diario (ANELE, 2014); otros estudios informan de un uso mayor en comunidades autónomas como Madrid (97.14%, Fernández et al., 2013) o el País Vasco (96%, Mullis et al., 2008). En segundo lugar, porque traduce el currículo oficial a una secuencia de acciones concretas que profesores y alumnos pueden seguir, actuando como mediador entre el currículo oficial y el implementado (Valverde et al., 2002), y determinando en gran medida lo que se enseña en el aula (Oates, 2014). En tercer lugar, porque influyen en el aprendizaje de los alumnos; en relación con las matemáticas, los alumnos son más competentes en los contenidos a los que los libros dedican más espacio (Schmidt et al., 2001), más ejercicios y más problemas (Törnroos, 2005); y aprenden mejor los principios aritméticos y utilizan con más frecuencia las estrategias de resolución de problemas que más aparecen en los libros (Fagginger et al., 2016; Sievert et al., 2019, 2021). En cambio, los alumnos son poco competentes resolviendo determinados problemas de fracciones y decimales que, siendo matemáticamente simples, apenas aparecen en los libros (Siegler y Oppenzato, 2021).
Algunas variables específicas de los libros de texto pueden influir en el rendimiento de los alumnos, como determinados factores socio-económicos (p.e., el tipo de centro), el soporte (digital o papel) o el diseño de aspectos clave del libro, como la distribución de las tareas (Behnke, 2018). En relación con la resolución de problemas, algunos estudios han mostrado que los libros de países orientales como Japón, China o Singapur (cuyos alumnos han demostrado un elevado nivel de competencia matemática) contienen una distribución más diversificada y equilibrada de PAV aditivos y multiplicativos que los de países como Estados Unidos (Schoenfeld, 1991; Stigler et al., 1986; Xin, 2007) y España (Orrantia et al., 2005; Tárraga et al., 2021; Vicente et al., 2018), cuyos alumnos son menos competentes.
En resumen, los programas de evaluación de rendimiento matemático como TIMSS muestran las diferencias de rendimiento en matemáticas y resolución de problemas existentes entre los alumnos de diferentes contextos geográficos y culturales. Estas diferencias podrían deberse, en parte, a los libros de texto, puesto que los profesores los utilizan muy frecuentemente, y los alumnos aprenden mejor los contenidos que más aparecen en ellos. Por ello, para aprender a resolver PAV de diferentes niveles de dificultad los alumnos necesitarían libros que incluyeran una cantidad y una variedad amplia de problemas. De hecho, los libros de algunos países, cuyos alumnos han mostrado una mayor habilidad para resolver problemas, incluyen PAV más variados y de mayor dificultad que los libros de otros países, cuyos alumnos parecen ser menos competentes. De este modo, sería interesante analizar las diferencias existentes en los libros más utilizados en dos comunidades autónomas españolas, cuyos alumnos han mostrado niveles de competencia matemática muy dispares (CyL y Andalucía), en relación con los libros más utilizados en cada comunidad, y con la presencia y variedad de estructuras semántico-matemáticas de los PAV incluidos en esos libros.
El Presente Trabajo
Se pretende responder a la pregunta de si existen diferencias en los PAV incluidos en los libros más utilizados en las aulas de Primaria de CyL y Andalucía, mediante dos estudios diferentes. En el primer estudio se comprobará si los libros de texto más utilizados en las aulas de 3º de Educación Primaria1 en CyL son diferentes a los más utilizados en Andalucía. En el segundo estudio se comprobará si existen diferencias en los PAV de los distintos libros de acuerdo con tres aspectos: a) porcentaje de actividades destinadas a resolver PAV frente a otras actividades matemáticas; b) variedad de estructuras semántico-matemáticas; y c) porcentaje de problemas según su nivel de dificultad semántico-matemática.
Diseño y metodología
Muestra
El universo del estudio 1 estaba compuesto por los libros de matemáticas utilizados en las clases de 3º de Primaria de los centros públicos y concertados de CyL (851) y Andalucía (2460), durante el curso 2020-2021. Se identificaron los libros de 709 centros de CyL (83.31% del total) y de 2425 de Andalucía (98.57%). Para el estudio 2 se seleccionaron los libros que, siendo los más utilizados en cada comunidad autónoma, se emplearan en conjunto en, al menos, el 80% de los centros de cada comunidad.
Procedimiento
En el estudio 1 se determinaron los libros que se utilizaban en CyL consultando las páginas web de todos los centros de Educación Primaria de la comunidad, disponibles en la web de la Consejería de Educación. Aquellos centros que no publicaron el listado de libros en su web fueron contactados por correo electrónico. En el caso de Andalucía, los libros estaban publicados en la web de la Consejería de Educación. Después se calculó el porcentaje del total de centros en los que se utilizaba cada libro en cada comunidad autónoma. Para preservar la privacidad de las editoriales, se codificó el nombre de cada editorial con una combinación de dos números, el primero referido a la editorial, y el segundo al proyecto editorial. Posteriormente se realizó una segunda codificación de los libros más frecuentes en cada comunidad autónoma, que representara el orden que ocupa respecto a su porcentaje de uso. Para CyL se asignaron letras correlativas, y números en el caso de Andalucía. Los libros utilizados en ambas comunidades fueron codificados con una combinación de letra y número. Esta segunda codificación fue la utilizada para el estudio 2.
En relación con el estudio 2, primero se analizaron todas las actividades de los libros, entendiendo como “actividad” una tarea o conjunto de tareas agrupadas bajo un mismo epígrafe, en las que el alumno debía responder a una o varias preguntas que requerían cálculos o la aplicación de conocimientos matemáticos. Cada actividad se categorizó como: a) resolución de PAV; o b) otras actividades (en adelante OAs). Se categorizaron como actividades de resolución de PAV aquellas que incluían uno o varios PAV, considerándose PAV aquellas tareas en las que: a) se realizaba una descripción verbal de situaciones reales o imaginarias y se planteaba una pregunta matemática que se respondía aplicando al menos una de las cuatro operaciones aritméticas básicas; y b) podían clasificarse en alguna de las estructuras descritas en los Gráficos I y II. Se consideraron OAs el resto de actividades, incluyendo otros tipos de problemas verbales (p.e., estadísticos, geométricos) no clasificables en ninguna de las estructuras semántico-matemáticas de nuestro estudio. Se identificaron 8105 actividades, de las cuales 2057 fueron actividades de resolución de PAV, que incluyeron 3834 PAV.
En segundo lugar, se analizó la variedad de estructuras semántico-matemáticas. Se utilizaron clasificaciones diferentes para analizar las estructuras aditivas y multiplicativas; los primeros se clasificaron como problemas de cambio, comparación, combinación e igualación (Carpenter y Moser, 1984; Heller y Greeno, 1978), estableciéndose 20 subcategorías diferentes según el conjunto desconocido y las relaciones aditivas o sustractivas que se establecieran entre las cantidades del problema (ver Gráfico I). Los PAV de estructura multiplicativa se clasificaron como problemas de razón (o grupos iguales), comparación (o escalares), producto cartesiano y matriz rectangular (Greer, 1992; Vergnaud, 1991), estableciéndose 14 subcategorías diferentes (ver Gráfico II).
Finalmente, se categorizó cada estructura respecto al nivel de dificultad semántico-matemática, siguiendo el modelo de estrategias de resolución de Riley y Greeno (1988) para las estructuras aditivas, y los planteamientos de Greer (1992) y Vergnaud (1991) para las multiplicativas. Se consideraron fáciles las estructuras aditivas de cambio 1 y 2, comparación 1 y 2, igualación 1 y 2, y combinación 1; y las estructuras multiplicativas de razón simple, ya que son los más próximas a las de estructura aditiva (pueden llegar a resolverse como sumas o restas repetidas). Se consideraron de dificultad media las estructuras aditivas de cambio 3 y 4, comparación 3 y 4, igualación 5 y 6 y combinación 2 (ver Riley y Greeno, 1988, para las estructuras de combinación 2); y las multiplicativas de razón múltiple y las de comparación multiplicativa consistente, es decir, en las que los términos del problema ‘veces más’ o ‘veces menos’ coincidiera con la operación necesaria para resolverlo (una multiplicación y una división, respectivamente, ver Xin, 2007). Finalmente, se consideraron difíciles las estructuras aditivas de cambio 5 y 6, comparación 5 y 6, y de igualación 3 y 4, y las multiplicativas de comparación inconsistente, matriz rectangular y producto cartesiano.
Codificación y análisis de datos
Los autores codificaron conjuntamente 10 unidades didácticas de diferentes libros, para establecer los criterios de categorización. Después, dos de los autores analizaron otras 10 unidades didácticas, tras lo cual se calculó el acuerdo inter-jueces utilizando el coeficiente de Kappa de Cohen, obteniéndose índices de correlación altamente significativos (κ =.98 para la clasificación de actividades de resolución de PAV y OAs; κ =.96 para las estructuras semántico-matemáticas de los PAV). Los dos primeros autores analizaron las estructuras de los PAV del resto de la muestra, y los tres últimos, categorizaron las actividades como PAV u OAs.
Respecto a las medidas utilizadas, para el estudio 1 se calculó el porcentaje de uso de cada editorial en cada comunidad autónoma. Para el estudio 2 se calcularon dos medidas. Primero, para cada variable, se calculó una medida ponderada de las frecuencias observadas en los libros según el porcentaje de uso en cada comunidad autónoma, mediante la siguiente fórmula:
donde MCA es la medida ponderada de los libros de una comunidad autónoma concreta, F es la frecuencia absoluta de cada libro en esa variable y P es el porcentaje de uso de ese libro en esa comunidad autónoma. Aunque esta medida implica una ligera sobreestimación de las frecuencias observadas en los libros andaluces (la suma de los porcentajes de uso es ligeramente superior en Andalucía que en C&L), esto no afecta a la validez de los resultados.
La segunda medida del estudio 2 fue la frecuencia observada en cada variable, en cada libro. Esta medida permitió realizar comparaciones entre todos los libros. Para facilitar la interpretación de los resultados, se calcularon los porcentajes correspondientes a cada frecuencia observada.
Para comprobar la significatividad estadística de las diferencias encontradas, en todos los análisis se utilizó el estadístico no paramétrico Chi-cuadrado para analizar las diferencias globales, a través de tablas planificadas, y el estadístico exacto de Fisher cuando el cálculo de Chi-cuadrado no era apropiado. Para verificar el efecto de esas diferencias se utilizó el estadístico V de Cramer el cual, de acuerdo con Cohen (1988), indica si el efecto de las diferencias es pequeño (.1), mediano (.3) o grande (.5). Para comparar las diferencias entre libros concretos se utilizaron pruebas z con un nivel de significatividad de .05, utilizando comparaciones por pares de proporciones de columna de las tablas planificadas.
Hipótesis
En el estudio 1, de acuerdo con el marco teórico presentado, si los libros influyen en las diferencias de rendimiento en resolución de PAV entre los alumnos de CyL y Andalucía, los libros más utilizados en las clases de matemáticas de 3º de Primaria de CyL serán diferentes a los más utilizados en Andalucía (hipótesis 1).
En el Estudio 2, considerando los resultados de estudios previos sobre la influencia de los libros en el aprendizaje de las matemáticas, y las diferencias en las puntuaciones en TIMSS de los estudiantes castellano-leoneses y andaluces, cabría esperar que los libros más utilizados en CyL, comparados con los más utilizados en Andalucía, presentaran varias de las siguientes diferencias:
a) Un mayor porcentaje de actividades de resolución de PAV (hipótesis 2a).
b) Una mayor variedad de estructuras semántico-matemáticas (hipótesis 2b).
c) Un mayor porcentaje de PAV de estructuras de dificultad semántico-matemática media y alta, tanto aditivas (hipótesis 2c1) como multiplicativas (hipótesis 2c2).
Resultados
Estudio 1
En CyL se utilizaron 46 libros de 16 editoriales, mientras que en Andalucía se utilizaron 15 libros de 8 editoriales. Los libros más frecuentes en CyL fueron diferentes a los más utilizados en Andalucía, confirmándose la hipótesis 1. No se encontró una asociación significativa entre los libros utilizados en ambas comunidades autónomas (p <.001), siendo grande el tamaño de la diferencia (.81). En CyL los más utilizados fueron 1-1 (30.97%); 1-2 (12.78%); 2-1 (13.35%); y 3-1 (14.48%). En cambio, en Andalucía los libros más frecuentes fueron: 1-2 (26.18%); 1-3 (9.6%); 2-2 (31.92%); 3-2 (11.91%); y 4-2 (8.08%). Asimismo, el porcentaje de uso en CyL de 1-1, 2-1 y 3-1 fue mayor que en Andalucía; en cambio, en Andalucía se utilizaron con más frecuencia los libros 2 y 3 de las editoriales 1 y 2, y los libros 3-2, 4-2 y 6-1 (ver Tabla I).
TABLA I. Frecuencias y porcentajes de uso de los libros más utilizados en 3º de Primaria en los centros de CyL y Andalucía
EDITORIAL |
LIBRO |
CyL |
ANDALUCÍA |
Código Estudio 2 |
||
N |
% |
N |
% |
|||
1 |
1-1 |
218 |
30.97* |
0 |
0 |
A |
1-2 |
90 |
12.78 |
635 |
26.19* |
D2 |
|
1-3 |
11 |
1.56 |
233 |
9.61* |
J4 |
|
1-4 |
7 |
1 |
0 |
0 |
|
|
Total |
326 |
46.31 |
868 |
35.80 |
|
|
2 |
2-1 |
94 |
13.35* |
0 |
0 |
C |
2-2 |
31 |
4.40 |
774 |
31.92* |
E1 |
|
2-3 |
17 |
2.41 |
122 |
5.03* |
|
|
Otros |
4 |
0.56 |
0 |
0 |
|
|
Total |
146 |
20.72 |
896 |
36.95 |
|
|
3 |
3-1 |
102 |
14.49* |
0 |
0 |
B |
3-2 |
34 |
4.83 |
289 |
11.92* |
F3 |
|
Otros |
6 |
0.85 |
0 |
0 |
|
|
Total |
142 |
20.17 |
289 |
11.92 |
|
|
4 |
4-1 |
20 |
2.84 |
0 |
0 |
|
4-2 |
18 |
2.56 |
196 |
8.08* |
G5 |
|
Otros |
6 |
0.85 |
0 |
0 |
|
|
Total |
44 |
6.25 |
196 |
8.08 |
|
|
5 |
Sin especificar |
1 |
0.14 |
55 |
2.27* |
|
Otros |
6 |
0.86 |
0 |
0 |
|
|
Total |
7 |
1 |
55 |
2.27 |
|
|
6 |
6-1 |
1 |
0.14 |
118 |
4.87* |
|
6-2 |
7 |
1 |
0 |
0 |
|
|
Total |
8 |
1.13 |
118 |
4.87 |
|
|
7 |
7-1 |
8 |
1.14 |
0 |
0 |
|
OTRAS EDITORIALES |
17 |
1.72* |
3 |
0.11 |
|
|
SIN LIBROS |
11 |
1.56* |
0 |
0 |
|
|
TOTAL |
709 |
100 |
2425 |
100 |
|
|
Fuente: Elaboración propia.
Nota. En “Otras editoriales” se incluyeron los libros de aquellas editoriales con frecuencias absolutas menores que 5 o porcentajes inferiores al 0.7 del total de cada comunidad. El asterisco indica las diferencias estadísticamente significativas.
Considerando los resultados del estudio 1, para el estudio 2 se seleccionaron los 5 libros más utilizados en cada comunidad autónoma. Esos libros se codificaron siguiendo el procedimiento anteriormente descrito (ver Tabla I). Cabe destacar que dos libros frecuentemente utilizados en Andalucía (4-2 y 1-3) también se utilizaron en CyL aunque no se encontraran entre las cinco editoriales más utilizadas en esa comunidad, por lo que también se incluyeron en el estudio 2. Dado que esos dos libros fueron la 10ª y la 7ª editoriales más utilizadas en CyL, respectivamente, fueron codificados con la 10ª y la 7ª letra (“J” y “G”).
Estudio 2
Porcentaje de actividades de resolución de PAV
La frecuencia ponderada de actividades dedicadas a resolver PAV en los libros de CyL fue de 262, y de 693 a OAs (un 27.4% y un 72.6%, respectivamente). En los libros de Andalucía se observó una frecuencia ponderada de 207 tareas de resolución de PAV y de 654 OAs (un 24% y un 76%, respectivamente). Aunque la distribución de las tareas en los libros de ambas comunidades fue diferente -las actividades dedicadas a resolver PAV representaban un mayor porcentaje en los libros de CyL- esa diferencia no llegó a alcanzar la significatividad estadística.
No obstante, la distribución de tareas dedicadas a resolver PAV y OAs sí fue diferente en los distintos libros analizados, χ2 (7, n = 8105) = 42.74, p <.01, aunque el efecto fue pequeño (.07). Los libros A y B (los más utilizados en CyL) dedicaron un mayor porcentaje de actividades a resolver PAV; de hecho, esta diferencia fue significativa respecto al libro E1, el más utilizado en Andalucía (ver Tabla II). Asimismo, en los dos libros más frecuentes en CyL se encontraron frecuencias mayores de las esperadas, mientras que en el más frecuente de Andalucía se encontró una frecuencia menor de la esperada. Otros libros frecuentes en Andalucía, como J4 y G5, también incluyeron menos actividades de resolución de PAV que A, y frecuencias menores de las esperadas. Estos resultados confirman la hipótesis 2a. Finalmente, resulta llamativa la diferencia del total de tareas entre los diferentes libros, especialmente entre los libros A, y F3 y J4.
TABLA II. Frecuencias y porcentajes de actividades de resolución de PAV y OAs por editorial.
LIBRO |
PAV |
OAs |
N TOTAL |
||||
N |
Res.Est. |
% |
N |
Res.Est. |
% |
||
A |
383 |
7.85 |
29.6E1. J4.G5. |
911 |
5.64 |
70.4 |
1294 |
B |
289 |
1.99 |
27.9E1 |
748 |
-0.29 |
72.1 |
1037 |
C |
269 |
0.74 |
24 |
850 |
3.42 |
76 |
1119 |
D2 |
307 |
3.11 |
28.3E1.J4 |
776 |
0.73 |
71.7 |
1083 |
E1 |
216 |
-2.56 |
20.7 |
829 |
2.65 |
79.3A.B.D2 |
1045 |
F3 |
195 |
-3.87 |
26 |
556 |
-7.27 |
74 |
751 |
J4 |
150 |
-6.68 |
21.6 |
546 |
-7.64 |
78.4A.D2 |
696 |
G5 |
248 |
-0.57 |
23 |
832 |
2.76 |
77A |
1080 |
Fuente: Elaboración propia. Nota: Res.Est. = residuo estandarizado
Variedad de estructuras semántico-matemáticas
La frecuencia ponderada de estructuras de los libros castellano-leoneses y andaluces fue muy similar (17.44 y 19.18, respectivamente); de hecho, la diferencia en la distribución de esas estructuras en los libros de una y otra comunidad autónoma no fue significativa. Tampoco se encontraron diferencias significativas en la distribución de las estructuras entre los libros, ni en las comparaciones realizadas entre pares de libros (ver Gráfico III), por lo que los resultados no confirman la hipótesis 2b.
GRÁFICO III. Número de estructuras semántico-matemáticas incluidas por cada libro
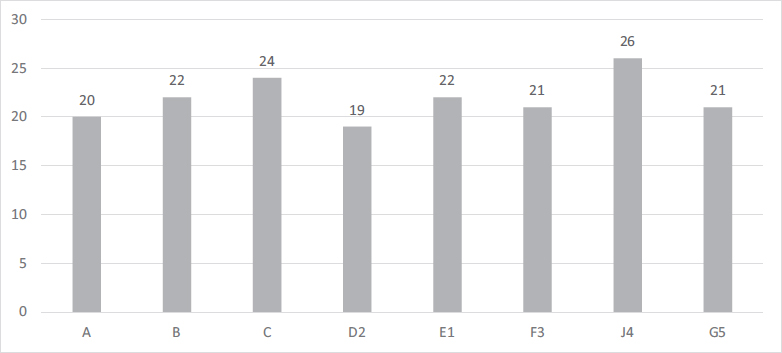
Fuente: elaboración propia
Nivel de dificultad semántico-matemática. Estructuras aditivas
La distribución de las frecuencias ponderadas de los tres niveles de dificultad fue muy similar en los libros de ambas comunidades, no encontrándose diferencias significativas. Los libros de CyL incluyeron más estructuras fáciles y de dificultad media, si bien los porcentajes que representaban respecto al total eran prácticamente idénticos (ver Gráfico IV).
GRÁFICO IV. Frecuencias y porcentajes de estructuras aditivas por nivel de dificultad semántico-matemática, ponderadas por comunidad autónoma
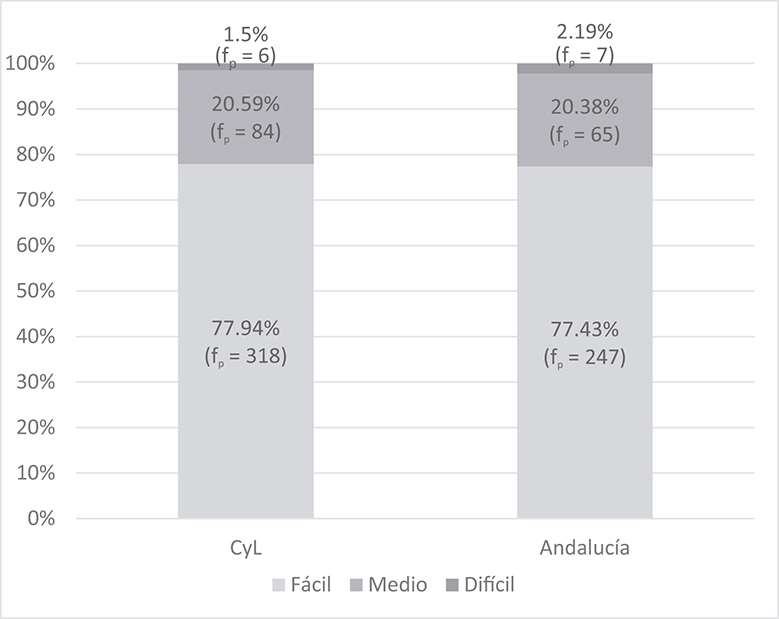
Fuente: Elaboración propia.
La comparación entre los diferentes libros mostró que la gran mayoría de las estructuras aditivas fueron fáciles, mientras que las estructuras difíciles fueron muy escasas, salvo en el libro J4. La distribución de los niveles de dificultad en los distintos libros fue significativamente diferente entre ellos (p <.001), aunque el tamaño de esta diferencia fue pequeño (.16). No hubo diferencias significativas entre las editoriales más frecuentes en CyL y Andalucía (ver Tabla III). Las únicas diferencias significativas encontradas fueron las siguientes: a) los libros A, D2 y G5 incluyeron más problemas fáciles que B y J4, aunque solo en A y D2 se encontraron frecuencias mayores a las esperadas; b) el libro B incluyó más estructuras de dificultad media que A (aunque el residuo estandarizado de A fue mayor) y G5, donde se encontró una frecuencia muy por debajo de lo esperado (al igual que F3). Finalmente, respecto a las estructuras difíciles, el libro J4 incluyó más problemas difíciles que el resto, con una frecuencia muy por encima de lo esperado, mientras que el libro C incluyó más problemas difíciles que A. Estos resultados no confirman la hipótesis 2c1.
TABLA III: Frecuencias y porcentajes de estructuras aditivas de cada nivel de dificultad semántico-matemática por libro
LIBRO |
FACIL |
MEDIO |
DIFÍCIL |
N TOTAL |
||||||
N |
Res.Est. |
% |
N |
Res.Est. |
% |
N |
Res.Est. |
% |
||
A |
584 |
18.13 |
79.9B.J4 |
141 |
7.77 |
19.3 |
6 |
-1.48 |
0.8 |
731 |
B |
227 |
-3.19 |
68.8 |
92 |
2.08 |
27.9A.G5 |
11 |
0.03 |
3.3 |
330 |
C |
164 |
-6.95 |
77.4 |
40 |
-3.96 |
18.9 |
8 |
-0.88 |
3.8A |
212 |
D2 |
451 |
10.19 |
78.8B.J4 |
117 |
4.98 |
20.5 |
4 |
-2.09 |
0.7 |
572 |
E1 |
226 |
-3.25 |
76.6 |
65 |
-1.06 |
22 |
4 |
-2.09 |
1.4 |
295 |
F3 |
132 |
-8.86 |
77.6 |
34 |
-4.66 |
20 |
4 |
-2.09 |
2.4 |
170 |
J4 |
248 |
-1.93 |
69.3 |
67 |
-0.82 |
18.7 |
43 |
9.72 |
12.0A.B.C.D2.E1.F3.G5 |
358 |
G5 |
211 |
-4.14 |
82.7B.J4 |
37 |
-4.31 |
14.5 |
7 |
-1.18 |
2.7 |
255 |
Fuente: elaboración propia.
Nota: Res.Est. = residuo estandarizado.
Nivel de dificultad semántico-matemática. Estructuras multiplicativas
De nuevo, las frecuencias ponderadas de los tres niveles de dificultad se distribuyeron de manera muy similar en los libros de ambas comunidades, sin que existieran diferencias significativas entre ambas distribuciones. Tal y como se muestra en el Gráfico V, en los libros de CyL se observó una frecuencia ponderada mayor de los tres niveles de dificultad que en los andaluces, aunque representaban prácticamente los mismos porcentajes respecto al total.
GRÁFICO V. Frecuencias y porcentajes de estructuras multiplicativas por nivel de dificultad semántico-matemática, ponderadas por comunidad autónoma
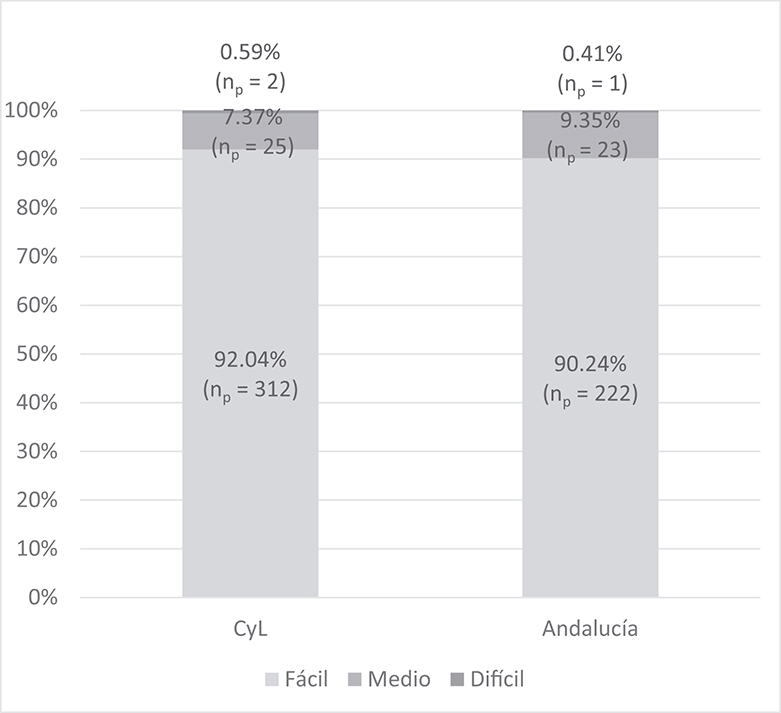
Fuente: Elaboración propia.
Respecto a la comparación entre los diferentes libros, todos mostraron una inmensa mayoría de estructuras fáciles y muy pocas estructuras difíciles. No obstante, la distribución de los niveles de dificultad fue diferente entre los libros analizados (p <.001), siendo pequeño el tamaño de esa diferencia (.14). No se encontraron diferencias significativas entre los libros más frecuentes en CyL y Andalucía (ver tabla IV). Se encontraron las siguientes diferencias: en primer lugar, los libros A y D2 –los dos con frecuencias muy por encima de lo esperado- incluyeron más estructuras fáciles que B, E1, F3 y J4; además, C y G5 incluyeron más estructuras fáciles que B y J4, siendo este último el que obtuvo una frecuencia más alejada de lo esperado. En segundo lugar, J4 incluyó más estructuras de dificultad media que el resto excepto B y E1, aunque su diferencia respecto al valor esperado fue menor que B; además, B y E1 también incluyeron más estructuras de dificultad media que A, C, D2 y G5, siendo esta última la que se quedó más lejos –por debajo- del valor esperado. Tomados en conjunto, estos resultados no confirman la hipótesis 2c2.
TABLA IV: Frecuencias y porcentajes de estructuras multiplicativas de cada nivel de dificultad semántico-matemática por libro.
LIBRO |
FACIL |
MEDIO |
DIFÍCIL |
N TOTAL |
||||||
N |
Res.Est. |
% |
N |
Res.Est. |
% |
N |
Res.Est. |
% |
||
A |
522 |
15.47 |
94.2B.E1.F3.J4 |
32 |
1.15 |
5.8 |
0 |
-1.55 |
0 |
554 |
B |
267 |
-0.09 |
84.8 |
43 |
3.31 |
13.7A.C.D2.G5 |
5 |
1.68 |
1.6 |
315 |
C |
248 |
-1.25 |
93.6B.J4 |
13 |
-2.56 |
4.9 |
4 |
1.03 |
1.5 |
265 |
D2 |
440 |
10.47 |
93.8B. E1.F3.J4 |
29 |
0.57 |
6.2 |
0 |
-1.55 |
0 |
469 |
E1 |
186 |
-5.03 |
86.5 |
29 |
0.57 |
13.5A.C.D2.G5 |
0 |
-1.55 |
0 |
215 |
F3 |
169 |
-6.07 |
86.2 |
23 |
-0.61 |
11.7 |
4 |
1.03 |
2 |
196 |
J4 |
113 |
-9.49 |
76.4 |
31 |
0.96 |
20.9A.C.D2.G5 |
4 |
1.03 |
2.7 |
148 |
G5 |
203 |
-4.00 |
94.9B.J4 |
9 |
-3.35 |
4.2 |
2 |
-0.26 |
0.9 |
214 |
Fuente: Elaboración propia. Nota. Res.Est. = residuo estandarizado
Discusión
Según los resultados de TIMSS (I.N.E.E., 2016), los alumnos de CyL obtienen mejores puntuaciones en la prueba de matemáticas que los andaluces, por lo que, de acuerdo con los marcos teóricos del propio TIMSS, serían más hábiles para resolver PAV de diferentes niveles de dificultad (Mullis et al., 2020). Esta diferencia de rendimiento, que ha sido atribuida a factores generales como diferencias en el ISEC o un sistema educativo más equitativo (I.N.E.E., 2023), también podría deberse a los libros de texto. Los libros son el recurso didáctico más utilizado por los profesores para enseñar a resolver problemas a sus alumnos en el aula (Hiebert et al., 2003; Mullis et al., 2008). Además, la variedad y el nivel de dificultad de los problemas a los que se enfrentan los niños a partir de los libros influye en su habilidad para resolverlos (Siegler y Oppenzato, 2021), siendo la estructura semántico-matemática de esos problemas una de las variables que más influye en su nivel de dificultad (Carpenter y Moser, 1984; Greer, 1992; Vergnaud, 1991). Por otra parte, algunos estudios han mostrado que los libros de países con alumnos más competentes incluyen problemas de estructuras semántico-matemáticas variadas (Schoenfeld, 1991; Stigler et al., 1986; Xin, 2007), a diferencia de los libros de otros países, como España (Orrantia et al. 2005; Tárraga et al., 2021; Vicente et al., 2018). Siendo esto así, cabría preguntarse si parte de la diferencia en el nivel de rendimiento de los alumnos de CyL y Andalucía podría atribuirse a los libros de texto utilizados en una y otra comunidad autónoma. Si existiera tal influencia, cabría esperar que los libros más utilizados en CyL fueran diferentes a los más frecuentes en Andalucía y, en ese caso, que en los libros más frecuentes en CyL se encontraran: a) un mayor porcentaje de actividades de resolución de PAV, b) una mayor variedad de estructuras semántico-matemáticas, y c) un mayor porcentaje de PAV de dificultad semántico-matemática media o alta, de acuerdo con las estructuras y niveles de dificultad descritos en la literatura (Carpenter y Moser, 1984; Greer, 1992; Riley y Greeno, 1988; Vergnaud, 1991). Cuantas más diferencias de las anteriormente señaladas concurran, mayor influencia cabría atribuirle al diseño de los libros en las diferencias de rendimiento de los alumnos castellano-leoneses y andaluces.
Los resultados del estudio 1 han mostrado que en CyL y Andalucía se utilizan libros diferentes. No obstante, de las tres medidas consideradas en el estudio 2 para analizar los PAV de esos libros, solo el porcentaje de actividades dedicadas a resolver PAV apunta a que los libros más utilizados en CyL son más adecuados que los de Andalucía para que los alumnos aprendan a resolver problemas. Si, además del porcentaje, tenemos en cuenta que la cantidad de actividades dedicadas a resolver PAV de los libros más utilizados en CyL es mucho mayor que en los de Andalucía (más del doble, en algunos casos), podría concluirse que esa práctica más intensa en resolución de problemas podría ser determinante. De estos resultados se desprende que podría no ser necesario un porcentaje elevado de problemas con dificultad media o alta (los libros más utilizados en CyL no incluyeron una variedad significativamente mayor de estructuras semántico-matemáticas, ni más problemas de dificultad semántico-matemática media o alta), pero sí mucha práctica con problemas fáciles y solo en algunos casos PAV más complejos. Estos resultados matizan los obtenidos en estudios previos que comparaban los problemas de los libros de diferentes países (Orrantia et al., 2005; Schoenfeld, 1991; Stigler et al., 1986; Tárraga et al., 2021; Xin, 2007), y coinciden en parte con los de Vicente et al. (2022) al comparar libros españoles con los de Singapur. Estos autores encontraron que los libros de Singapur contenían una mayor proporción de actividades de resolución de PAV que los españoles, y también problemas más difíciles, si bien el efecto de esta última diferencia era pequeño. En los libros singapurenses, al igual que en los analizados en nuestro estudio, la gran mayoría de los problemas eran fáciles. Las diferencias entre los libros de ambos países parecen residir en las ayudas al razonamiento que proporcionan a los alumnos, como el uso de representaciones gráficas (Kaur, 2015; Vicente, 2022), modelos de resolución más completos y basados en el razonamiento (Vicente et al., 2020) o un mayor nivel de autenticidad de los problemas (Vicente et al., 2021).
Asimismo, es razonable pensar que la influencia de los libros en el rendimiento de los alumnos esté mediada por el modo en el que los profesores resuelven los problemas en clase. Existen evidencias de que solo los profesores con un mayor conocimiento para la enseñanza de resolución de problemas promueven un mayor razonamiento al resolver cualquier tipo de problema; en cambio, los profesores con bajo conocimiento tienden a evitar los problemas más difíciles (Ramos et al., 2024). Siendo esto así, aunque algunos de los libros más utilizados en Andalucía contienen más problemas de dificultad media, quizá muchos no lleguen a implementarlos en el aula porque los consideren inadecuados para sus alumnos.
Conclusiones
Los resultados del presente estudio permiten extraer tres conclusiones. Primero, aunque los libros de texto más utilizados en CyL no son los mismos que en Andalucía, todos esos libros son, en esencia, muy similares. De las tres medidas analizadas, solo el porcentaje de actividades de resolución de PAV parece marcar una diferencia clara entre los libros más utilizados en CyL y Andalucía. La ausencia de diferencias en la variedad de estructuras y niveles de dificultad semántico-matemática, tanto en los problemas aditivos como multiplicativos, llevan a pensar que la influencia de los libros en las diferencias de rendimiento de los alumnos de CyL y Andalucía parecen limitarse a una mayor cantidad de práctica con los PAV en los libros castellano-leoneses.
Una segunda conclusión es que, a pesar de que los libros más utilizados en CyL contienen PAV de un número de estructuras muy reducido y de baja dificultad semántico-matemática, parecen ser un material suficiente para que los alumnos desarrollen una habilidad para resolver problemas por encima de la media del país. Más allá de la cantidad de PAV que contienen, esto puede deberse, entre otras causas, a características de los libros no descritas en este estudio y al modo en que los maestros los utilizan en el aula.
Una tercera conclusión es que algunos libros podrían ser más adecuados que el resto para la enseñanza de determinados aspectos relacionados con los PAV, puesto que, aunque no se han encontrado grandes diferencias entre los libros más utilizados en CyL y Andalucía, sí existen diferencias entre libros concretos. Por ejemplo, mientras A o D2 proporcionan un banco amplio de problemas, y problemas de mayor nivel de complejidad procedimental, J4 presenta tanto una variedad mayor de estructuras como problemas más difíciles a nivel semántico-matemático (también B, para los problemas de estructuras aditivas).
Limitaciones y prospectiva
Los resultados del presente estudio deben interpretarse con cautela debido a la existencia de una serie de limitaciones. En primer lugar, la muestra de libros analizada es limitada, puesto que solo se incluyeron libros de 3º de Primaria de dos comunidades autónomas. Siendo esto así, sería recomendable realizar estudios adicionales que amplíen la muestra de libros analizados a todos los cursos de Primaria, a otras comunidades autónomas e, incluso, a otros países. De hecho, sería conveniente replicar este estudio comparando los libros de diferentes regiones de otros países. En segundo lugar, de todas las fuentes de complejidad de los problemas solo se ha considerado la dificultad semántico-matemática, dejándose al margen otras variables de los problemas, como sus características lingüísticas, su carácter estereotipado o no estereotipado, o la ubicación de la incógnita. Estas cuestiones deberían analizarse en el futuro, junto con otros aspectos de los PAV como las ayudas a la resolución o su nivel de autenticidad. En tercer lugar, se han analizado los PAV incluidos en los libros, pero no su rol dentro de la unidad didáctica. Sería interesante conocer qué papel juega el pequeño porcentaje de problemas de dificultad semántico-matemática media o alta en las unidades didácticas (p.e., como desafío al principio de la unidad didáctica, como práctica al final de esta). Por último, sería muy interesante comparar el modo en el que profesores de ambas comunidades autónomas utilizan los libros en clase (p.e., su metodología de enseñanza o el modo de evaluar los aprendizajes).
Referencias bibliográficas
ANELE. (2014). La edición de libros de texto en España. ANELE.
Behnke, Y. (2018). Textbook Effects and Efficacy. En E. Fuchs & A. Bock (Eds), The Palgrave Handbook of Textbook Studies. Palgrave Macmillan. https://doi.org/10.1057/978-1-137-53142-1_28
Carpenter, T.P., & Moser, J.M. (1984). The acquisition of addition and subtraction concepts. En R. Lesh & M. Landau (Eds.), The acquisition of mathematical concepts and processes, (pp. 7–44). Academic Press.
Cohen, J. (1988). Statistical power and analysis for the behavioral sciences. Lawrence Erlbaum Associates, Inc. https://doi.org/10.1002/bs.3830330104
Fagginger, M., Hickendorff, M., van Putten, C. Beguin, A., & Heiser, W. (2016). Multilevel latent class analysis for large-scale educational assessment data. Exploring the relation between the curriculum and students’ mathematical strategies. Applied Measurement in Education, 29(2), 144–159. https://doi.org/10.1080/08957347.2016.1138959
Fernández, P., Caballero, P., & Fernández, J. (2013). ¿Yerra el niño o yerra el libro de Matemáticas? Números. Revista de Didáctica de las Matemáticas, 83, 131-148.
Greer, B. (1992). Multiplication and division as models of situations. En D.A. Grouws (Ed.), Handbook of research on mathematics teaching and learning, (pp. 276–295). Macmillan.
Hegarty, M., Mayer, R.E., & Monk, C.A. (1995). Comprehension of arithmetic word problems: a comparison of successful and unsuccessful problem solvers. Journal of Educational Psychology, 87, 18–32. https://doi.org/10.1037/0022-0663.87.1.18
Heller, J., & Greeno, J. (1978). Semantic processing in arithmetic word problem solving. Comunicación presentada en la Midwestern Psychological Association Convention, Chicago.
Hiebert, J., Gallimore, R., Givvin, K.B., Hollingsworth, H., Jacobs, J., Chui, A.M. et al. (2003). Teaching mathematics in seven countries. Results from the TIMSS 1999 Video Study. National Center for Education Statistics (NCES).
Hippe, R., Jakubowski, M., & Araújo, L. (2018). Regional inequalities in PISA: the case of Italy and Spain. Publications Office of the European Union. https://doi.org/10.2760/495702
Instituto Nacional de Evaluación Educativa (2016). TIMSS 2015. Estudio internacional de tendencias en Matemáticas y Ciencias. (Informe español: resultados y contexto). Ministerio de Educación, Cultura y Deporte. https://sede.educacion.gob.es/publiventa/descarga.action?f_codigo_agc=18230
Instituto Nacional de Evaluación Educativa (2023). PISA 2022. Programa para la evaluación Internacional de los estudiantes. Informe español. Ministerio de Educación, Formación Profesional y Deportes. https://www.libreria.educacion.gob.es/ebook/184935/free_download/
Kaur, B. (2015). The model method: A tool for representing and visualizing relationships. En X. Sun, B. Kaur & J. Novotna (Eds.), Conference proceedings of ICMI Study 23: Primary mathematics study on whole numbers, (pp. 448–455). http://www.umac.mo/fed/ICMI23/doc/ProceedingsICMI_STUDY_23_final.pdf.
Lindquist, M., Philpot, R., Mullis, I., & Cotter, K. E. (2017). TIMSS 2019 Mathematics Framework. En I.V.S. Mullis & M.O. Martin (Eds), TIMSS 2019 Assessment Frameworks. Recuperado de: http://timssandpirls.bc.edu/timss2019/frameworks/
Mullis, I., Martin, M., & Foy, P. (2008). TIMSS 2007 international mathematics report: Findings from IEA’s Trends in International Mathematics and Science Study at the fourth and eighth grade. TIMSS and PIRLS International Study Center, Boston College. http://pirls.bc.edu/timss2007/mathreport.html
Mullis, I., Martin, M., Foy, P., Kelly, D., & Fishbein, B. (2020). TIMSS 2019 International Results in Mathematics and Science. TIMSS and PIRLS International Study Center, Boston College. https://timssandpirls.bc.edu/timss2019/international-results/
Oates, T. (2014). Why textbooks count. Cambridge assessments. http://www.cambridgeassessment.org.uk/Images/181744-why-textbooks-count-tim-oates.pdf
Orrantia, J., González, L.B., & Vicente, S. (2005). Analysing arithmetic word problems in Primary Education textbooks. Journal for the Study of Education and Development, 28(4), 429–451. https://doi.org/10.1174/021037005774518929
Philpot, R., Lindquist, M., Mullis. I.V.S. & Aldrich, Ch. E.A. (2021). TIMSS 2023 Mathematics Framework. En I.V.S. Mullis, M.O. Martin & von Davier, M. (Eds), TIMSS 2023 Assessment frameworks. TIMSS and PIRLS International Study Center.
Ramos, M., Vicente, S., Rosales, J., & Chamoso, J. (2024). Influencia del conocimiento pedagógico del profesorado en su práctica de aula cuando resuelve problemas aritméticos verbales con su alumnado. Un estudio exploratorio. Journal for the Study of Education and Development, 47(2), 321-345. https://doi.org/10.1177/02103702241253415
Rao, N., Ng, S. S. N., & Pearson, E. (2010). Preschool pedagogy: A fusion of traditional Chinese beliefs and contemporary notions of appropriate practice. En C. Chan, & N. Rao (Eds.), Revisiting the Chinese learner. CERC studies in comparative education, (pp. 255–279). Springer. https://doi.org/10.1007/978-90-481-3840-1_9
Riley, M., & Greeno, J. (1988). Developmental analysis of understanding language about quantities of solving problems. Cognition and Instruction, 5, 49–101. https://doi.org/10.1207/s1532690xci0501_2
Schmidt, W., McKnight, C., Houang, R., Wang, H., Wiley, D., Cogan, L., et al. (2001). Why schools matter: A cross-national comparison of curriculum and learning. Bass.
Schoenfeld, A.H. (1991). On mathematics as sense-making: An informal attack on the unfortunate divorce of formal and informal mathematics. En J.F. Voss, D.N. Perkins & J.W. Segal (Eds.), Informal reasoning and education, (pp. 311–343). Lawrence Erlbaum Associates.
Siegler, R., & Oppenzato, C. (2021). Missing Input: How Imbalanced Distributions of Textbook Problems Affect Mathematics Learning. Child Development Perspectives, 15(2), 76-82. https://doi.org/10.1111/cdep.12402
Sievert, H., van den Ham, A.K., & Heinze, A. (2021). Are first graders’ arithmetic skills related to the quality of mathematics textbooks? A study on students’ use of arithmetic principles. Learning and Instruction, 71(101401), 1–14. https://doi.org/10.1016/j.learninstruc.2020.101401
Sievert, H., van den Ham, A.K., Niedermeyer, I., & Heinze, A. (2019). Effects of mathematics textbooks on the development of primary school children’s adaptive expertise in arithmetic. Learning and Individual Differences, 74(101716), 1–13.
Stigler, J., Fuson, K., Ham, M., & Kim, M. (1986). An analysis of addition and subtraction word problems in American and Soviet elementary mathematics textbooks. Cognition and Instruction, 3, 153–171.
Tárraga, R., Tarín, J., & Lacruz, I. (2021). Analysis of Word Problems in Primary Education Mathematics Textbooks in Spain. Mathematics, 9(17), 2123. https://doi.org/10.3390/math9172123
Törnroos, J. (2005). Mathematics textbooks, opportunity to learn and student achievement. Studies in Educational Evaluation, 31(4), 315–327.
Valverde, G., Bianchi, L. J., Wolfe, R., Schmidt, W. H., & Houang, R. T. (2002). According to the book: Using TIMSS to investigate the translation of policy into practice through the world of textbooks. Kluwer Academic Publishers.
Vergnaud, G. (1991). El niño, las matemáticas y la realidad. Trillas.
Verschaffel, L., Depaepe, F., & Van Dooren, W. (2020). Word problems in mathematics education. En S. Lerman (Ed.), Encyclopedia of mathematics education, (pp. 908–911). Springer.
Verschaffel, L., Greer, B., & De Corte, E. (2000). Making sense of word problems. Swets y Zeitlinger Publishers. https://doi.org/10.1023/A:1004190927303
Vicente, S., Manchado, E., & Verschaffel, L. (2018). Solving arithmetic word problems. An analysis of Spanish textbooks. Culture and Educación, 30, 71–104. https://doi.org/10.1080/11356405.2017.1421606
Vicente, S., Sánchez, R., & Verschaffel, L. (2020). Word problem solving approaches in mathematics textbooks: a comparison between Singapore and Spain. European Journal of Psychology of Education, 35, 567–587. https://doi.org/10.1007/s10212-019-00447-3
Vicente, S., Verschaffel, L., & Múñez, D. (2021). Comparación del nivel de autenticidad de los problemas aritméticos verbales de los libros de texto españoles y singapurenses. Cultura y Educación, 33(1), 106–133. https://doi.org/10.1080/11356405.2020.1859738
Vicente, S., Verschaffel, L, Sánchez, R., & Múñez, D. (2022). Arithmetic word problem solving. Analysis of Singaporean and Spanish textbooks. Educational Studies in Mathematics, 111, 375–397. https://doi.org/10.1007/s10649-022-10169-x
Xin, Y.P. (2007). Word problem solving tasks in textbooks and their relation to student performance. The Journal of Educational Research, 6, 347–359. https://doi.org/10.3200/JOER.100.6.347-360
Información de contacto: Santiago Vicente Martín. Universidad de Salamanca. Facultad de Educación. Dpto. Psicología Evolutiva y de la Educación. Paseo Canalejas 169. 37008, Salamanca. E-mail: sanvicente@usal.es
_______________________________
1 Se analizaron los libros de un único curso para que la muestra fuera abarcable, considerando el número de variables y de libros analizados. Se eligió 3º de Primaria porque en ese nivel aparecen estructuras tanto aditivas como multiplicativas, y no son frecuentes los problemas con fracciones, decimales o transformaciones de unidades de medida, que implican niveles adicionales de dificultad.