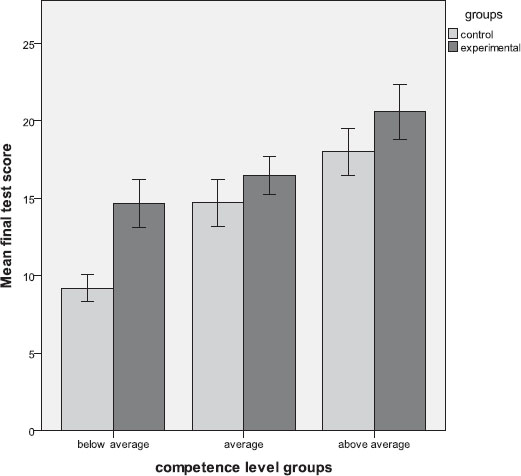
FIGURE I. The performance of below-average, average, and above-average students within the experimental and control groups. Error bars represent ±1 SE.
Source: Compiled by author
https://doi.org/10.4438/1988-592X-RE-2023-401-584
Csaba Szabó
https://orcid.org/0000-0003-4783-5411
Eötvös Loránd University, Faculty of Science
MTA-ELTE Theory of Learning Mathematics Research Group
Csilla Zámbó
https://orcid.org/0000-0002-7230-7023
Eötvös Loránd University, Faculty of Primary and Pre-School Education
MTA-ELTE Theory of Learning Mathematics Research Group
Anna Muzsnay
https://orcid.org/0000-0003-4045-0527
University of Debrecen
MTA-ELTE Theory of Learning Mathematics Research Group
Janka Szeibert
https://orcid.org/0000-0002-4267-9360
Eötvös Loránd University, Faculty of Primary and Pre-School Education
MTA-ELTE Theory of Learning Mathematics Research Group
László Bernáth
https://orcid.org/0000-0002-8314-6560
Eötvös Loránd University, Faculty of Education and Psychology
MTA-ELTE Theory of Learning Mathematics Research Group
Abstract
Retrieving information from memory can strengthen one’s memory of the retrieved information itself. The strategic use of retrieval to enhance memory and help long-term retention is known as test-enhanced learning or retrieval practice. Test-enhanced learning has been proven effective concerning different learning materials, but these experiments were primarily conducted in laboratory environments and focused mainly on memorization. Our aim was to explore the efficacy of test-enhanced learning used for teaching mathematics at university level. The experiment was carried out in classroom settings, concerning obligatory courses. The participants were six groups of undergraduate pre-service mathematics teachers. Three groups learned Number Theory using the testing effect, and the other three learned using traditional methods. The experimental and control groups learned the exact same information in the lecture and wrote the same final test. The experimental group performed significantly better than the control group, although their performance on the initial competence exams was significantly worse. The results indicate that test-enhanced learning has a significant advantage in solving complex mathematical problems. To examine the effect of differences in individual competence, we divided the students in both experimental and control groups into low-, middle-, and high-performing groups. The efficacy of test-enhanced learning was demonstrated in all the three performance levels. Regarding the three pairs of groups, members of the experimental group using test-enhanced learning performed better than those of the control group.
Keywords: testing effect retrieval practice mathematics complex problems individual differences
Resumen
Recuperar información de la memoria puede reforzar el recuerdo de la propia información recuperada. (Este es el fenómeno llamado “efecto test” o “testing effect”.) El uso estratégico de la recuperación para mejorar la memoria y ayudar a la retención a largo plazo se conoce como aprendizaje potenciado por pruebas o aprendizaje potenciado por recuperación. El aprendizaje potenciado por pruebas ha demostrado su eficacia en relación con diferentes materiales de aprendizaje, pero estos experimentos se realizaron principalmente en entornos de laboratorio y se centraron sobre todo en la memorización. Nuestro objetivo era explorar la eficacia del aprendizaje potenciado por pruebas utilizado para la enseñanza de las matemáticas a nivel universitario. El experimento se llevó a cabo en entornos de aula, en relación con cursos obligatorios. Los participantes fueron seis grupos de profesores de matemáticas en formación. Tres grupos aprendieron Teoría de los Números utilizando el efecto test, y los otros tres aprendieron utilizando métodos tradicionales. Los grupos experimental y de control aprendieron exactamente la misma información en la clase y realizaron el mismo examen final. El grupo experimental obtuvo un rendimiento significativamente mejor que el grupo de control, aunque su rendimiento en los exámenes de competencia inicial fue significativamente peor. Los resultados indican que el aprendizaje potenciado por los exámenes tiene una ventaja significativa en el aprendizaje de la resolución de problemas matemáticos complejos. Para examinar el efecto de las diferencias en la competencia individual, dividimos a los estudiantes de los grupos experimental y de control en grupos de rendimiento bajo, medio y alto. La eficacia del aprendizaje potenciado por los exámenes se demostró en los tres niveles de rendimiento. En cuanto a los tres pares de grupos, los miembros del grupo experimental que utilizó el aprendizaje potenciado por tests obtuvieron mejores resultados que los del grupo de control.
Palabras clave: efecto del test aprendizaje potenciado por recuperación matemáticas problemas complejos diferencias individuales
Retrieving information from memory after an initial learning phase enhances long-term retention more than restudying the material, an advantage referred to as the testing effect (Roediger & Butler, 2011; Rowland, 2014). The testing effect has been demonstrated with various practice tests, materials, and age groups (Karpicke, 2017) including tertiary education (Butler, 2010). However, these experiments were mostly conducted in laboratory environments concerning the memorization of texts or words. There have been only a limited number of experiments in the field of mathematics, in real-life educational environments (Lyle & Crawford, 2011; Lyle, Hopkins et al., 2016; Fazio 2019; Lyle, Bego et al., 2020).
Testing enhances the effectiveness not only of word-for-word retention - as opposed to rereading - but also of the application of the newly acquired knowledge. Smith and Karpicke (2014) have shown that groups studying with tests performed better than the control group not only in word-for-word retention tasks but also in tasks demanding the synthesis of the information within the given text. Furthermore, knowledge acquired with the use of retrieval practice was not only shown to be more applicable within the given subject of the text than rereading-based knowledge but also more easily transferable to other areas (Butler, 2010; van Eersel et al., 2016).
The strong evidence for a direct effect of testing suggests that retrieval practice may be regarded as one of the most effective learning techniques. (Karpicke & Blunt, 2011; Larsen et al., 2013; Dunlosky et al., 2013; Donoghue & Hattie, 2021). However, there are certain areas where the demonstration of the testing effect has either failed or produced contradicting results.
A potential impediment concerns the results of Khanna (2015) based on a study conducted within an introductory psychology course. Students were placed into “ungraded quiz,” “graded quiz,” and “no quiz” groups, and the first two were given six surprise tests in the semester. The results show that the “ungraded” group performed better than the other two groups, and there was no difference in performance between the “graded” and “no quiz” groups. Khanna’s explanation for this result is that higher levels of anxiety can eliminate the testing effect on the “graded” group. However, these conclusions contradict the findings of Agarwal et al., (2012) that test anxiety decreases in students studying with frequent testing and the results of Tse & Pu (2012) that demonstrated the efficiency of testing effect in case of people both with low and high anxiety. One possible solution to this contradiction is that anxiety only impairs study performance in the case of weak intrinsic motivation, and, if backed up by higher intrinsic motivation, anxiety may, in fact, serve to improve performance (Wang et al., 2015). The results of Emmerdinger and Kuhbandner (2019) can give another solution to the contradiction. They found that the testing effect appears independently of the emotional state (negative, neutral, or positive) of the participants.
Concerning the form of testing, both short-answer and multiple-choice tests are more effective ways of learning than rereading (Kang et al, McDermott, and Roediger, 2007). The efficacy of testing may vary, depending on the presence of feedback. If feedback is included, short-answer questions are more beneficial; otherwise, multiple-choice tests are more effective (Kang et al., 2007).
Another contradiction concerns the role of individual differences in test-enhanced learning. Orr and Foster (2017) conducted their examination within a biology course in which students had the option of participating in tests administered periodically throughout. Those who systematically took part in the tests performed better in the final exam than those who did not. Furthermore, most important from our viewpoint is that this advantage was observed in students with above-average, average, and below-average skills alike. By contrast, the results of Carpenter et al. (2016), also within a biology course, show that test-enhanced learning was only effective in students with above-average skills and that no enhancement was observed in students with average and below-average skills. This greatly impedes the application of test-enhanced learning in a classroom setting. Nevertheless, the results of Carpenter et al. (2016) contradict the assertion of Brewer and Unsworth (2012) that individuals with lower general-fluid intelligence (Gf-I) profited more from test-based studying than individuals with higher Gf-I and that test-enhanced learning could not be observed at all concerning the highest-level Gf-I individuals. Furthermore, Balota et al. (2006) demonstrated the benefits of testing effect among people having dementia of Alzheimer’s type. This result suggests that testing is beneficial for those with high cognitive abilities, for those with average or below average abilities, and even for memory-impaired people.
The third factor that has produced contradicting results concerns the role of the level of complexity of the object of study. Van Gog and Sweller (2015) argue that the testing effect can only be observed when there is no interaction between the items to be learned, for instance when learning the vocabulary of a foreign language; in more complex subject materials, it either diminishes or disappears completely. (However, see Karpicke and Aue (2015) for theoretical counterarguments). Leahy et al. (2015) observed the testing effect related to complex study material upon immediate retention testing, and they did not detect any effect at all following one week’s delay. A similarly negative result was arrived at by Tran et al. (2015), whose “revision” and “testing” groups had to learn consecutively appearing sentences describing various scenarios. In the final test, although the retention of the individual sentences showed the testing effect, there was no difference in performance between the two groups in terms of drawing conclusions based on the content of the sentences. In other words, they found that, in complex tasks requiring deductive thinking, the testing effect disappears. Eglington and Kang (2018) repeated the experiment of Tran et al. (2015) with one modification (the sentences were shown on the monitor all at once, not one by one); their results demonstrated the benefits of the testing effect on this deductive task.
In the study of Peterson and Wissmann (2018), the retrieval effect had no advantage compared to restudying in the case of solving complex problems requiring analogical thinking. Despite these results, Wong et al (2019) and Hostetter et al. (2019) proved the benefits of retrieval learning in analogical problem-solving. Most likely, in the case of Peterson and Wissmann (2018), the inefficacy of the retrieval effect can be explained not (or not only) by the requirement of analogical thinking, but maybe (also) by the complexity of the problems or some other elements of the experimental design. According to the abovementioned results, in tasks demanding complex or deductive thinking, the advantage of test-enhanced learning over rereading learning is unclear. Furthermore, as the results of Carpenter et al. (2016) and Brewer and Unsworth (2012) have shown, the role of individual differences in competence is also ambiguous.
Mathematical problems require developed deductive and problem-solving skills, and the problems themselves are quite complex. Developing problem-solving skills in mathematics requires the application of procedures and deep conceptual understanding, not only memorization. Although there have been only a few investigations about the testing effect on mathematical problem-solving in a real school environment, recent studies suggest that the intensive use of retrieval practice may be an effective way of learning (Lyle and Crawford, 2011; Fazio 2019; Lyle et al., 2016; Lyle et al., 2020). The paper of Avvisati and Borgonovi (2020) concerns problem-solving in mathematics. Although the environment is not a real educational environment in the sense that they measured the effect of a single test practice, their large sample investigation is relevant for us since it uses educational material. They demonstrate that the number of mathematical problems in the first test had a small positive effect on the average mathematics performance on the second test. In the experiment of Yeo and Fazio (2019), the efficacy of retrieval practice and worked examples for different learning goals were examined. The optimal learning strategy depended on the retention interval and the nature of the materials. Repeated testing was more effective than repeated studying after a 1-week delay when students’ goal was to remember the text of a worked example. On the other hand, they found that learning a novel maths procedure and measuring performance immediately, repeated studying was more optimal than repeated testing, regardless of the nature of the materials. Finally, the study of Lyle et al. (2011) is the most relevant study for our research. They incorporated retrieval practice into a course on statistics for psychology by adding a brief retrieval exercise for some essential lecture material at the end of every lecture. This method significantly and substantially increased exam scores. Students liked the retrieval practice and believed it was helpful. In Lyle’s later studies, spaced retrieval practice was investigated in the precalculus course. Their results have encouraged us to explore further aspects of the testing effect in university mathematics classes (Lyle et al. 2016, 2020).
When applying retrieval practice in a real school setting, two important questions arise: the form of testing and the differences in individuals’ mathematical competencies. Concerning the form of testing, both short-answer and multiple-choice tests are more effective ways of learning than rereading (Kang et al. 2007). The efficacy of testing may vary, depending on the presence of feedback concerning the practice test. If feedback is included, short-answer questions are more beneficial; otherwise, multiple-choice tests are more effective (Kang et al., 2007). Also, the question of differences in individuals’ mathematical competencies can be a central one. We will further discuss this aspect in the next chapter as its investigation was part of the aim of our study.
In this study, we aimed to implement retrieval practice in university education and investigate its efficacy in learning higher mathematics. When applying retrieval practice in a real school environment in mathematics, it is not evident which method to use and how to put it into practice. We must pay attention to the fact that retrieving must take place within 24 hours, there should be no copying, no cheating, it should not take a lot of time, and students should be involved in it. The form of the testing and the type of questions have to be considered, as well.
Also, our goal is to examine if the efficacy of retrieval practice depends on the individuals’ mathematical competence. In case of university maths education, this is a particularly important aspect, where differences among the entering students are usually enormous. For this reason, our study examines an actual educational environment and regularly applied course material. It compares the performance of two groups of students in an Algebra and Number Theory course studying with either a traditional method or a test-based method (recalling study material on one occasion, immediately after learning it) considering the effects of differences in individual competence. To examine the differences in individual competence, we grouped students based not on their all-around performance during the whole course, as Carpenter et al. (2016) did, but on a competence level test taken in the initial class.
The authors conducted a quasi-experimental study to figure out whether retrieval effect leads to improvement in mathematics achievement at tertiary level.
The participants of the experiment were all first-year mathematics students at [ ] University, comprising 114 persons in total, attending the Algebra and Number Theory course. During the analysis, we discounted the data relating to students who had previously taken the course, leaving 72 persons in all, 26 male and 46 female. Their ages were between 18 and 23.
The regular course materials for the Algebra and Number Theory lectures and problem-solving seminars were used based on the textbook by Niven et al. (1991): An Introduction to the Theory of Numbers, 5th ed.
The course, which the students attended in six groups, consisted of one 60-minute lecture and one 90-minute problem-solving seminar per week for a total of 13 weeks. Each student completed a competence-level test at the initial class. Three of the six groups were randomly selected as the experimental group, the other three were the control group; 37 students were in the experimental group, and 35 were in the control group. The teachers of the control groups and the experimental groups were in pairs. Pairs were created according to teaching experience, with 1-1 experienced teacher, 1-1 demonstrator, and 1-1 doctoral student in the control and experimental groups.
The problem-solving seminars consisted of tasks based on the theoretical subject matter of the previous week’s lecture, which were solved collectively with the help of a professor. The structure of each lesson for the control group was the following: at the beginning of the class, they wrote a short test on the previous week’s material (as it is traditional in the case of this subject). This was followed by the discussion of homework and the main part, which is problem-solving with the aid of the professors. In the experimental group, the structure was almost identical, the only difference was that there was no test at the beginning of the lesson, instead, they had a test at the end of the class. Our method resembled to that of Lyle and Crawford (2011) in that students had to complete tasks similar to those encountered during the class (see Appendix A). The end-of-class test consisted of 2 problems and members of the experimental group had to solve it individually, without any help (while members of the control group solved it with the professors, as with all other problems). The solutions of the problems of the end-of-class test were not discussed in the experimental groups, only if the students asked for it. By solving a problem students could gain 1-1 points. In case their solution was perfect, they got 1 point. If they made a little mistake, they could still get 0,5 points. Otherwise, they got 0 points. When revising the papers, we tried to be objective. The teachers of the course had a short conversation every week when they discussed how to correct the tests. After these conversations, students' tests were corrected by their teacher. Finally, the lecturer reviewed the corrections of all the papers. All students (both in the control and experimental group) had to reach at least 50% of the aggregate score of the seminar tests. This was the prerequisite for the final examination.
In the last problem-solving seminar, both groups completed a final test consisting of five problems (see Appendix B), the score of which determined their final grades.
The evaluation of the final test was the following: the perfect solution for each problem was awarded 6 points. Sub-scores for partial solutions, evaluation of the, most common errors and the general policies of correction were included in a detailed scoring guide, written by the lecturer. Students' tests were corrected by their teacher (with the help of the lecturer, if consultation was necessary), according to these guidelines. Finally, the lecturer reviewed the corrections of all the papers.
The following contains some analysis of the problems in the final test. The first problem is a typical example requiring procedural knowledge. Procedural (vs. conceptual) means that this kind of problem always can be solved using the same method. Plus, both the procedure and the calculations are rather easy. This problem can even be solved using only high school knowledge. However, the problem is still complex. Although the general method can be practiced to a great extent, you need a trick in each step, and this trick depends on the numbers appearing in the problem.
The second problem can also be solved procedurally, but it is one step more complicated. The knowledge required to solve this problem is brand new university knowledge; there is no way to solve it with high school techniques. The procedure, as in the previous case, is always the same, but an extra formula must be applied beforehand. (The formula is known by everybody.) As in the first problem, with a lot of practice, students can be prepared for the midterm, but for long-term application, conceptual knowledge is also required in this case. As well as in the previous case, you can acquire the general method, but you still need a trick, which depends on the actual numbers of the problem. This adds a lot to the complexity of the problem. This calculation cannot be reversed even by the most modern, fastest computers. For example, bank cryptography is based on this method: our computer generates a code using this method and this way the code cannot be broken.
The third problem requires all possible abstract skills gained during study. The concept it uses is rather difficult and is strongly connected to the notion of multiplicative order from abstract algebra, which is by far the hardest concept in the material. The knowledge of this concept can be checked in several different ways, and each way is challenging. This was the last topic taught before the midterm; hence, there was a chance that students did not have enough time to conceptualize the notion. Additionally, we must mention that this concept was not practiced during the problem-solving seminars, only during the lecture.
The fourth problem is the most complex. The solution requires the application of several different strategies such that each must be selected from some lists of different strategies, each of which contains infinite strategies. Although the material taught and the form of the problem suggested the lists of strategies, it is not obvious which of the lists has to be applied. If one of the strategies was wrongly selected, participants had to start solving the problem from the beginning. The solution of this problem definitely requires a conceptual understanding of most topics. Furthermore, this function has several ways of formulation and no matter which one we choose we must work out how it can be interpreted in order to use it for the actual problem. When we have the interpretation, it is still complex how to use it because the formula consists of several components.
Problem 5 is always the most difficult problem with a solution that is easy to understand and very hard to find. For the solution, you need to see the global structure of the material and make deductions on the features of the items based on the structure. Then you need to decide on which items the deduction is true and then step back to the structure to find whether there exists such item or not.
When analysing the results, we found that there is no difference among genders (F(1,67) = 0.29 p > 0.05 ηp2 =0.004 ), as well as no significant interaction (F(1,67) = 3.92 p > 0.05 ηp2 =0.055, ), so we can state that gender has no effect at all. Thus, in the following, we do not include this aspect in the analysis.
The score of the competence-level test was M = 57.24; SD = 19.50 in the experimental group and M = 60.46; SD = 20.12 in the control group. The score of the final exams was M = 17.22; SD = 5.74 in the experimental group and M = 14.29; SD = 5.91 in the control group, where the maximum score was 30.
We wanted to eliminate the effect of differences in prior knowledge on the scores of the final test, so we analysed the data using ANCOVA (Cohen, 1988, pp. 287-288). When comparing the experimental and control groups based on the final exam scores and controlling for their competence-level test scores, we found that the experimental group performed significantly better than the control group, F(1,69) = 9.19 p<0.001, ηp2 = 0.118, despite the fact that their performance on the competence exams was significantly worse, F(1, 69) = 32.79 p < 0.001 η p2 = 0.322
To examine the effect of differences in individual competence, we divided the students in both the experimental and control groups into below-average, average, and above-average groups based on their competence-level tests, placing those with ±½ SD around the mean into the “average” category, those with under ½ SD of the mean into the “below average” category, and those with over ½ SD of the mean placed into the “above average” category. The average scores of their final exams are shown in Figure I. below.
FIGURE I. The performance of below-average, average, and above-average students within the experimental and control groups. Error bars represent ±1 SE.

Source: Compiled by author
The data were analysed using a 2 × 3 (experimental-control, below average-average-above average) ANCOVA. The experimental group performed significantly better than the control group F(1,66 ) = 7.52 p < 0.001, ηp2 = 0.102; the difference of the groups based on competence is significant, F(2,66) = 13.02 p < 0.001, ηp2 = 0.283; based on the Sidak correction for multiple comparisons, the performance of all three groups differed significantly from each other, and there was no significant interaction, F(2 ,66) = 0.86 p>0.05, ηp2 = 0.026; the testing effect was shown to be independent of individual competence.
The purpose of this study was partly to examine if the advantages of test-enhanced learning over traditional learning techniques — problem-solving exercises — may be observed using the complex mathematical curriculum of an actual educational environment. This was important because the testing effect has not yet been demonstrated in relation to higher-level mathematics and an actual educational environment. Furthermore, test-enhanced learning was shown to lose its advantage when its object concerns deductive tasks and complex materials (Tran et al., 2015) or may result in weaker performance (Leahy et al., 2015). In contrast, our own results indicate that test-enhanced learning has a significant advantage in relation to solving complex mathematical problems. The learning process of the experimental group and the control group was tightly synchronised so that they get familiar with the same concepts, the same problems, and exactly the same tasks. The experimental group’s performance showed significant improvement despite that this group had less mathematical understanding at the beginning of the semester. They reached better results in the final examination than the control group studying with traditional methods.
The other aim of our study was to investigate Khanna’s (2015) idea: whether graded tasks in fact result in weaker performance. In their experiment, they were unable to demonstrate the benefits of test-enhanced learning over traditional revision practices. They posited that the negative results were due to anxiety caused by testing, which impedes performance. - students of their courses completed a 6-item questionnaire on their feelings about the inclusion of quizzes in the course. Other previous studies show the effectiveness of test-enhanced learning when the final test occurs under stress (such as in an exam) (Szőllősi et al., 2017). Multiple measures of stress levels were applied, such as anxiety tests like STAI and PANAM, and saliva sampling for measuring the cortisol level. The results favoured the ecological validity of retrieval-based learning. As we already mentioned in the introduction, anxiety backed up by higher intrinsic motivation may, in fact, serve to improve performance (Wang et al., 2015). Our results strengthen the positivity of the testing effect, in the sense that graded quizzes produced significantly better performance. We also examined the role of differences in individual competence as the existing literature on the subject was contradictory. In Carpenter et al. (2016), the testing effect was only observed in above-average students while Orr and Foster (2017) identified it in below-average, average, and above-average individuals alike. In our opinion, the two experiments differ because, while Carpenter et al. (2016) grouped the participants according to competence only after the completion of the course based on their performance, Orr and Foster (2017) compared them based on the results of the first three tests. In our own study, we administered a preliminary test prior to the onset of the classes to gauge competence and thereby determine the below-average, average, or above-average status of participants. Our results show, similarly to those of Orr and Foster (2017), that the testing effect appears independently of individual mathematical competence.
One limitation within our study is that it does not uncover what other possible individual competencies may influence the effect of test-enhanced learning past one’s mathematical competence—for example, Gf-I—as this question was not examined. Another limitation is that we did not monitor changes in test anxiety within the experimental and control groups, which might have been relevant in finding out whether decreased anxiety among the control group taking weekly tests could have been the (or a) cause for their better performance during the final examination. In order to reduce the teachers’ effect, we chose “teacher-pairs” for the experiment, according to their teaching experience.
The question of finding the best way to test students with different mathematical abilities is an open and interesting one. We suspect that mathematical ability and how the test is designed (difficulty and form of questions) are somehow related to the rate of students’ progress. In our experiments, we found that the kind of retrieval practice we applied can be an effective way of learning higher mathematics that professors can implement in their lessons to enhance students’ performances and is beneficial for students with either low, average, or high mathematical competence.
Agarwal, P. K., Bain, P. M., y Chamberlain, R. W. (2012). The value of applied research: retrieval practice improves classroom learning and recommendations from a teacher, a principal, and a scientist. Educational Psychology Review, 24(3), 437–448. https://doi.org/10.1007/s10648-012-9210-2
Avvisati, F., & Borgonovi, F. (2020). Learning mathematics problem solving through test practice: A randomized field experiment on a global scale. Educational Psychology Review, 32(3), 791–814. https://doi.org/10.1007/s10648-020-09520-6
Balota, D. A., Duchek, J. M., Sergent-Marshall, S. D., & Roediger, H.L. (2006). Does expanded retrieval produce benefits over equal-interval spacing? Explorations of spacing effects in healthy aging and early stage Alzheimer’s disease. Psychol. Aging, 21(1), 19–31. https://doi.org/10.1037/0882-7974.21.1.19
Brewer, G. A., & Unsworth, N. (2012). Individual differences in the effects of retrieval from long-term memory. Journal of Memory and Language, 66, 407–415. https://doi.org/10.1016/j.jml.2011.12.009
Butler, A. C. (2010). Repeated testing produces superior transfer of learning relative to repeated studying. Journal of experimental psychology. Learning, memory, and cognition, 36(5), 1118–1133. https://doi.org/10.1037/a0019902
Carpenter, S. K., Lund, T. J. S., Coffman, C. R., Armstrong, P. I., Lamm, M. H., & Reason, R. D. (2016). A classroom study on the relationship between student achievement and retrieval-enhanced learning. Educational Psychology Review, 28(2), 353–375. https://doi.org/10.1037/xap0000145
Cohen, J. (1988). Statistical power analysis for the behavioral sciences. Second Edition. Hillsdale, NJ: Lawrence Erlbaum Associates, Publishers.
Donoghue, G. M., & Hattie, J. A. C. (2021). A meta-analysis of ten learning techniques. Frontiers in Education, 6:581216. https://doi.org/10.3389/feduc.2021.581216
Dunlosky, J., Rawson, K. A., Marsh, E. J., Nathan, M. J., & Willingham, D.T. (2013). Improving students’ learning with effective learning techniques: Promising directions from cognitive and educational psychology. Psychological Science in the Public Interest, 14(1) 4–58. https://doi.org/10.1177/1529100612453266
Eglington, L. G., & Kang, S.H.K. (2018). Retrieval practice benefits deductive inference. Educational Psychology Review, 30(1), 215–228. https://doi.org/10.1007/s10648-016-9386-y
Emmerdinger, K. J., & Kuhbandner, CH. (2019). Tests improve memory – no matter if you feel good or bad while taking them. Memory, (27)8, 1043–1053. https://doi.org/10.1080/09658211.2019.1618339
Fazio, L. K (2019). Retrieval practice opportunities in middle school mathematics teachers’ oral questions. British Journal of Educational Psychology, 89(2), 653–669. https://doi.org/10.1111/bjep.12250
Hostetter, A. B., Penix, E. A., Norman, M. Z., Batsell, W. R., & Carr, Th, H. (2019). The role of retrieval practice in memory and analogical problem-solving. Quarterly Journal of Experimental Psychology 72(4), 858–871. https://doi.org/10.1177/1747021818771928
Kang, S. H. K., McDermott, K. B., & Roediger, H. L. III. (2007). Test format and corrective feedback modify the effect of testing on long-term retention. European Journal of Cognitive Psychology, 19(4-5), 528–558. https://doi.org/10.1080/09541440601056620
Karpicke, J. D. (2017). Retrieval-based learning: A decade of progress. In: Byrne, J. H. (Ed.). Learning and Memory: A comprehensive reference. (2nd ed., Vol. 2) (pp. 487–514). https://doi.org/10.1016/B978-0-12-809324-5.21055-9
Karpicke, J. D., & Aue, W., R. (2015). The testing effect is alive and well with complex materials. Educational Psychology Review, 27, 317–326. https://doi.org/10.1007/s10648-015-9309-3
Karpicke, J. D., & Blunt, J. R. (2011). Retrieval practice produces more learning than elaborative studying with concept mapping. Science, 331, 772–775. https://doi.org/10.1126/science.1199327
Khanna, M. M. (2015). Ungraded pop quizzes: Test-enhanced learning without all the anxiety. Teaching of Psychology, 42, 174–178. https://doi.org/10.1177/0098628315573144
Larsen, D.P., Butler, A.C., & Roediger, H.L. 3rd. Comparative effects of test-enhanced learning and self-explanation on long-term retention. Med Educ., 2013 Jul; 47(7), 674–82. https://doi.org/10.1111/medu.12141
Leahy, W., Hanham, J., & Sweller, J. (2015). High element interactivity information during problem solving may lead to failure to obtain the testing effect. Educational Psychology Review, 27, 265–289. https://doi.org/10.3389/fpsyg.2018.01483
Lyle, K. B., Bego, C. R., Hopkins, R. F., Hieb, J. L., & Raltson, P. A. (2020). How the amount and spacing of retrieval practice affect the short- and long-term retention of mathematics knowledge. Educational Psychology Review, 32, 277–295. https://doi.org/10.1007/s10648-019-09489-x
Lyle, K. B., & Crawford, N. A. (2011). Retrieving essential material at the end of lectures improves performance on statistics exams. Teaching of Psychology, 38(2), 94–97. https://doi.org/10.1177/0098628311401587
Lyle, K. B., Hopkins, R. F., Hieb, J. L., & Ralston, P. A. (2016). Spaced retrieval practice increases college students’ short- and long-term retention of mathematics knowledge. Educational Psychology Review, 28(4), 853–873. https://doi.org/10.1007/s10648-015-9349-8
Niven, I., Zuckerman, H. S., & Montgomery, H. L. (1991). An Introduction to the Theory of Numbers (5th ed.) New York: John Wiley and Sons. Inc.
Orr, R., & Foster, S. (2017). Increasing student success using online quizzing in introductory (majors) biology. CBE Life Sciences Education, 12(3), 509–514. https://doi.org/10.1187/cbe.12-10-0183
Peterson, D., & Wissman, K. (2018). The testing effect and analogical problem-solving. Memory, 26(10) 1–7. https://doi.org/10.1080/09658211.2018.1491603
Roediger H. L., & Butler, A. C., (2011). The critical role of retrieval practice in long-term retention. Trends in Cognitive Sciences, 15(1) 20–27. https://doi.org/10.1016/j.tics.2010.09.003
Rowland, C. A. (2014). The Effect of Testing Versus Restudy on Retention: A Meta-Analytic Review of the Testing Effect. Psychological Bulletin, 140(6), 1432–1463. https://doi.org/10.1037/a0037559
Smith, M. A., & Karpicke, J. D. (2014). Retrieval practice with short-answer, multiple-choice, and hybrid tests. Memory, 22(7), 784–802. https://doi.org/10.1080/09658211.2013.831454
Szőllősi, Á., Keresztes, A., Novák, B., Szászi, B., & Racsmány, M. (2017). The Testing Effect is Preserved in Stressful Final Testing Environment. Applied Cognitive Psychology. 31. https://doi.org/10.1002/acp.3363
Tran, R., Rohrer, D., & Pashler, H. (2015). Retrieval practice: The lack of transfer to deductive inferences. Psychonomic Bulletin &Review, 22(1), 135–140. https://doi.org/10.3758/s13423-014-0646-x
Tse, C.-S., & Pu, X., (2012). The effectiveness of test-enhanced learning depends on trait test anxiety and working-memory capacity. J. Exp. Psychol. Appl. 18 (3), 253–264. https://doi.org/10.1037/a0029190
van Eersel, G. G, Verkoeijen, P. P. J. L., Povilenaite, M., & Rikers, R. (2016). The testing effect and far transfer: The role of exposure to key information. Frontiers in Psychology, 7, Article 1977. https://doi.org/10.3389/fpsyg.2016.01977
van Gog, T., & Sweller, J. (2015). Not new, but nearly forgotten: The testing effect decreases or even disappears as the complexity of learning materials increases. Educational Psychology Review, 27(2), 247–264. https://doi.org/10.1007/s10648-015-9310-x
Wang, Z., Lukowski, S. L, Hart, S. A., Lyons, I. M., Thompson, L. A., Kovas, Y., & Petrill, S. A. (2015). Is math anxiety always bad for math learning? The role of math motivation. Psychological Science, 26(12), 1863–1876. https://doi.org/10.1177/0956797615602471
Wong, S., S., H., Ng, G., J., P., Tempel, T.& Lim, S., W., H. (2019). Retrieval Practice Enhances Analogical Problem Solving. The Journal of Experimental Education, 87(1) 128–138. https://doi.org/10.1080/00220973.2017.1409185
Yeo, D. J., & Fazio, L. K. (2019). The optimal learning strategy depends on learning goals and processes : retrieval practice versus worked examples. Journal of Educational Psychology, 111(1), 73–90. https://doi.org/10.1037/edu0000268
Contact Address: Csilla Zámbó. Eötvös Loránd University, Faculty of Primary and Pre-School Education, Department of Mathematics. 1126 Budapest, Kiss János altb. u. 40. E-mail: zambo.csilla@tok.elte.hu
1) Determine all positive solutions of the following system of congruences below.
4) Prove that the equation
has no solutions among the integers.
2) Find the remainder of 73737311 99993330002 modulo 73.
OR
Find the remainder of modulo 43.
5) For which positive integers n is
3) We know that 11 is a primitive root modulo 29. Is it true that 115 and 117are primitive roots?