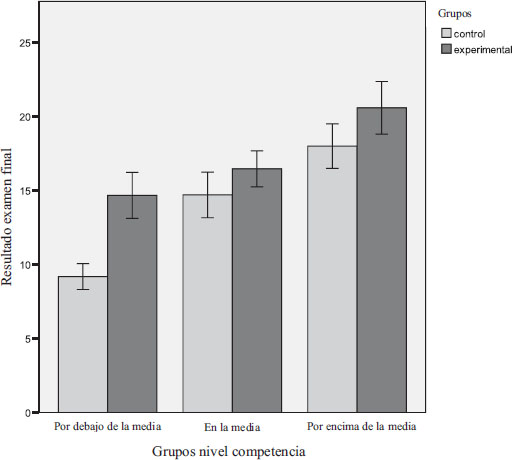
FIGURA I. El rendimiento de los alumnos por debajo de la media, en la media y por encima de la media en los grupos experimental y de control. Las barras de error representan ±1 SE.
Fuente: Elaboración propia
https://doi.org/10.4438/1988-592X-RE-2023-401-584
Csaba Szabó
https://orcid.org/0000-0003-4783-5411
Eötvös Loránd University, Faculty of Science
MTA-ELTE Theory of Learning Mathematics Research Group
Csilla Zámbó
https://orcid.org/0000-0002-7230-7023
Eötvös Loránd University, Faculty of Primary and Pre-School Education
MTA-ELTE Theory of Learning Mathematics Research Group
Anna Muzsnay
https://orcid.org/0000-0003-4045-0527
University of Debrecen
MTA-ELTE Theory of Learning Mathematics Research Group
Janka Szeibert
https://orcid.org/0000-0002-4267-9360
Eötvös Loránd University, Faculty of Primary and Pre-School Education
MTA-ELTE Theory of Learning Mathematics Research Group
László Bernáth
https://orcid.org/0000-0002-8314-6560
Eötvös Loránd University, Faculty of Education and Psychology
MTA-ELTE Theory of Learning Mathematics Research Group
Resumen
Recuperar información de la memoria puede reforzar el recuerdo de la propia información recuperada. El uso estratégico de la recuperación para mejorar la memoria y ayudar a la retención a largo plazo se conoce como aprendizaje potenciado por test o aprendizaje potenciado por recuperación. El aprendizaje potenciado por test ha demostrado su eficacia en relación con diferentes materiales de aprendizaje, pero estos experimentos se realizaron principalmente en entornos de laboratorio y se centraron sobre todo en la memorización. Nuestro objetivo era explorar la eficacia del aprendizaje potenciado por test utilizado para la enseñanza de matemáticas de nivel universitario. El experimento se llevó a cabo en entornos de aula, en relación con asignaturas obligatorias. Los participantes fueron seis grupos de profesores de matemáticas en formación. Tres grupos aprendieron Teoría de los Números utilizando el efecto test, y los otros tres aprendieron utilizando métodos tradicionales. Los grupos experimental y control aprendieron exactamente la misma información en la clase y realizaron el mismo examen final. El grupo experimental obtuvo un rendimiento significativamente mejor que el grupo control, a pesar de que su rendimiento en los exámenes de competencia inicial fue significativamente peor. Los resultados indican que el aprendizaje potenciado por test tiene una ventaja significativa en la resolución de problemas matemáticos complejos. Para examinar el efecto de las diferencias en la competencia individual, dividimos a los estudiantes de ambos grupos experimental y control a su vez en grupos de rendimiento bajo, medio y alto. La eficacia del aprendizaje potenciado por test se demostró en los tres niveles de rendimiento. En cuanto a los tres pares de grupos, los miembros del grupo experimental que utilizó el aprendizaje potenciado por test obtuvieron mejores resultados que los del grupo control.
Palabras clave: efecto test, práctica de recuperación, matemáticas, problemas complejos, diferencias individuales.
Abstract
Retrieving information from memory can strengthen one’s memory of the retrieved information itself. The strategic use of retrieval to enhance memory and help long-term retention is known as test-enhanced learning or retrieval practice. Test-enhanced learning has been proven effective concerning different learning materials, but these experiments were primarily conducted in laboratory environments and focused mainly on memorization. Our aim was to explore the efficacy of test-enhanced learning used for teaching mathematics at university level. The experiment was carried out in classroom settings, concerning obligatory courses. The participants were six groups of undergraduate pre-service mathematics teachers. Three groups learned Number Theory using the testing effect, and the other three learned using traditional methods. The experimental and control groups learned the exact same information in the lecture and wrote the same final test. The experimental group performed significantly better than the control group, although their performance on the initial competence exams was significantly worse. The results indicate that test-enhanced learning has a significant advantage in solving complex mathematical problems. To examine the effect of differences in individual competence, we divided the students in both experimental and control groups into low-, middle-, and high-performing groups. The efficacy of test-enhanced learning was demonstrated in all the three performance levels. Regarding the three pairs of groups, members of the experimental group using test-enhanced learning performed better than those of the control group.
Keywords: testing effect, retrieval practice, mathematics, complex problems, individual differences.
Recuperar información de la memoria tras una fase inicial de aprendizaje mejora la retención a largo plazo más que volver a estudiar el material, una ventaja denominada efecto test (Roediger y Butler, 2011; Rowland, 2014). El efecto test se ha demostrado con diversos tests de práctica, materias y grupos de edad (Karpicke, 2017), incluida la educación terciaria (Butler, 2010). Sin embargo, estos experimentos se realizaron en su mayoría en entornos de laboratorio relativos a la memorización de textos o palabras. Solo ha habido un número limitado de experimentos en el campo de las matemáticas, en entornos educativos reales (Lyle y Crawford, 2011; Lyle, Hopkins et al., 2016; Fazio 2019; Lyle, Bego et al., 2020).
Las pruebas aumentan la eficacia, no solo de la retención palabra-por-palabra – en oposición a la relectura – sino también de la aplicación de los conocimientos recién adquiridos. Smith and Karpicke (2014) han demostrado que los grupos que estudian con tests obtuvieron mejores resultados que el grupo control, no solo en tareas de retención palabra por palabra, sino también en tareas que exigen síntesis de la información dentro del texto dado. Además, se demostró que los conocimientos adquiridos con la práctica de recuperación no solo eran más aplicables dentro la materia del texto dado que los conocimientos basados en la relectura, sino que también eran más fácilmente transferibles a otras áreas (Butler, 2010; van Eersel et al., 2016).
La sólida evidencia de un efecto directo de las pruebas o test sugiere que la práctica de la recuperación puede considerarse una de las técnicas de aprendizaje más eficaces. (Karpicke y Blunt, 2011; Larsen et al., 2013; Dunlosky et al., 2013; Donoghue y Hattie, 2021). Sin embargo, existen ciertos ámbitos en los que la demostración del efecto test ha fracasado, o a producido resultados contradictorios.
Un impedimento potencial se refiere a los resultados de Khanna (2015) basados en un estudio realizado dentro de un curso de introducción a la psicología. Los estudiantes fueron colocados en grupos de “examen no evaluado”, “examen evaluado” y “sin examen”, y a los dos primeros se les administraron seis exámenes sorpresa en el semestre. Los resultados muestran que el grupo “no evaluado” obtuvo mejores resultados que los otros dos grupos, y no hubo diferencias de rendimiento entre los grupos “evaluado” y “sin examen”. La explicación de Khanna para este resultado es que los niveles más altos de ansiedad pueden eliminar el efecto test en el grupo “evaluado”. Sin embargo, estas conclusiones contradicen los hallazgos de Agarwal et al., (2012) de que la disminuye en los alumnos que estudian con tests frecuentes, y los resultados de Tse y Pu (2012) que demostraron la eficacia del efecto test en el caso tanto de personas con poca como con mucha ansiedad. Una posible solución a esta contradicción es que la ansiedad solo perjudica el rendimiento en el estudio en el caso de una motivación intrínseca débil, y si está respaldada por una motivación intrínseca más fuerte, la ansiedad puede, de hecho, servir para mejorar el rendimiento (Wang et al., 2015). Los resultados de Emmerdinger y Kuhbandner (2019) pueden aportar otra solución a la contradicción. Ellos encontraron que el efecto test aparece independientemente del estado emocional (negativo, neutral o positivo) de los participantes.
En cuanto a la forma del test, tanto las pruebas de respuesta corta como las de elección múltiple son formas más eficaces de aprendizaje que la relectura (Kang et al, McDermott, and Roediger, 2007). La eficacia de las pruebas puede variar en función de la presencia de retroalimentación. Si se incluye retroalimentación, las preguntas de respuesta corta son más beneficiosas; de lo contrario, las pruebas de opción múltiple son más efectivas.
Otra contradicción se refiere al papel de las diferencias individuales en el aprendizaje potenciado por test. Orr y Foster (2017) realizaron su análisis dentro un curso de biología en la que los estudiantes tenían la opción de participar en pruebas administradas periódicamente a lo largo del mismo. Los que participaron sistemáticamente en los tests obtuvieron mejores resultados en el examen final que los que no lo hicieron. Además, lo más importante desde nuestro punto de vista es que esta ventaja se observó tanto en estudiantes con aptitudes superiores a la media, como en la media e inferiores a la media. Por el contrario, los resultados de Carpenter et al. (2016), también dentro de un curso de biología, muestran que el aprendizaje potenciado por test solo fue eficaz en estudiantes con habilidades superiores a la media y que no se observó ninguna mejora en estudiantes con habilidades medias e inferiores a la media. Esto dificulta enormemente la aplicación del aprendizaje potenciado por test en el aula. Sin embargo, los resultados de Carpenter et al. (2016) contradicen la afirmación de Brewer y Unsworth (2012) de que las personas con menor inteligencia general fluida (I-Gf) se beneficiaron más del estudio basado en test que las personas con mayor I-Gf que el aprendizaje potenciado por test podría no observarse en todos los individuos de mayor nivel Gf-I. Además, Balota et al. (2006) demostraron los beneficios del efecto de los tests entre las personas con demencia de tipo Alzheimer. Este resultado sugiere que las pruebas son beneficiosas para las personas con capacidades medias o inferiores a la media, e incluso para las personas con problemas de memoria.
El tercer factor que ha producido resultados contradictorios se refiere al papel del nivel de complejidad del objeto de estudio. Van Gog y Sweller (2015) sostienen que el efecto test solo puede observarse cuando no hay interacción entre los ítems a aprender, por ejemplo, cuando se aprende el vocabulario de una lengua extranjera; en materias más complejas, disminuye o desaparece por completo. (Sin embargo, véase Karpicke y Aue (2015) para contraargumentos teóricos). Leahy et al. (2015) observaron el efecto test relacionado con materias de estudio complejas en pruebas de retención inmediata, y no detectaron ningún efecto pasada una semana. Tran et al. (2015) llegaron a un resultado negativo similar, cuyos grupos de “revisión” y “prueba” tuvieron que aprender consecutivamente frases que aparecían describiendo varios escenarios. En la prueba final, aunque la retención de las frases individuales mostró el efecto test, no hubo diferencias en el rendimiento entre los dos grupos en cuanto a la obtención de conclusiones basadas en el contenido de las frases. En otras palabras, descubrieron que, en tareas complejas que requieren un pensamiento deductivo, el efecto test desaparece. Eglington y Kang (2018) repitieron el experimento de Tran et al. (2015) con una modificación (las frases se mostraban en el monitor todas a la vez, no de una en una); sus resultados demostraron los beneficios del efecto test en esta tarea deductiva.
En el estudio de Peterson y Wissmann (2018), el efecto de recuperación no tuvo ninguna ventaja en comparación con el reestudio en el caso de la resolución de problemas complejos que requerían pensamiento analógico. A pesar de estos resultados, Wong et al. (2019) y Hostetter et al. (2019) demostraron los beneficios del aprendizaje por recuperación en la resolución de problemas analógicos. Lo más probable es que, en el caso de Peterson y Wissmann (2018), la ineficacia del efecto de recuperación pueda explicarse no (o no solo) por el requisito de pensamiento analógico, sino quizá (también) por la complejidad de los problemas o algunos otros elementos del diseño experimental. Según los resultados mencionados, en las tareas que exigen un pensamiento complejo o deductivo, no está clara la ventaja del aprendizaje potenciado por test sobre el aprendizaje por relectura. Además, como han demostrado los resultados de Carpenter et al. (2016) y Brewer y Unsworth (2012), los papeles de las diferencias de competencia individual también son ambiguos.
Los problemas matemáticos exigen habilidades deductivas y de resolución de problemas desarrolladas, y los propios problemas son bastante complejos. Desarrollar habilidades de resolución de problemas en matemáticas requiere la aplicación de procedimientos y una comprensión conceptual profunda, no solo memorización. Aunque solo ha habido unas pocas investigaciones sobre el efecto test en la resolución de problemas matemáticos en un entorno escolar real, estudios recientes sugieren que el uso intensivo de la práctica de recuperación puede ser una forma eficaz de aprender (Lyle y Crawford, 2011; Fazio 2019; Lyle et al. 2016; Lyle et al. 2020). El trabajo de Avvisati y Borgonovi (2020) se refiere a la resolución de problemas en matemáticas. Aunque no se trata de un entorno educativo real en el sentido de que midieron el efecto de un único test de práctica, su investigación con una muestra amplia es relevante para nosotros, ya que utiliza material educativo. Demuestran que el número de problemas matemáticos en el primer examen tuvo un efecto positivo pequeño en el rendimiento medio en matemáticas en el segundo test. En el experimento de Yeo y Fazio (2019), se examinó la eficacia de la práctica de recuperación y los ejemplos trabajados para diferentes objetivos de aprendizaje. La estrategia de aprendizaje óptima dependía del intervalo de retención y de la naturaleza de las materias. Cuando el objetivo de los estudiantes era recordar el texto de un ejemplo trabajado, pasada una semana, la prueba repetida fue más eficaz que el estudio repetido. Por otro lado, descubrieron que al aprender un procedimiento matemático novedoso y medir el rendimiento inmediatamente, el estudio repetido era más óptimo que la prueba repetida, independientemente de la naturaleza de la materia. Por último, el estudio de Lyle et al. (2011) es el más relevante para nuestra investigación. Incorporaron la práctica de recuperación en un curso de estadística para psicología añadiendo un breve ejercicio de recuperación de algún material esencial al final de cada clase. Este método aumentó significativa y sustancialmente las calificaciones de los exámenes. A los estudiantes les gusto la práctica de recuperación y la consideraron útil. En estudios posteriores de Lyle, se investigó la práctica de recuperación espaciada en el curso de pre cálculo. Sus resultados no han animado a explorar otros aspectos del efecto test en clases de matemáticas universitarias (Lyle et al. 2016, 2020).
Al aplicar la práctica de recuperación en un entorno escolar real, surgen dos cuestiones importantes: la forma de realizar las pruebas y las diferencias en las competencias matemáticas individuales. En cuanto a la forma de las pruebas, tanto las de respuesta corta como las de elección múltiple son formas más eficaces de aprender que la relectura (Kang et al. 2007). La eficacia de las pruebas puede variar en función de la presencia de retroalimentación en relación con el test de práctica. Si se incluye retroalimentación, las preguntas de respuesta corta son más beneficiosas; de lo contrario, las pruebas de opción múltiple son más eficaces (Kang et al., 2007). Asimismo, la cuestión de las diferencias en las competencias matemáticas individuales puede ser una cuestión central. Trataremos este aspecto con más detalle en el próximo capítulo, ya que su investigación formaba parte del objetivo de nuestro estudio.
En este estudio nos propusimos aplicar la práctica de recuperación en la enseñanza universitaria e investigar su eficacia en el aprendizaje de matemáticas superiores. A la hora de aplicar la práctica de recuperación en un entorno escolar real en matemáticas, no resulta evidente qué método utilizar ni cómo ponerlo en práctica. Debemos prestar atención al hecho de que la recuperación debe realizarse en un plazo de 24 horas, no debe haber copias ni trampas, no debe llevar mucho tiempo y los alumnos deben participar en ella. También hay que considerar la forma de la prueba y el tipo de preguntas.
Asimismo, nuestro objetivo es examinar si la eficacia de la práctica de recuperación depende de la competencia matemática individual. En el caso de la enseñanza de matemáticas universitarias, éste es un aspecto especialmente importante, ya que las diferencias entre los estudiantes que acceden a ella suelen ser enormes. Por esta razón, nuestro estudio examina un entorno educativo real y una materia regularmente solicitada. Compara el rendimiento de dos grupos de estudiantes en un curso de Álgebra y Teoría de Números que estudian con un método tradicional o con un método basado en test (recordando la materia de estudio en una ocasión, inmediatamente después de aprenderla) teniendo en cuenta los efectos de las diferencias en competencia individual. Para examinar las diferencias en competencia individual, agrupamos a los estudiantes basándonos no en su rendimiento global durante todo el curso, como hicieron Carpenter et al. (2016), sino en una prueba de nivel de competencia realizada en la clase inicial.
Los autores llevaron a cabo un estudio cuasi-experimental para averiguar si el efecto de recuperación conduce a una mejora en el rendimiento en matemáticas de nivel terciario.
Los participantes en el experimento fueron todos los estudiantes de primer curso de matemáticas de la Universidad de [], 114 personas en total, que asistían a la asignatura de Álgebra y Teoría de Números. Durante el análisis, se descontaron los datos relativos a los estudiantes que habían cursado la asignatura, quedando un total de 72 personas, 26 hombres y 46 mujeres. Sus edades estaban comprendidas entre los 18 y los 23 años.
Se utilizaron los materiales habituales de la asignatura para las clases de Álgebra y Teoría de Números y los seminarios de resolución de problemas, basados en el libro de texto de Niven et al. (1991): Introducción a la Teoría de los Números, 5ª ed. (1991).
El curso al que los alumnos asistieron en seis grupos, consistió en una lectura de 60 minutos y un seminario de resolución de problemas de 90 minutos por semana durante un total de 13 semanas. Cada alumno realizó una prueba de nivel de competencia en la clase inicial. Tres de los seis grupos se seleccionaron aleatoriamente como grupo experimental y los otros tres como grupos control; 37 estudiantes pertenecían al grupo experimental y 35 al grupo control. Los profesores de los grupos control y experimental formaban parejas. Las parejas se crearon según la experiencia docente, con 1-1 profesor experimentado, 1-1 docente y 1-1 estudiante de doctorado en los grupos control y experimental.
Los seminarios de resolución de problemas consistían en tareas basadas en la materia teórica de la clase de la semana anterior, que se resolvían colectivamente con la ayuda de un profesor. La estructura de cada lección para el grupo control era la siguiente: al principio de la clase, realizaban un breve test sobre el material de la semana anterior (como es habitual en el caso de esta asignatura). A continuación, se discutían los deberes y se pasaba a la parte principal, consistente en la resolución de problemas con ayuda de los profesores. En el grupo experimental, la estructura era casi idéntica, la única diferencia era que no había examen al principio de la clase, sino que se realizaba un examen al final de la clase. Nuestra prueba se parecía a la de Lyle y Crawford (2011) en que los estudiantes tenían que completar tareas similares a las discutidas durante la clase (ver Anexo A). El test de final de clase consistía en 2 problemas y los miembros del grupo experimental tenían que resolverlo individualmente, sin ayuda (mientras que los miembros del grupo de control lo resolvían con los profesores, al igual que el resto de problemas). Las soluciones de los problemas de la prueba al final de la clase no se discutían en los grupos experimentales, solo si los alumnos lo solicitaban. Al resolver un problema, los alumnos podían ganar 1-1 puntos. En caso de que su solución fuera perfecta, obtenían 1 punto. Si cometían un pequeño error, aún podían obtener 0,5 puntos. En caso contrario, obtenían 0 puntos. Al revisar los trabajos, intentábamos ser objetivos. Los profesores del curso mantenían una breve conversación cada semana en la que discutían cómo corregir los tests. Tras estas conversaciones, los tests de los alumnos eran corregidos por su profesor. Por último, el profesor revisaba las correcciones de todos los trabajos. Todos los alumnos (tanto del grupo control como del experimental) tenían que alcanzar al menos el 50% de la puntuación total de las pruebas del seminario. Esto era un requisito previo para el examen final.
En el último seminario de resolución de problemas, ambos grupos realizaron una prueba final, consistente en cinco problemas (véase el Anexo B), cuya puntuación determinó sus calificaciones finales.
La evaluación de la prueba final fue la siguiente: la solución perfecta de cada problema recibió 6 puntos. Las puntuaciones parciales, la evaluación de los errores más comunes y las normas generales de corrección se incluyeron en una guía de puntuación detallada, redactada por el profesor. Las pruebas de los alumnos eran corregidas por su profesor (con la ayuda del docente, si era necesario consultar), de acuerdo con estas directrices. Por último, el docente revisaba las correcciones de todos los trabajos. A continuación, se ofrece un análisis de los problemas de la prueba final.
El problema 1 es un ejemplo típico que requiere conocimientos procedimentales. Procedimental (frente a conceptual) significa que este tipo de problema siempre puede resolverse utilizando el mismo método. Además, tanto el procedimiento como los cálculos son bastante sencillos. Este problema puede resolverse incluso utilizando solo conocimientos de bachillerato. Sin embargo, el problema sigue siendo complejo. Aunque el método general se puede practicar en gran medida, se necesita un truco en cada paso, y este truco depende de los números que aparecen en el problema.
El problema 2 también puede resolverse procedimentalmente, pero es un paso más complicado. Los conocimientos necesarios para resolver este problema son conocimientos universitarios totalmente nuevos; no hay forma de resolverlo con técnicas de bachillerato. El procedimiento como en el caso anterior, es siempre el mismo, pero hay que aplicar previamente una formula extra. (La fórmula la conocen todos.) Como en el primer problema, con mucha práctica, los alumnos pueden estar preparados para el examen parcial, pero para la aplicación a largo plazo, en este caso también se requieren conocimientos conceptuales. Al igual que en el caso anterior, se puede adquirir el método general, pero sigue haciendo falta un truco, que depende de los números reales del problema. Esto añade mucha complejidad al problema. Este cálculo no puede ser invertido ni siquiera por los ordenadores más modernos y rápidos. Por ejemplo, la criptografía bancaria se basa en este método: nuestro ordenador genera un código utilizando este método y de esta manera el código no puede ser descifrado.
El problema 3 requiere todas las habilidades abstractas posibles adquiridas durante el estudio. El concepto que utiliza es bastante difícil y está fuertemente relacionado con la noción del orden multiplicativo del algebra abstracta, que es con diferencia el concepto más difícil de la materia. El conocimiento de este concepto puede comprobarse de varias formas distintas, y cada una de ellas supone un reto. Este fue el último tema que se enseñó antes del examen parcial; por lo tanto, existía la posibilidad de que los estudiantes no tuvieran tiempo suficiente para conceptualizar la idea. Además, debemos mencionar que este concepto no se practicó durante los seminarios de resolución de problemas, solo durante la clase.
El problema 4 es el más complejo. La solución requiere la aplicación de varias estrategias diferentes, cada una de las cuales debe seleccionarse de una lista de estrategias diferentes, cada una de las cuales contiene infinitas estrategias. Aunque el material enseñado y la forma del problema sugerían las listas de estrategias, no es obvio cuál de las listas debe aplicarse. Si se elegía mal una de las estrategias, los participantes tenían que empezar a resolver el problema desde el principio. La solución de este problema requiere sin duda una comprensión conceptual de la mayoría de los temas. Además, esta función tiene varias formas de formulación y elijamos la que elijamos, debemos averiguar cómo se puede interpretar para utilizarla en el problema real. Cuando tenemos la interpretación, sigue siendo complejo cómo utilizarla porque la fórmula consta de varios componentes.
El problema 5 es siempre el más difícil, con una solución fácil de entender y muy difícil de encontrar. Para la solución, hay que ver la estructura global de la materia y hacer deducciones sobre las características de los elementos basándose en la estructura. A continuación, hay que decidir en qué elementos la deducción es cierta y luego volver a la estructura para averiguar si existe tal elemento o no.
Al analizar los resultados, comprobamos que no hay diferencia entre géneros (F (1,67) = 0,29 p>0,05, ηp2 = 0,004), así como tampoco una interacción significativa (F(1,67) = 3,92 p>0,05, ηp2 = 0,055), por lo que podemos afirmar que el género no tiene ningún efecto. Por lo tanto, en adelante, no incluiremos este aspecto en el análisis.
La puntuación de la prueba de nivel de competencia fue M = 57,24; SD = 19,50 en el grupo experimental y M = 60,46; SD = 20,12 en el grupo control. La puntuación de los exámenes finales fue de M = 17,22; SD = 5,74 en el grupo experimental y M = 14,29; SD = 5,91 en el grupo control, siendo la puntuación máxima de 30.
Queríamos eliminar el efecto de las diferencias en los conocimientos previos sobre las puntuaciones del examen final, por lo que analizamos los datos mediante ANCOVA (Cohen, 1988). Al comparar los grupos experimental y de control basándonos en las puntuaciones del examen final y controlando sus puntuaciones en las pruebas de nivel de competencia, encontramos que el grupo experimental obtuvo resultados significativamente mejores que el grupo control, F(1,69) = 9,19 p<0,001, ηp2 = 0,118, a pesar de que su rendimiento en las pruebas de competencia fue significativamente peor, F(1,69) = 32,79 p<0,001, η p2 = 0,322.
Para examinar el efecto de las diferencias en la competencia individual, dividimos a los alumnos de los grupos experimental y de control en grupos por debajo de la media, medios y por encima de la media en función de sus exámenes de nivel de competencia, colocando a aquellos con ±½ SD alrededor de la media en la categoría “media”, a aquellos con menos de ½ SD de la media en la categoría “por debajo de la media”, y a aquellos con más ½ SD de la media colocados en la categoría “por encima de la media”. Las puntuaciones medias de sus exámenes finales se muestran en la Figura I. a continuación.
FIGURA I. El rendimiento de los alumnos por debajo de la media, en la media y por encima de la media en los grupos experimental y de control. Las barras de error representan ±1 SE.

Fuente: Elaboración propia
Los datos se analizaron utilizando un ANCOVA 2 × 3 (experimental-control, por debajo de la media-media-superior a la media). El grupo experimental obtuvo resultados significativamente mejores que el grupo control F(1,66 ) = 7,52 p<0,001, ηp2 = 0,102; la diferencia de los grupos basada en la competencia es significativa, F(2,66) = 13,02 p<0,001, ηp2 = 0,283; según la corrección de Sidak para comparaciones múltiples, el rendimiento de los tres grupos difiere significativamente entre sí, y no hay interacción significativa F(2,66) = 0,86 p>0,05, ηp2 = 0,026; se demostró que el efecto test es independiente de la competencia individual.
El propósito de este estudio era, en parte, examinar si las ventajas del aprendizaje potenciado por tests sobre las técnicas de aprendizaje tradicionales –ejercicios de resolución de problemas- pueden observarse utilizando el complejo currículo matemático de un entorno educativo real. Esto era importante porque el efecto test aún no se ha demostrado en relación con las matemáticas de nivel superior y un entorno educativo real. Además, se demostró que el aprendizaje potenciado por pruebas pierde su ventaja cuando su objeto se refiere a las tareas deductivas y materias complejas (Tran et al., 2015) o puede dar lugar a un rendimiento más débil (Leahy et al., 2015). Por el contrario, nuestros propios resultados indican que el aprendizaje potenciado por test tiene una ventaja significativa en relación con la resolución de problemas matemáticos complejos. El proceso de aprendizaje del grupo experimental y del grupo de control estuvo estrechamente sincronizado, de modo que se familiarizaron con los mismos conceptos, los mismos problemas y exactamente las mismas tareas. El rendimiento del grupo experimental mostró una mejora significativa a pesar de que este grupo tenía menos comprensión matemática al principio del semestre. Alcanzaron mejores resultados en el examen final que el grupo de control que estudiaba con métodos tradicionales.
El otro objetivo de nuestro estudio era investigar la idea de Khanna (2015): si las tareas calificadas dan lugar de hecho a un rendimiento más débil. En su experimento, no pudieron demostrar los beneficios del aprendizaje potenciado por test frente a las prácticas de repaso tradicionales. Postularon que los resultados negativos se debían a la ansiedad causada por los exámenes, que impide el rendimiento. – Los alumnos de sus cursos rellenaron un cuestionario de 6 preguntas sobre sus sentimientos acerca de la inclusión de cuestionarios en el curso. Otros estudios previos muestran la eficacia del aprendizaje potenciado por pruebas cuando la prueba final se produce bajo estrés (como en un examen) (Szőllősi et al., 2017). Se aplicaron múltiples medidas de los niveles de estrés, como pruebas de ansiedad como STAI y PANAM, y muestras de saliva para medir el nivel de cortisol. Los resultados favorecieron la validez ecológica del aprendizaje basado en la recuperación. Como ya mencionamos en la introducción, la ansiedad respaldada por una mayor motivación intrínseca puede, de hecho, servir para mejorar el rendimiento (Wang et al., 2015). Nuestros resultados refuerzan la positividad del efecto test, en el sentido de que cuestionarios calificados produjeron un rendimiento significativamente mejor. También examinamos el papel de las diferencias en la competencia individual, ya que la literatura existente sobre el tema era contradictoria. En Carpenter et al. (2016), el efecto test solo se observaba en estudiantes por encima de la media, mientras en Orr y Foster (2017) lo identificaron tanto en individuos por debajo de la media como en la media y por encima de la media. En nuestra opinión, los dos experimentos difieren porque, mientras que Carpenter et al. (2016) agruparon a los participantes según su competencia solo tras la finalización del curso en función de su rendimiento, Orr y Foster (2017) los compararon en función de los resultados de las tres primeras pruebas. En nuestro propio estudio, administramos una prueba preliminar antes del inicio de las clases para calibrar la competencia y determinar así la situación inferior a la media, media o superior a la media de los participantes. Nuestros resultados muestran, de forma similar a los de Orr y Foster (2017), que el efecto test aparece independientemente de la competencia matemática individual.
Una limitación de nuestro estudio es que no revela qué otras posibles competencias individuales pueden influir en el efecto del aprendizaje potenciado por tests sobre la competencia matemática de cada uno, por ejemplo -Gf-I-, ya que esta cuestión no se examinó. Otra limitación es que no controlamos los cambios en la ansiedad ante los exámenes dentro de los grupos experimental y de control, lo que podría haber sido relevante para averiguar si la disminución de la ansiedad entre el grupo de control que realizaba exámenes semanales podría haber sido la causa (o una de las causas) de su mejor rendimiento durante el examen final. Para reducir el efecto de los profesores, elegimos “parejas de profesores” para el experimento, en función de su experiencia docente.
La cuestión de encontrar la mejor manera de examinar a alumnos con distintas capacidades matemáticas es un tema abierto e interesante. Sospechamos que la capacidad matemática y la forma en que se diseña la prueba (dificultad y forma de las preguntas) están relacionadas de algún modo con el ritmo de progreso de los alumnos. En nuestros experimentos, comprobamos que el tipo de práctica de recuperación que aplicamos puede ser una forma eficaz de aprender matemáticas superiores que los profesores pueden poner en práctica en sus clases para mejorar el rendimiento de los alumnos y que resulta beneficiosa para estudiantes con una competencia matemática baja, media o alta.
Agarwal, P. K., Bain, P. M., & Chamberlain, R. W. (2012). The value of applied research: retrieval practice improves classroom learning and recommendations from a teacher, a principal, and a scientist. Educational Psychology Review, 24(3), 437–448. https://doi.org/10.1007/s10648-012-9210-2
Avvisati, F., & Borgonovi, F. (2020). Learning mathematics problem solving through test practice: A randomized field experiment on a global scale. Educational Psychology Review, 32(3), 791–814. https://doi.org/10.1007/s10648-020-09520-6
Balota, D. A., Duchek, J. M., Sergent-Marshall, S. D., & Roediger, H.L. (2006). Does expanded retrieval produce benefits over equal-interval spacing? Explorations of spacing effects in healthy aging and early stage Alzheimer’s disease. Psychol. Aging, 21(1), 19–31. https://doi.org/10.1037/0882-7974.21.1.19
Brewer, G. A., & Unsworth, N. (2012). Individual differences in the effects of retrieval from long-term memory. Journal of Memory and Language, 66, 407–415. https://doi.org/10.1016/j.jml.2011.12.009
Butler, A. C. (2010). Repeated testing produces superior transfer of learning relative to repeated studying. Journal of experimental psychology. Learning, memory, and cognition, 36(5), 1118–1133. https://doi.org/10.1037/a0019902
Carpenter, S. K., Lund, T. J. S., Coffman, C. R., Armstrong, P. I., Lamm, M. H., & Reason, R. D. (2016). A classroom study on the relationship between student achievement and retrieval-enhanced learning. Educational Psychology Review, 28(2), 353–375. https://doi.org/10.1037/xap0000145
Cohen, J. (1988). Statistical power analysis for the behavioral sciences. Second Edition. Hillsdale, NJ: Lawrence Erlbaum Associates, Publishers.
Donoghue, G. M., & Hattie, J. A. C. (2021). A meta-analysis of ten learning techniques. Frontiers in Education, 6:581216. https://doi.org/10.3389/feduc.2021.581216
Dunlosky, J., Rawson, K. A., Marsh, E. J., Nathan, M. J., & Willingham, D.T. (2013). Improving students’ learning with effective learning techniques: Promising directions from cognitive and educational psychology. Psychological Science in the Public Interest, 14(1) 4–58. https://doi.org/10.1177/1529100612453266
Eglington, L. G., & Kang, S.H.K. (2018). Retrieval practice benefits deductive inference. Educational Psychology Review, 30(1), 215–228. https://doi.org/10.1007/s10648-016-9386-y
Emmerdinger, K. J., & Kuhbandner, CH. (2019). Tests improve memory – no matter if you feel good or bad while taking them. Memory, (27)8, 1043–1053. https://doi.org/10.1080/09658211.2019.1618339
Fazio, L. K (2019). Retrieval practice opportunities in middle school mathematics teachers’ oral questions. British Journal of Educational Psychology, 89(2), 653–669. https://doi.org/10.1111/bjep.12250
Hostetter, A. B., Penix, E. A., Norman, M. Z., Batsell, W. R., & Carr, Th, H. (2019). The role of retrieval practice in memory and analogical problem-solving. Quarterly Journal of Experimental Psychology 72(4), 858–871. https://doi.org/10.1177/1747021818771928
Kang, S. H. K., McDermott, K. B., & Roediger, H. L. III. (2007). Test format and corrective feedback modify the effect of testing on long-term retention. European Journal of Cognitive Psychology, 19(4-5), 528–558. https://doi.org/10.1080/09541440601056620
Karpicke, J. D. (2017). Retrieval-based learning: A decade of progress. In: Byrne, J. H. (Ed.). Learning and Memory: A comprehensive reference. (2nd ed., Vol. 2) (pp. 487–514). https://doi.org/10.1016/B978-0-12-809324-5.21055-9
Karpicke, J. D., & Aue, W., R. (2015). The testing effect is alive and well with complex materials. Educational Psychology Review, 27, 317–326. https://doi.org/10.1007/s10648-015-9309-3
Karpicke, J. D., & Blunt, J. R. (2011). Retrieval practice produces more learning than elaborative studying with concept mapping. Science, 331, 772–775. https://doi.org/10.1126/science.1199327
Khanna, M. M. (2015). Ungraded pop quizzes: Test-enhanced learning without all the anxiety. Teaching of Psychology, 42, 174–178. https://doi.org/10.1177/0098628315573144
Larsen, D.P., Butler, A.C., & Roediger, H.L. 3rd. Comparative effects of test-enhanced learning and self-explanation on long-term retention. Med Educ., 2013 Jul; 47(7), 674–82. https://doi.org/10.1111/medu.12141
Leahy, W., Hanham, J., & Sweller, J. (2015). High element interactivity information during problem solving may lead to failure to obtain the testing effect. Educational Psychology Review, 27, 265–289. https://doi.org/10.3389/fpsyg.2018.01483
Lyle, K. B., Bego, C. R., Hopkins, R. F., Hieb, J. L., & Raltson, P. A. (2020). How the amount and spacing of retrieval practice affect the short- and long-term retention of mathematics knowledge. Educational Psychology Review, 32, 277–295. https://doi.org/10.1007/s10648-019-09489-x
Lyle, K. B., & Crawford, N. A. (2011). Retrieving essential material at the end of lectures improves performance on statistics exams. Teaching of Psychology, 38(2), 94–97. https://doi.org/10.1177/0098628311401587
Lyle, K. B., Hopkins, R. F., Hieb, J. L., & Ralston, P. A. (2016). Spaced retrieval practice increases college students’ short- and long-term retention of mathematics knowledge. Educational Psychology Review, 28(4), 853–873. https://doi.org/10.1007/s10648-015-9349-8
Niven, I., Zuckerman, H. S., & Montgomery, H. L. (1991). An Introduction to the Theory of Numbers (5th ed.) New York: John Wiley and Sons. Inc.
Orr, R., & Foster, S. (2017). Increasing student success using online quizzing in introductory (majors) biology. CBE Life Sciences Education, 12(3), 509–514. https://doi.org/10.1187/cbe.12-10-0183
Peterson, D., & Wissman, K. (2018). The testing effect and analogical problem-solving. Memory, 26(10) 1–7. https://doi.org/10.1080/09658211.2018.1491603
Roediger H. L., & Butler, A. C., (2011). The critical role of retrieval practice in long-term retention. Trends in Cognitive Sciences, 15(1) 20–27. https://doi.org/10.1016/j.tics.2010.09.003
Rowland, C. A. (2014). The Effect of Testing Versus Restudy on Retention: A Meta-Analytic Review of the Testing Effect. Psychological Bulletin, 140(6), 1432–1463. https://doi.org/10.1037/a0037559
Smith, M. A., & Karpicke, J. D. (2014). Retrieval practice with short-answer, multiple-choice, and hybrid tests. Memory, 22(7), 784–802. https://doi.org/10.1080/09658211.2013.831454
Szőllősi, Á., Keresztes, A., Novák, B., Szászi, B., & Racsmány, M. (2017). The Testing Effect is Preserved in Stressful Final Testing Environment. Applied Cognitive Psychology. 31. https://doi.org/10.1002/acp.3363
Tran, R., Rohrer, D., & Pashler, H. (2015). Retrieval practice: The lack of transfer to deductive inferences. Psychonomic Bulletin & Review, 22(1), 135–140. https://doi.org/10.3758/s13423-014-0646-x
Tse, C.-S., & Pu, X., (2012). The effectiveness of test-enhanced learning depends on trait test anxiety and working-memory capacity. J. Exp. Psychol. Appl. 18 (3), 253–264. https://doi.org/10.1037/a0029190
van Eersel, G. G, Verkoeijen, P. P. J. L., Povilenaite, M., & Rikers, R. (2016). The testing effect and far transfer: The role of exposure to key information. Frontiers in Psychology, 7, Article 1977. https://doi.org/10.3389/fpsyg.2016.01977
van Gog, T., & Sweller, J. (2015). Not new, but nearly forgotten: The testing effect decreases or even disappears as the complexity of learning materials increases. Educational Psychology Review, 27(2), 247–264. https://doi.org/10.1007/s10648-015-9310-x
Wang, Z., Lukowski, S. L, Hart, S. A., Lyons, I. M., Thompson, L. A., Kovas, Y., & Petrill, S. A. (2015). Is math anxiety always bad for math learning? The role of math motivation. Psychological Science, 26(12), 1863–1876. https://doi.org/10.1177/0956797615602471
Wong, S., S., H., Ng, G., J., P., Tempel, T. y Lim, S., W., H. (2019). Retrieval Practice Enhances Analogical Problem Solving. The Journal of Experimental Education, 87(1) 128–138. https://doi.org/10.1080/00220973.2017.1409185
Yeo, D. J., & Fazio, L. K. (2019). The optimal learning strategy depends on learning goals and processes : retrieval practice versus worked examples. Journal of Educational Psychology, 111(1), 73–90. https://doi.org/10.1037/edu0000268
Información de contacto: Csilla Zámbó. Eötvös Loránd University, Faculty of Primary and Pre-School Education, Department of Mathematics. 1126 Budapest, Kiss János altb. u. 40. E-mail: zambo.csilla@tok.elte.hu
1) Determina todas las soluciones positivas del siguiente sistema de congruencias de abajo.
4) Demuestra que la ecuación
no tiene soluciones entre los números enteros.
2) Encuentra el resto de 7373731199993330002 módulo 73.
O
Encuentra el resto de módulo 43.
5) Para qué números enteros positivos n es
3) Sabemos que 11 es una raíz primitiva módulo 29. ¿Es cierto que 115 y 117 son raíces primitivas?