La falta de influencia del tamaño de la clase sobre el rendimiento académico de los estudiantes: evidencia empírica para Andalucía1

The lack of influence of class size on students’ academic performance: empirical evidence for Andalusia

DOI: 10.4438/1988-592X-RE-2022-395-516

Luis Alejandro López-Agudo

Oscar David Marcenaro-Gutiérrez

Universidad de Málaga

Resumen

El tamaño de la clase ha sido y continúa siendo un foco del debate educativo en España. La mayoría de la literatura indica que existe una influencia negativa de las aulas sobrepobladas sobre el rendimiento académico de los estudiantes, lo que ha aumentado la creencia de que un tamaño de clase reducido favorecería el aprendizaje del alumnado. Sin embargo, la endogeneidad que presenta el tamaño de clase ha evitado que gran parte de los estudios –la mayoría correlacionales– obtengan su influencia real. En consecuencia, pretendemos resolver este problema mediante el uso de un procedimiento de regresión discontinua difusa (una combinación de regresión discontinua y variables instrumentales) usando como instrumento el tamaño de clase que los colegios deberían haber fijado si hubieran seguido la legislación educativa. Esta cuestión se ha estudiado para la región más poblada de España, esto es, Andalucía, usando datos censales para estudiantes de educación primaria y secundaria, proporcionados por la Agencia Andaluza de Evaluación Educativa (AGAEVE) para los cursos académicos 2011/12 y 2012/13. Nuestros resultados muestran que el tamaño de clase no influye en las calificaciones (en lectura y matemáticas) de los estudiantes de primaria y secundaria, y que las características de los estudiantes que componen la clase serían más importantes.

Palabras clave: tamaño de clase, rendimiento académico, regresión discontinua difusa, variables instrumentales, educación primaria, educación secundaria.

Abstract

Class size has been and continues to be a focus of the Spanish education debate. Most of the literature points towards the negative influence that overcrowded classes may have on students’ academic performance, which has increased the belief that a reduced class size may be better for students’ learning. However, the endogeneity that class size presents has prevented a great part of the research works – which are mostly correlational – to grasp its actual influence. Because of that, we intend to solve this issue by the use of a fuzzy regression discontinuity approach (a combination of regression discontinuity and instrumental variables) using as instrument the class size which schools should have set if they had followed the education legislation. This issue has been analysed for the most populated Spanish region, i.e. Andalusia, using census data for primary and secondary education students, provided by the Andalusian Agency of Education Assessment (AGAEVE) for the academic years 2011/12 and 2012/13. Our results show that class size does not influence students’ administrative scores (in mathematics and reading) in primary and secondary education and that the characteristics of the students in the class may be more important.

Keywords: class size, academic performance, fuzzy regression discontinuity, instrumental variables, primary education, secondary education.

1. Introducción

Existe un debate mundial sobre la influencia que puede tener el tamaño de la clase en el rendimiento académico de los estudiantes. La mayor parte de esta literatura parece indicar que una reducción en el tamaño de la clase afecta positivamente a los resultados académicos de los estudiantes (Argaw y Puhani, 2018; Bowne, Magnuson, Schindler, Duncan y Yoshikawa, 2017; Dolton y Marcenaro-Gutierrez, 2011; Goldstein, Yang, Omar, Turner y Thompson, 2000; Hanushek, 2002; Krueger, 2003; Shin y Young, 2009; Uttl, Bell y Banks, 2018, entre otros). A pesar de su relevancia, esta cuestión ha sido poco estudiada para España y, entre los pocos ejemplos disponibles, solo existe evidencia correlacional (como por ejemplo en Anghel y Cabrales, 2014). No obstante, a pesar de la falta de un cuerpo sólido de investigación empírica sobre el impacto del tamaño de la clase en España, se han implementado algunas políticas educativas para cambiar este límite. En particular, para la educación primaria y secundaria, hasta el curso 2011/12 el tamaño de la clase se fijó en 25 y 30 estudiantes (respectivamente) pero, en el siguiente curso académico, se incrementó en un 20% y se redujo nuevamente a 25 y 30 estudiantes en 2016.

En este contexto de cambios “arbitrarios” en el tamaño de las clases, la prensa española ha alertado sobre los problemas de las aulas sobrepobladas en cuanto al aprendizaje de los estudiantes, pues una elevada cantidad de estudiantes puede incrementar las interrupciones y el tiempo del profesorado para realizar tareas como calificar deberes o exámenes, reduciendo también el tiempo de aprendizaje que tienen los estudiantes2. Adicionalmente, disminuir el número de estudiantes por aula puede suponer un aumento en el número de grupos, lo que podría traducirse en la contratación de más docentes y, por tanto, mayores gastos presupuestarios destinados a los sueldos de estos docentes. Por ejemplo, siguiendo el MECD (2018), el profesorado de educación secundaria en España recibe 61.543$ (PPA) como salario máximo, que es un 7,4% más que la OCDE y un 7,8% más que la UE22. Por tanto, en este contexto, la decisión de reducir el tamaño de las clases en España no debería ser arbitraria, sino que debería estar basada en una contrastación empírica sólida.

En concreto, esta investigación analiza la influencia del tamaño de la clase sobre el rendimiento de los estudiantes de la región española más poblada (Andalucía, con un total de 8,4 millones de personas en 2018) que, además, es una de las regiones españolas con peor desempeño en las pruebas internacionales de evaluación a gran escala. En el caso de PISA3 2015 (OCDE, 2016), los estudiantes andaluces obtuvieron 479 puntos en lectura (a diferencia de los estudiantes españoles, que obtuvieron 496 puntos y 487 los de la OCDE), 466 en matemáticas (frente a 486 de España y 478 los de la OCDE) y 473 en ciencia (493 para España y 488 los de la OCDE). Además, Andalucía también presenta un alto porcentaje de estudiantes repetidores en PISA 2015 (38%), mientras que esta cifra fue del 31% para España y del 13% para la OCDE (OCDE, 2016). Esta situación se ha mantenido similar en PISA 2018 (MECD, 2019, 2020).

Este trabajo de investigación es novedoso ya que es la primera vez que se analiza la influencia del tamaño de la clase en el rendimiento académico de los estudiantes en España utilizando datos censales, junto con una metodología (regresión discontinua difusa) que nos permite acercarnos lo más posible a una influencia causal. En particular, la pregunta de investigación que queremos responder es:

¿Influye el tamaño de la clase en el rendimiento académico de los estudiantes de educación primaria y secundaria en Andalucía?

El resto del artículo está estructurado de la siguiente manera. En primer lugar, presentamos una breve revisión de la literatura, seguida de una descripción de los datos y la metodología empleada, los resultados, su discusión y conclusiones.

2. Revisión de la literatura

Según la literatura previa, el experimento educativo más famoso que estudió la influencia del tamaño de la clase sobre el rendimiento académico de los estudiantes fue el proyecto Tennessee Student Teacher Achievement Ratio (STAR). Numerosos autores, como Mosteller (1995) y Finn y Achilles (1999), analizaron sus resultados y destacaron que la reducción del tamaño de las clases era positiva para el rendimiento académico de los estudiantes de educación primaria, siendo aún más efectivo para los estudiantes pobres. Ehrenberg, Brewer, Gamoran y Willms (2001) analizaron este proyecto e indicaron que, aunque tenía validez interna, no tenía validez externa, ya que los resultados se aplicaban solo a los estudiantes participantes en el experimento, siendo las características de estos estudiantes diferentes de las presentadas por la población de estudiantes de Tennessee. Además, indicaron que la reducción del tamaño de las clases podría estar condicionada por la capacidad de los colegios para crear más clases.

Esta influencia positiva de la reducción del tamaño de la clase en el rendimiento académico de los estudiantes también fue resaltada por autores como Jepsen y Rivkin (2009), quienes analizaron un experimento destinado a estudiar la influencia del tamaño de la clase en el rendimiento académico de los estudiantes en la educación primaria en California, encontrando que una reducción del tamaño era positivo para el rendimiento académico en lectura y matemáticas. De manera similar, Breton (2014) encontró, para los estudiantes colombianos de cuarto grado en TIMSS4 2007, que una reducción de 53 a 20 estudiantes por clase aumentaba el rendimiento académico de los estudiantes en matemáticas en 0,80 desviaciones estándar. Francis y Barnett (2019) también analizaron este tema para los estudiantes de preescolar en Chicago, encontrando que una reducción de 5 estudiantes por clase hasta un total de 15 estudiantes elevó las puntuaciones cognitivas en lectura de los estudiantes en 0,2 desviaciones estándar. De hecho, algunos trabajos como Whitmore (2014) indicaron que un tamaño de clase reducido era necesario para obtener mejores resultados de los estudiantes, aunque esta influencia positiva se redujo para los grados más altos. Zyngier (2014) analizó 112 trabajos de investigación y también indicó que la influencia positiva de la reducción del tamaño de la clase en los resultados académicos de los estudiantes puede ser más relevante en los primeros grados, e incluso mayor para los estudiantes de entornos socioeconómicos desaventajados. Por el contrario, Etim, Etim y Blizard (2020) analizaron la influencia del tamaño de la clase en los estudiantes de primaria y secundaria en Carolina del Norte, encontrando que la influencia de un tamaño de clase más grande era negativa en la educación primaria, pero positiva en la educación secundaria.

Algunos meta-análisis también han estudiado este tema. Por ejemplo, Goldstein et al. (2000) se centró en 9 trabajos de investigación que utilizaron análisis multinivel y encontraron una reducción del rendimiento académico de los estudiantes en 0,02 desviaciones estándar por cada estudiante adicional en la clase. De forma similar, Finn, Pannozzo y Achilles (2003) realizaron una revisión de la literatura sobre el tamaño de la clase y encontraron que un tamaño reducido de ésta se asoció con una mayor participación de los estudiantes, que también se asoció con su rendimiento académico. Shin y Young (2009) realizaron un meta-análisis de 17 estudios para los Estados Unidos y encontraron que las clases pequeñas presentaban resultados académicos de 0,20 desviaciones estándar más altos que los de las clases más grandes. En una línea similar, Bowne et al. (2017) analizaron 38 estudios sobre la influencia del tamaño de las clases para los estudiantes de primera infancia en Estados Unidos, encontrando una influencia positiva de un tamaño de clase más bajo que varió de 0,22 a 0,10 desviaciones estándar hasta los 15 estudiantes por clase, siendo esta influencia nula para clases más grandes. Filges, Sonne-Schmidt, y Nielsen (2018) realizaron un meta-análisis de 127 estudios para 41 países, para estudiantes desde guardería hasta el doceavo grado, encontrando una influencia positiva pero pequeña de la reducción del tamaño de la clase sobre el rendimiento en lectura de los estudiantes, pero sin influencia para las matemáticas. Además, Uttl et al. (2018) realizó un meta-análisis utilizando más de 100 estudios, encontrando que un tamaño de clase reducido era positivo para el rendimiento académico de los estudiantes hasta 20 estudiantes por clase, disminuyendo esta influencia de 20 a 30 estudiantes por clase.

Por otro lado, algunos trabajos de investigación han indicado que “reducir el tamaño de la clase no es, por sí sola, una herramienta política suficiente para mejorar el desempeño de los sistemas educativos, y es una medida menos eficiente que aumentar la calidad de la enseñanza” (OCDE, 2012, p.1). Chingos y Whitehurst (2011) también apoyaron este argumento, encontrando que la mayoría de los estudios existentes sobre el tamaño de las clases, a pesar de su gran cantidad, no logran tener la calidad suficiente para ser la base de políticas educativas. Esto también fue apoyado por Hanushek (2011), quien indicó que la calidad del profesorado parece ser más importante que el tamaño de la clase. Li y Konstantopoulos (2017) utilizaron datos de TIMSS 2011 para estudiantes de cuarto grado en 14 países europeos, y también encontraron que el tamaño de la clase puede no tener una influencia positiva en el rendimiento académico de los estudiantes (con la excepción de Eslovaquia), indicando que la dinámica del aula, la instrucción y las prácticas pueden ser relevantes para explicar el desempeño académico, pero que no pudieron ser controladas en el modelo, pues estas variables no se incluyeron en la base de datos. Leuven y Løkken (2017) analizaron la influencia del tamaño de la clase para los estudiantes de primer a noveno grado en Noruega, y también encontraron que el tamaño de la clase puede no ser relevante para explicar su rendimiento académico. De manera similar, Köhler (2020) analizó este tema para estudiantes sudafricanos de doceavo grado, encontrando una influencia nula del tamaño de la clase en el rendimiento académico, lo que indica que otras características como las de los docentes o la funcionalidad escolar podrían ser más relevantes.

Por lo tanto, la mayoría de los estudios parecen fallar en obtener una influencia causal del tamaño de la clase sobre el rendimiento académico de los estudiantes debido a la endogeneidad y problemas de omisión de variables. Algunos trabajos de investigación que lo han logrado con éxito son, por ejemplo, Akerhielm (1995), quien empleó un enfoque de variables instrumentales, utilizando el tamaño promedio de la clase para una materia en particular y la cantidad de estudiantes de octavo grado en Estados Unidos como instrumentos. Encontró que la influencia del tamaño de la clase en el rendimiento académico de los estudiantes cambiaba de positiva (estimando con mínimos cuadrados ordinarios) a negativa (pero pequeña) o insignificante cuando se usaba una estimación con variables instrumentales. Otros trabajos de investigación como Angrist y Lavy (1999) se han acercado a esta relación causal, utilizando un enfoque de regresión discontinua difusa para estudiantes israelíes de cuarto y quinto grado, encontrando que un tamaño de clase reducido mejoraba su rendimiento académico. En este estudio seguimos un enfoque similar, pero para estudiantes españoles de cuarto y octavo grado, usando las observaciones de los estudiantes en lugar de las observaciones de la clase. Estos autores revisaron su análisis en Angrist, Lavy, Leder-Luis y Shany (2019), utilizando datos de estudiantes israelíes de quinto grado, para el período 2002-2011, y no encontraron ninguna evidencia de que el tamaño de la clase influyera en el rendimiento académico de los estudiantes. Shen y Konstantopoulos (2019) también emplearon un enfoque de regresión discontinua difusa en los datos de TIMSS 2003, 2007 y 2011 para analizar la influencia del tamaño de la clase sobre el rendimiento de los estudiantes de octavo grado en Hungría, Lituania, Rumania y Eslovenia, encontrando que una reducción de 1 estudiante por clase en Rumania se asoció positivamente con un aumento de 0,05 desviaciones estándar en las puntuaciones de matemáticas y ciencias, y 0,03 desviaciones estándar en las puntuaciones de ciencias para Lituania; sin embargo, el tamaño de la clase no influyó en el rendimiento académico de los estudiantes en Hungría y Eslovenia.

Blatchford (2016) indicó que la comparación entre países en términos de tamaño de clase podría ser engañosa, debido a la baja validez externa de algunos trabajos de investigación, por lo que se debe prestar especial atención a la situación de cada país. Siguiendo esta lógica, el presente trabajo de investigación se centra en España y, en concreto, en Andalucía. Esto es particularmente relevante, teniendo en cuenta que la evidencia sobre la influencia del tamaño de la clase sobre el rendimiento académico de los estudiantes en España es bastante escasa, correlacional y lejos de ser concluyente. Por ejemplo, Wößmann y West (2006) encontraron una asociación positiva entre la reducción del tamaño de la clase y el rendimiento académico de los estudiantes españoles de octavo grado (utilizando datos de TIMSS 1995); sin embargo, emplearon como instrumento el tamaño promedio de la clase indicado por el/la director/a del colegio, por lo que podría estar sujeto a error. Otros autores como Mora, Escardíbul y Espasa (2010) analizaron una reforma de la política educativa, implementada en España entre 1992 y 2003, y su influencia sobre las tasas de abandono del grupo de edad de 18 a 24 años (a partir de datos del Ministerio de Educación español y un modelo logístico correlacional), encontrando que un tamaño de clase reducido disminuyó las tasas de abandono educativo en alrededor de 0,4% por estudiante en la clase. De manera similar, García-Pérez, Hidalgo-Hidalgo y Robles-Zurita (2014) emplearon un modelo de regresión switching y encontraron, para los estudiantes de 15 años que participaron en PISA 2009, que un tamaño reducido de clase se asoció positivamente con el rendimiento académico de los no repetidores en matemáticas (en 0,008 desviaciones estándar por cada estudiante menos en la clase) pero con rendimientos decrecientes. Por el contrario, Anghel y Cabrales (2014) analizaron un censo de estudiantes de sexto de primaria en el curso académico 2008/09 en Madrid, utilizando una regresión por mínimos cuadrados ordinarios y efectos fijos de colegio; indicaron que el tamaño de la clase no parecía influir sobre el rendimiento académico de los estudiantes, por lo que concluyeron que las políticas centradas en éste podrían ser un desperdicio de recursos.

3. Datos y metodología

3.1. Datos

La base de datos censal empleada en el presente trabajo fue recopilada y proporcionada por la Agencia Andaluza de Evaluación Educativa (AGAEVE en adelante) con el objetivo de medir las competencias (o habilidades cognitivas) de los estudiantes en una evaluación denominada “prueba de evaluación diagnóstica”. Concretamente, esta evaluación pretende medir las competencias de los estudiantes en lengua española (lectura a partir de ahora) y matemáticas, siendo estas pruebas puntuadas por profesorado externo. Estas pruebas se desarrollaron utilizando preguntas que eran similares en su estructura y propósito a las empleadas por PISA para medir las competencias de los estudiantes5. Además, los estudiantes están vinculados a sus calificaciones (puntuaciones SENECA) que son las puntuaciones que obtuvieron en las materias de lectura y matemáticas en el colegio después de terminar el curso académico (calificadas por los docentes), es decir, miden el conocimiento de contenidos de los estudiantes; estas calificaciones se utilizarán como variable dependiente en el presente estudio. Además, esta evaluación diagnóstica contiene cuestionarios del estudiante, la familia, el/la tutor/a y el colegio (respondido por el/la directora/a), y también contiene información sobre el tamaño de cada clase dentro de cada colegio.

Los datos utilizados en esta investigación son los del curso académico 2012/13 para estudiantes de cuarto y octavo grado, junto con los datos de octavo grado para el curso académico 2011/12 (que usaremos para verificar la robustez de los resultados de educación secundaria)6. Estos dos cursos se utilizan porque el gobierno español aumentó en un 20% el límite de tamaño de la clase7 desde el límite inicial de 25 estudiantes para educación primaria (primero a sexto grado) y el límite de 30 estudiantes para educación secundaria (séptimo a décimo grado) en 2011/12 a 30 estudiantes en educación primaria y 36 estudiantes en educación secundaria en 2012/13. En este conjunto de datos censales hay un total de 90.048 estudiantes en 2.482 colegios en cuarto grado en 2012/13, 86.626 estudiantes en 1.595 colegios en octavo grado en 2012/13 y 88.277 estudiantes en 1.609 colegios en octavo grado en 2011/12.

3.2. Metodología

Primero, con el objetivo de desarrollar la metodología de regresión discontinua difusa, necesitamos verificar algunas características de nuestros datos:

3.2.1. Contraste de variación exógena

Como se indicó anteriormente, la legislación educativa indicó que los colegios debían alcanzar un máximo de 30 estudiantes por clase en educación primaria y 36 en educación secundaria en el curso 2012/13 (30 estudiantes por clase en educación secundaria en el curso 2011/12). Esta legislación se estableció de manera exógena, pero los/as directores/as de los colegios podían decidir seguirla o no en función de algunas variables condicionales, por lo que no es tan exógena como debería ser (en nuestros datos, solo el 38,18% de las clases en cuarto grado y el 17% en octavo grado8 en 2012/13 la siguió estrictamente)9. Éste es el principal problema que nos hace utilizar un enfoque de regresión discontinua difusa (que combina la regresión discontinua con variables instrumentales) en lugar de utilizar directamente una metodología de regresión discontinua nítida, como explicaremos a continuación.

3.2.2. Contraste de discontinuidad en las covariables

Con el fin de seleccionar la muestra para nuestra estrategia de regresión discontinua difusa, obtuvimos el número total de estudiantes que asistían a cuarto y octavo grado en cada colegio y curso académico (lo que llamamos el “tamaño del colegio”). Luego, siguiendo a Angrist y Lavy (1999), tomamos aquellos colegios que tenían un tamaño de colegio de ± 5 estudiantes alrededor de la cifra límite que fijaba la legislación de tamaño de clase para ese curso académico. Por ejemplo, en 2012/13 la legislación sobre el tamaño de las clases para la educación primaria (y para educación secundaria en 2011/12) indicó un máximo de 30 estudiantes por clase, por lo que mantuvimos los colegios que tenían de 26 a 35 estudiantes, 56 a 65, 86 a 95, 116 a 125, 146 a 155 y 176 a 185 estudiantes10.

Los principales estadísticos descriptivos se presentan en la Tabla A1 (Anexo) para cada grado y curso académico, junto con un contraste de diferencia de medias entre la población y la muestra analizada. En estos estadísticos podemos apreciar algunas diferencias significativas entre ambas en cuanto a las características socioeconómicas de los estudiantes y la financiación escolar, con un mayor número de diferencias para octavo grado en ambos cursos académicos (muy probablemente debido al menor porcentaje de clases que siguieron la legislación de tamaño de las clases). Por lo tanto, esto puede ser el resultado, nuevamente, de una decisión no aleatoria de los colegios sobre el tamaño de su clase, por lo que se incluirán variables de control del estatus socioeconómico11 de los estudiantes y la financiación escolar a nuestras estimaciones para capturar estas diferencias.

3.2.3. Contraste de continuidad de la densidad y del instrumento del tamaño de clase

A continuación, describimos la creación de un instrumento de tamaño de clase que intentará resolver la anteriormente descrita posible asignación no aleatoria de estudiantes a las clases. En este caso, el instrumento propuesto es el tamaño de clase que los colegios deberían haber establecido cuando su tamaño de colegio alcanzó el límite de tamaño indicado por la ley, distribuyendo así al azar a los estudiantes en clases de igual tamaño. Para obtener este instrumento, seguimos a Angrist y Lavy (1999) y calculamos:

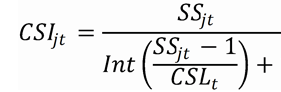(1)

donde j es el colegio; t el grado y el curso académico (t = 1 para cuarto grado en 2012/13, t = 2 para octavo grado en 2012/13 y t = 3 para octavo grado en 2011/12); SSjt es el tamaño del colegio en ese grado y curso académico en particular; CSLt es el límite de tamaño de la clase por ley para ese grado y curso académico (tomando el valor 30 para cuarto grado en 2012/13 –y también para octavo grado en 2011/12– y 36 para octavo grado en 2012/13); para cualquier número positivo n, la función Int(n) es el entero más grande menor o igual que n. Por ejemplo, para cuarto grado en el curso académico 2012/13 y tamaños de colegio entre 1 y 30, CSIjt toma los valores [1-30], [15,5-30] para tamaños de colegio entre 31-60, [20,33-30] para 61-90, [22,75-30] para 91-120, y así sucesivamente. Concretamente, este instrumento de tamaño de clase muestra el tamaño de clase que debería haberse establecido en el caso de que los colegios hubieran seguido exactamente la legislación cuando su tamaño de colegio alcanzó el límite de tamaño de clase. Por ejemplo, siempre que el tamaño del colegio llega a 32 en cuarto grado en 2012/13 (2 estudiantes por encima del límite), los estudiantes deberían haber sido separados al azar en dos clases de 16 estudiantes. Por lo tanto, en la medida en que este instrumento de tamaño de clase se basa en una regulación exógena para el tamaño de clase, nuestro instrumento seguirá el supuesto de independencia/exogeneidad.

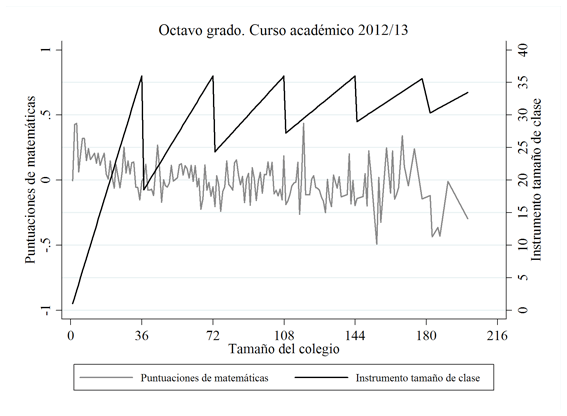
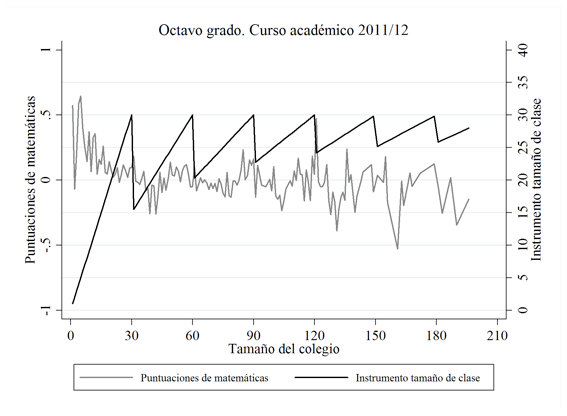
A continuación, presentamos algunos gráficos para analizar la relación entre el tamaño de la clase y nuestro instrumento de tamaño de clase (Figura 1), tanto para el cuarto como para el octavo grado en 2012/13 (y el octavo grado en 2011/12). Como se puede apreciar (y se indicó anteriormente), parece que los colegios no siguen exactamente la legislación en el sentido de dividir a sus estudiantes en clases de tamaño similar cuando el tamaño del colegio alcanza el límite de tamaño de clase. El tamaño real de la clase y el instrumento de tamaño de la clase presentan una correlación significativa de 0,77 en cuarto grado y de 0,41 en octavo grado en 2012/13 (0,50 en octavo grado en 2011/12) por lo que, como análisis preliminar, parece que este instrumento puede estar suficientemente correlacionado con la variable endógena que instrumenta, cumpliendo con el supuesto de relevancia (necesitando también un contraste de instrumentos débiles de Stock y Yogo, 2005, para comprobar esto, como veremos en la sección de Resultados).

FIGURA 1. Relación entre el tamaño de la clase y el instrumento de tamaño de la clase

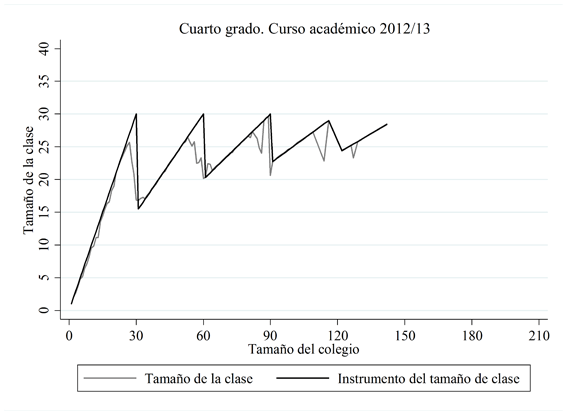
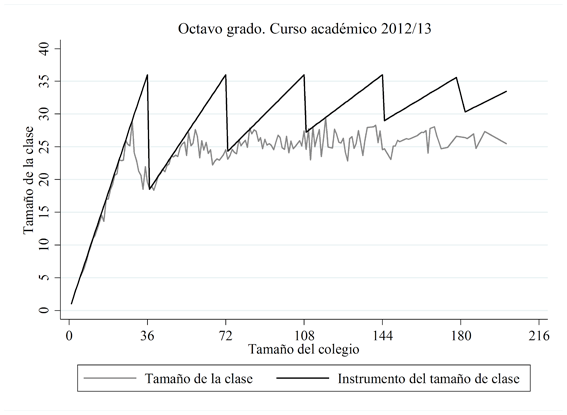
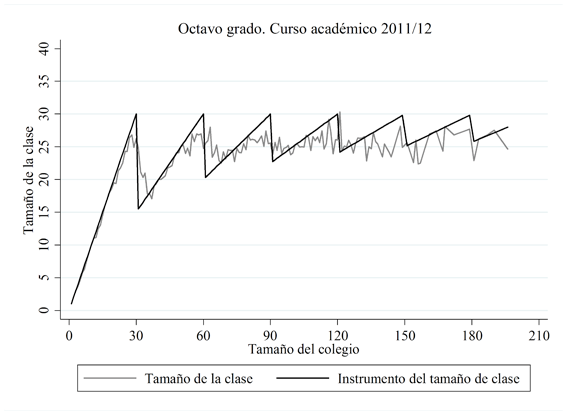
Notas: El tamaño de la clases se ha calculado por tamaño del colegio.

Fuente: Elaboración propia.

3.2.4. Contraste de discontinuidad de las variables dependientes

Como indican Feir, Lemieux y Marmer (2016), necesitamos que la discontinuidad de las variables dependientes no sea débil para que nuestra estrategia de identificación funcione. Para verificar esto, hemos representado la relación entre las calificaciones estandarizadas en lectura (Figura 2) y matemáticas (Figura 3), tanto para el cuarto como para el octavo grado en 2012/13 (y el octavo grado en 2011/12), junto con el instrumento del tamaño de la clase. Parece que existe una relación positiva entre el instrumento del tamaño de clase y las calificaciones de los estudiantes (contrariamente a lo que se encuentra en la literatura), en la medida en que las calificaciones estandarizadas parecen imitar el comportamiento del instrumento del tamaño de clase, incluso en los “valles” (o caídas) de los puntos de corte del instrumento del tamaño de clase. Esta correlación parece indicar que nuestra estrategia de regresión discontinua puede funcionar (si el instrumento del tamaño de clase no está correlacionado con el término de error; comprobaremos esto cuando apliquemos el contraste de endogeneidad de Wooldridge, 1995, en la sección de Resultados).

FIGURA 2. Relación entre el instrumento del tamaño de clase y las calificaciones estandarizadas de lectura

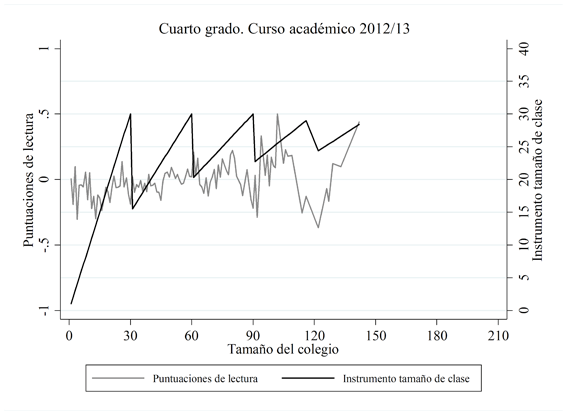
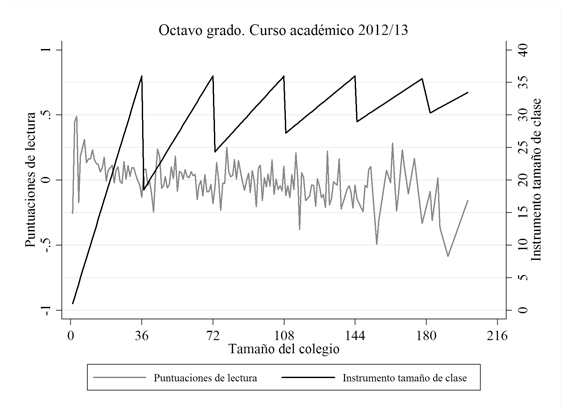
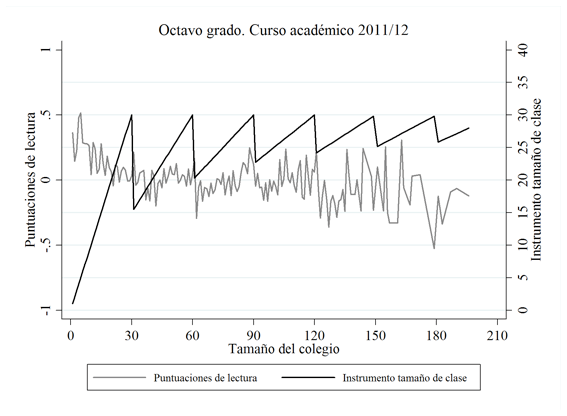
Notas: Las calificaciones estandarizadas de lectura se han calculado por tamaño del colegio.

Fuente: Elaboración propia.

FIGURA 3. Relación entre el instrumento del tamaño de clase y las calificaciones estandarizadas de matemáticas

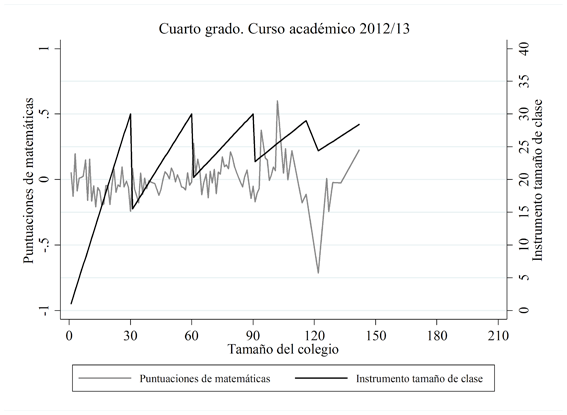
Notas: Las calificaciones estandarizadas de matemáticas se han calculado por tamaño del colegio.

Fuente: Elaboración propia.

Hay dos propiedades adicionales que nuestro instrumento de tamaño de clase debe presentar. Primero, la restricción de exclusión, que establece que el único canal de influencia del instrumento sobre el rendimiento académico de los estudiantes es a través del tamaño de la clase. Como hemos visto anteriormente, el instrumento parece cumplir con esta restricción, ya que parece estar relacionado con las variables dependientes (como se encuentra en las Figuras 2 y 3) y los posibles factores que pueden confundir esta relación pueden ser controlados tanto por el uso de la regresión discontinua difusa como por controles de estatus socioeconómico. La segunda es la propiedad de monotonicidad (Barua y Lang, 2016; Dhuey, Figlio, Karbownik y Roth, 2019; o Fiorini y Stevens, 2014). Barua y Lang (2016, p. 348) la definieron como “si bien el instrumento puede no tener efecto en algunos/as individuos/as, todos/as los/as afectados/as deberían verse afectados/as unidireccionalmente”12. Por lo tanto, a la vista de los resultados anteriores, parece que se cumple la propiedad de monotonicidad, ya que parece haber una tendencia creciente en las calificaciones estandarizadas con el instrumento de tamaño de clase, que comienza siempre que se llega a un límite de tamaño de clase.

3.2.5. Mínimos cuadrados ordinarios y estimaciones censales

Para ver cómo el uso de un enfoque de regresión simple puede sesgar nuestros resultados presentamos la Tabla I. En esta tabla se ha empleado la información censal, analizando la influencia del tamaño de clase (especificación I) y la de nuestro instrumento de tamaño de clase (especificación II) sobre las calificaciones estandarizadas de los estudiantes. Como se puede apreciar, esta influencia es positiva en el caso de la variable de tamaño de clase, pero difiere en función del grado y curso académico para el instrumento de tamaño de clase (que va de negativa a positiva). Por lo tanto, podemos ver aquí que, en el primer caso, la omisión de variables relevantes que explican las calificaciones estandarizadas de los estudiantes puede sesgar positivamente la influencia del tamaño de clase. En el segundo caso, el uso del instrumento del tamaño de clase, que representa una división “adecuada” de las clases, está libre de esta omisión; sin embargo, aunque sea ideal para nuestro trabajo de investigación, esta última división no refleja la realidad.

TABLA I. Influencia del tamaño de clase en las calificaciones estandarizadas de los estudiantes, estimaciones para la población

	Cuarto grado. 2012/13				Octavo grado. 2012/13				Octavo grado. 2011/12
	Especificación I		Especificación II		Especificación I		Especificación II		Especificación I		Especificación II
Variables	Lectura	Matemáticas	Lectura	Matemáticas	Lectura	Matemáticas	Lectura	Matemáticas	Lectura	Matemáticas	Lectura	Matemáticas
Tamaño de clase	0,013***	0,010***	-	-	0,017***	0,017***	-	-	0,016***	0,016***	-	-
	(0,002)	(0,002)			(0,002)	(0,002)			(0,002)	(0,002)
Instrumento de tamaño de clase	-	-	0,009***	0,006***	-	-	-0,008***	-0,007***			-0,003	-0,002
			(0,002)	(0,002)			(0,002)	(0,002)			(0,002)	(0,002)
Constante	-0,297***	-0,226***	-0,219***	-0,130***	-0,420***	-0,407***	0,236***	0,205***	-0,397***	-0,376***	0,064	0,057
	(0,037)	(0,035)	(0,039)	(0,038)	(0,039)	(0,040)	(0,041)	(0,043)	(0,043)	(0,042)	(0,053)	(0,054)
Observaciones	88.909	88.905	88.909	88.905	85.915	85.920	85.915	85.920	86.600	86.596	86.600	86.596
R-cuadrado	0,003	0,002	0,002	0,001	0,008	0,007	0,002	0,001	0,007	0,006	0,000	0,000

Notas: Errores estándar entre paréntesis y clusterizados a nivel de distrito.

Método de estimación: Mínimos cuadrados ordinarios.

Variable dependiente: Calificaciones estandarizadas usando la media y desviación típica de la población.

Coeficiente: *** Significativo al 1%, ** significativo al 5%, * significativo al 10%.

Fuente: Elaboración propia.

Por lo tanto, tenemos que pasar a nuestro enfoque de regresión discontinua difusa para acercarnos a la influencia del tamaño de la clase sobre el rendimiento académico de los estudiantes.

3.2.6. Regresión discontinua difusa

Una vez definido nuestro instrumento de tamaño de clase, podemos implementar la metodología de regresión discontinua difusa. Para hacer esto, nos ceñimos solo a nuestra muestra de análisis (colegios que tenían un tamaño de colegio de ± 5 estudiantes alrededor de la cifra de la legislación para ese curso académico) y estimamos el siguiente modelo, por separado para cada curso académico:

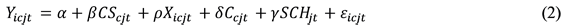
donde i representa al estudiante, c la clase, j el colegio y t el grado y el curso académico (t = 1 para el cuarto grado en 2012/13, t = 2 para el octavo grado en 2012/13 y t = 3 para el octavo grado en 2011/12); Yicjt son las calificaciones estandarizadas de los estudiantes (en lectura o matemáticas)13; CScjt es el tamaño de la clase; Xicjt son las características observables de los estudiantes; Ccjt son las características observables de la clase; SCHjt son las características observables del colegio; a es un término constante y εicjt es el término de error idiosincrásico.

Como se argumentó anteriormente, nuestra variable de interés (CScjt) puede estar sesgada por la decisión particular de cada director/a de colegio en términos de división de clases. Por eso, estimamos nuestro modelo principal mediante el uso de mínimos cuadrados ordinarios en dos etapas, para cada grado y curso académico. Nuestro instrumento es el CSIjt previamente definido. La idea subyacente es instrumentalizar la variable de tamaño de clase utilizando, como instrumento, el tamaño de clase que los colegios deberían haber fijado si hubieran seguido la legislación educativa, junto con el resto de variables que pueden explicar las diferencias entre estos dos tamaños de clase. Por lo tanto, en la primera etapa de este procedimiento, especificamos una regresión de la variable de tamaño de clase explicada por el instrumento de tamaño de clase y estas variables:

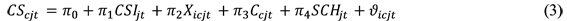
Donde π son los coeficientes de las variables controladas y ϑicjt el término de error idiosincrásico. Una vez controladas estas variables, podemos obtener el valor predicho del tamaño de la clase a partir de la ecuación (3), es decir , que estaría libre de la influencia de estas variables. A continuación, podemos continuar con la segunda etapa, en la que sustituimos CScjt de la ecuación (2) por este valor predicho ():

El coeficiente β mediría la influencia del tamaño de la clase en las calificaciones estandarizadas de los estudiantes. El hecho de que este coeficiente mida nuestra influencia de interés depende de la identificación de aquellas variables que hacen que CScjt difiera de CSIjt. Por lo tanto, hemos controlado por las características de los estudiantes (Xicjt) como el sexo, estatus socioeconómico y competencias (en lectura o matemáticas). En el caso de las variables de clase (Ccjt), hemos controlado por los años de experiencia del/la profesor/a tutor/a – como indicaron Breton (2014) o Hanushek (2011), esta experiencia puede condicionar la influencia del tamaño de la clase en el rendimiento académico de los estudiantes. Con respecto a las variables del colegio (SCHjt), hemos controlado por la financiación del colegio y el tamaño del colegio. También se ha controlado por el tamaño del colegio al cuadrado, con el fin de encontrar posibles no linealidades. Como comprobación de la robustez de nuestros resultados y siguiendo a Angrist y Lavy (1999), también hemos empleado una variable de tamaño de colegio “por partes”14. Además, hemos añadido una variable de tamaño de distrito y la muestra se ha clusterizado por distrito, para tener en cuenta las posibles diferencias entre distritos en la cantidad de estudiantes que pueden acceder a los colegios.

4. Resultados

Los principales resultados de nuestro análisis de regresión discontinua difusa se presentan en la Tabla II. Primero, en la especificación I hemos incluido como controles solo el tamaño de la clase, el tamaño del colegio y el tamaño colegio al cuadrado, encontrando que el tamaño de la clase no parece tener ninguna influencia en las calificaciones estandarizadas de los estudiantes en ninguno de los casos. Luego, en la especificación II hemos incluido el resto de controles descritos anteriormente. Como se puede apreciar, nuevamente, el tamaño de la clase parece tener una influencia nula en las calificaciones de los estudiantes. En cuanto al resto de variables, hay algunas que pueden ser más importantes que el tamaño de la clase para explicar las calificaciones estandarizadas de los estudiantes: las niñas parecen rendir mejor que los niños en alrededor de 0,03 y 0,10 desviaciones estándar (DE) en cuarto grado y entre 0,16 a 0,20 DE en octavo grado; en el caso del estatus socioeconómico de los estudiantes, también tiene una influencia positiva en las calificaciones estandarizadas de los estudiantes (alrededor de 0,23 DE en cuarto grado y entre 0,14 a 0,18 DE en octavo grado por cada aumento de 1 DE en este índice). Además, las competencias estandarizadas de los estudiantes tienen una influencia positiva en las calificaciones estandarizadas de los estudiantes: alrededor de 0,58 DE en cuarto grado y entre 0,49 a 0,58 DE en octavo grado, por cada aumento de 1 DE en las competencias de los estudiantes15.

TABLA II. Influencia del tamaño de clase en las calificaciones estandarizadas de los estudiantes

	Especificación I						Especificación II
	Cuarto grado. 2012/13		Octavo grado. 2012/13		Octavo grado. 2011/12		Cuarto grado. 2012/13		Octavo grado. 2012/13		Octavo grado. 2011/12
Variables	Lectura	Matemáticas	Lectura	Matemáticas	Lectura	Matemáticas	Lectura	Matemáticas	Lectura	Matemáticas	Lectura	Matemáticas
Tamaño de clase	-0,001	-0,004	-0,018	0,018	0,022*	0,019	-0,022	-0,032	0,003	0,013	-0,011	-0,028
	(0,008)	(0,008)	(0,038)	(0,038)	(0,012)	(0,012)	(0,019)	(0,020)	(0,041)	(0,039)	(0,027)	(0,029)
Tamaño de colegio	0,004	0,006	0,003	-0,004	0,002	-0,001	0,005	0,007**	0,001	-0,002	0,005*	0,005
	(0,004)	(0,005)	(0,007)	(0,006)	(0,002)	(0,001)	(0,003)	(0,003)	(0,007)	(0,007)	(0,003)	(0,003)
Tamaño de colegio al cuadrado	-0,000	-0,000	-0,000	0,000	-0,000	0,000	-0,000	-0,000*	-0,000	0,000	-0,000**	-0,000
	(0,000)	(0,000)	(0,000)	(0,000)	(0,000)	(0,000)	(0,000)	(0,000)	(0,000)	(0,000)	(0,000)	(0,000)
Años de experiencia del/la tutor/a (Ref.: menos de 5 años)
20 años o más	-	-	-	-	-	-	-0,183***	-0,192***	0,047	0,006	-0,040	-0,028
							(0,049)	(0,047)	(0,054)	(0,062)	(0,032)	(0,036)
10 años o más y menos de 20	-	-	-	-	-	-	-0,144***	-0,161***	0,027	-0,025	0,012	-0,060*
							(0,055)	(0,054)	(0,052)	(0,062)	(0,033)	(0,035)
5 años o más y menos de 10	-	-	-	-	-	-	-0,078	-0,149***	0,050	-0,041	-0,002	0,003
							(0,051)	(0,050)	(0,048)	(0,056)	(0,031)	(0,033)
Financiación del colegio: (Ref.: público)
Privado	-	-	-	-	-	-	0,004	-0,032	0,612***	0,387***	0,081	0,226
							(0,167)	(0,127)	(0,153)	(0,143)	(0,153)	(0,198)
Concertado	-	-	-	-	-	-	0,050	0,166	-0,044	-0,156	-0,084	-0,019
							(0,141)	(0,150)	(0,171)	(0,178)	(0,158)	(0,168)
Tamaño del distrito							0,000	0,000	-0,000	-0,000*	-0,000**	-0,000
							(0,000)	(0,000)	(0,000)	(0,000)	(0,000)	(0,000)
Mujer (Ref.: varón)	-	-	-	-	-	-	0,101***	0,031***	0,156***	0,199***	0,179***	0,198***
							(0,013)	(0,012)	(0,016)	(0,014)	(0,011)	(0,013)
Estatus socioeconómico	-	-	-	-	-	-	0,228***	0,234***	0,175***	0,144***	0,164***	0,159***
							(0,012)	(0,013)	(0,023)	(0,023)	(0,016)	(0,017)
Competencias estandarizadas	-	-	-	-	-	-	0,582***	0,585***	0,486***	0,576***	0,524***	0,577***
							(0,013)	(0,012)	(0,027)	(0,024)	(0,018)	(0,019)
Constante	-0,072	-0,085	0,265	-0,253	-0,551**	-0,363	0,448	0,608*	-0,036	-0,106	0,089	0,464
	(0,194)	(0,216)	(0,563)	(0,585)	(0,272)	(0,289)	(0,344)	(0,364)	(0,554)	(0,523)	(0,470)	(0,511)
Observaciones	16.031	16.028	19.672	19.681	27.646	27.640	16.031	16.028	19.672	19.681	27.646	27.640
	Tests de variables instrumentales
Test de endogeneidad de Wooldridge (1995)	3,586*	4,420**	1,543	0,055	0,081	0,234	1,574	2,746	0,090	0,346	0,034	0,630
Test de instrumentos débiles de Stock y Yogo (2005)	78,927***	78,931***	5,450***	5,597***	22,551***	22,550***	18,185***	18,1892***	7,058***	6,728***	6,455***	6,380***

Notas: Errores estándar entre paréntesis y clusterizados a nivel de distrito. Una missing flag ha sido incluida para evitar información perdida en años de experiencia del/la tutor/a, estatus socioeconómico y competencias estandarizadas. La hipótesis nula del test de endogeneidad de Wooldridge (1995) es que la variable endógena es ahora exógena y la hipótesis nula del test de instrumentos débiles de Stock y Yogo (2005) es que el instrumento es débil.

Método estimación: Regresión discontinua difusa (regresión discontinua y mínimos cuadrados en dos etapas). El instrumento del tamaño de clase es el tamaño de clase que los colegios deberían haber fijado si hubieran seguido la legislación educativa.

Variable dependiente: Calificaciones estandarizadas usando la media y desviación típica de la población.

Coeficiente: *** Significativo al 1%, ** significativo al 5%, * significativo al 10%.

Fuente: Elaboración propia.

Podemos encontrar, en esta misma tabla, dos contrastes destinados a comprobar si nuestro instrumento ha resuelto los problemas de endogeneidad o no. Centrándonos en la especificación II, el primero es el test de endogeneidad de Wooldridge (1995), en el que la hipótesis nula es que la variable de tamaño de clase ya no es endógena; se acepta la hipótesis nula de este test, por lo que podemos confiar en que nuestro enfoque ha resuelto los problemas de endogeneidad. Luego, realizamos el test de Stock y Yogo (2005) de instrumentos débiles, con el fin de comprobar si el instrumento de tamaño de clase está suficientemente correlacionado con la variable endógena de tamaño de clase, siendo la hipótesis nula que es un instrumento débil. Como podemos apreciar, la hipótesis nula se rechaza al 1%, por lo que podemos asegurar que nuestro instrumento no es débil. Por lo tanto, los resultados de estos dos contrastes apoyan que nuestro instrumento de tamaño de clase funciona bien dentro de este enfoque de regresión discontinua difusa. En particular, para la especificación I en cuarto grado el primer test indica que nuestro instrumento no resuelve los problemas de endogeneidad; sin embargo, cuando se han controlado todas las posibles variables mediadoras de la diferencia entre el tamaño de la clase y su instrumento, parece que los problemas de endogeneidad se resuelven.

En el caso de nuestro análisis de robustez utilizando un tamaño de colegio por partes, los resultados se presentan en la Tabla III y también encontramos una influencia nula del tamaño de la clase en las calificaciones estandarizadas de los estudiantes y que nuestro instrumento también funciona.

TABLA III. Influencia del tamaño de clase en las calificaciones estandarizadas de los estudiantes, tamaño del colegio por partes

Variables	Cuarto grado. 2012/13		Octavo grado. 2012/13		Octavo grado. 2011/12
	Lectura	Matemáticas	Lectura	Matemáticas	Lectura	Matemáticas
Tamaño de clase	-0,022	-0,031	0,005	0,014	-0,003	-0,025
	(0,019)	(0,020)	(0,038)	(0,036)	(0,026)	(0,027)
Tamaño del colegio por partes	0,002	0,003	-0,002	-0,003	0,001	0,005
	(0,003)	(0,003)	(0,006)	(0,006)	(0,004)	(0,004)
Años de experiencia del/la tutor/a (Ref.: menos de 5 años)
20 años o más	-0,182***	-0,192***	0,045	0,007	-0,040	-0,028
	(0,048)	(0,047)	(0,052)	(0,060)	(0,031)	(0,036)
10 años o más y menos de 20	-0,147***	-0,165***	0,025	-0,025	0,007	-0,061*
	(0,055)	(0,053)	(0,050)	(0,060)	(0,033)	(0,034)
5 años o más y menos de 10	-0,079	-0,150***	0,048	-0,040	-0,006	0,001
	(0,051)	(0,050)	(0,047)	(0,056)	(0,030)	(0,033)
Financiación del colegio: (Ref.: público)
Privado	0,013	-0,019	0,598***	0,387***	0,030	0,204
	(0,162)	(0,121)	(0,158)	(0,148)	(0,146)	(0,186)
Concertado	0,044	0,158	-0,055	-0,160	-0,133	-0,040
	(0,137)	(0,146)	(0,162)	(0,169)	(0,154)	(0,157)
Tamaño del distrito	-0,000	-0,000	-0,000	-0,000*	-0,000**	-0,000
	(0,000)	(0,000)	(0,000)	(0,000)	(0,000)	(0,000)
Mujer (Ref.: varón)	0,101***	0,031***	0,157***	0,199***	0,179***	0,198***
	(0,013)	(0,012)	(0,015)	(0,014)	(0,011)	(0,013)
Estatus socioeconómico	0,228***	0,235***	0,175***	0,144***	0,164***	0,159***
	(0,012)	(0,013)	(0,024)	(0,023)	(0,016)	(0,016)
Competencias estandarizadas	0,582***	0,585***	0,484***	0,576***	0,519***	0,575***
	(0,013)	(0,012)	(0,025)	(0,022)	(0,018)	(0,018)
Constante	0,504*	0,692**	0,045	-0,083	0,055	0,374
	(0,296)	(0,307)	(0,511)	(0,479)	(0,429)	(0,457)
Observaciones	16.031	16.028	19.672	19.681	27.646	27.640
	Tests de variables instrumentales
Test de endogeneidad de Wooldridge (1995)	1,579	2,791	0,118	0,409	0,008	0,515
Test de instrumentos débiles de Stock y Yogo (2005)	19,055***	19,060***	8,263***	7,888***	7,128***	7,062***

Notas: Errores estándar entre paréntesis y clusterizados a nivel de distrito. Una missing flag ha sido incluida para evitar información perdida en años de experiencia del/la tutor/a, estatus socioeconómico y competencias estandarizadas. La hipótesis nula del test de endogeneidad de Wooldridge (1995) es que la variable endógena es ahora exógena y la hipótesis nula del test de instrumentos débiles de Stock y Yogo (2005) es que el instrumento es débil.

Método estimación: Regresión discontinua difusa (regresión discontinua y mínimos cuadrados en dos etapas). El instrumento del tamaño de clase es el tamaño de clase que los colegios deberían haber fijado si hubieran seguido la legislación educativa.

Variable dependiente: Calificaciones estandarizadas usando la media y desviación típica de la población.

Coeficiente: *** Significativo al 1%, ** significativo al 5%, * significativo al 10%.

Fuente: Elaboración propia.

5. Discusión y conclusiones

En este trabajo se ha analizado la cuestión del tamaño de la clase y su relación con el rendimiento académico de los estudiantes de educación primaria y secundaria para el caso español. Para ello, hemos aprovechado los datos del censo de la región española de Andalucía, mediante el uso de un enfoque de regresión discontinua difusa. Esta metodología ha sido empleada debido a las decisiones tomadas por los/as directores/as para la asignación de los estudiantes a las clases, que no siguieron estrictamente la ley española de tamaño de clase, lo que nos ha impedido utilizar directamente un enfoque de regresión discontinua nítida.

En este contexto, nuestros resultados indican que el tamaño de la clase no parece ser una variable relevante en la determinación del rendimiento académico de los estudiantes en educación primaria y secundaria, teniendo un mayor peso las características de los estudiantes que componen la clase, como resaltaron previamente autores como como Akerhielm (1995), Köhler (2020) – quien también indicó que otras características como las de los docentes o la funcionalidad escolar pueden ser relevantes – o Li y Konstantopoulos (2017) – quienes destacaron que la dinámica, instrucción y prácticas del aula pueden ser relevantes también. Así, nuestros resultados están en consonancia con los encontrados por autores como Whitmore (2014) o Zyngier (2014), quienes remarcaron que el tamaño de la clase no es tan relevante en los grados superiores; sin embargo, en nuestro caso, parece que no es tan relevante ni siquiera en los inferiores, como encuentran autores como Angrist et al. (2019), Lovaina y Løkken (2017) y Li y Konstantopoulos (2017). Estos resultados han pasado varios contrastes que indican que nuestro instrumento de tamaño de clase ha funcionado con éxito.

Esto es relevante en términos de legislaciones educativas y decisiones presupuestarias para España. En este sentido, la percepción común (sin sustento empírico) de que un mayor tamaño de clase es negativo para el rendimiento académico de los estudiantes puede suponer el desencadenamiento de políticas educativas dirigidas a reducir el tamaño de las clases, lo que puede aumentar el número de clases por centro y, por tanto, incrementar los gastos aparejados a contratar más docentes para estas clases (Filges et al., 2018). Sin embargo, nuestros resultados apoyan que un tamaño de clase más grande podría no ser un problema, teniendo una mayor relevancia las habilidades de los estudiantes que asisten a la clase. Por ejemplo, esto puede indicar que una clase grande formada por estudiantes con grandes competencias podría no ser un problema, pero una clase pequeña de estudiantes con pocas competencias podría serlo. Debido a esto, parece que las recientes políticas de tamaño de clase aplicadas en España, que tenían como objetivo mejorar el rendimiento académico de los estudiantes, resultaron poco útiles tanto en la educación primaria como en la secundaria y pueden ser el origen de gastos innecesarios, concluyendo que las decisiones de política educativa deben basarse en evidencia empírica para cada caso particular, más que en la intuición.

Además, la pandemia de COVID-19 que vivimos hoy en día puede tener un impacto sobre esta cuestión (Oikawa, Tanaka, Bessho, y Noguchi, 2020; Phillips, Browne, Anand, y Bauch, 2021), ya que el tamaño de clase se ha vuelto incluso más restrictivo, por lo que se debe desarrollar una evidencia clara y sólida sobre este tema antes de la pandemia, para que las consecuencias de esta situación se puedan evaluar adecuadamente.

Este trabajo no está libre de limitaciones: a pesar de presentar una alta validez interna para Andalucía, no tiene tanta validez externa, ya que las decisiones sobre el tamaño de las clases pueden variar según el país (como encuentran autores como Blatchford, 2016, y Shen y Konstantopoulos, 2019) o incluso por región dentro de España. Además, nuestros resultados solo son aplicables a estudiantes de educación primaria y secundaria en los cursos académicos analizados.

Los trabajos de investigación futuros podrían estar dirigidos a analizar esta cuestión del tamaño de la clase con esta misma metodología para el resto de regiones españolas cuando se disponga de datos censales para ellas, y también para el conjunto de España, a efectos de comparación internacional, o incluso para otros países. Además, estudiar la educación infantil o grados superiores, como los estudios de bachillerato o universitarios, puede resultar interesante para futuras investigaciones. Finalmente, analizar las consecuencias sobre este tema del tamaño de la clase en tiempos de COVID-19 también podría ser interesante para futuros trabajos de investigación.

Referencias bibliográficas

Akerhielm, K. (1995). Does class size matter? Economics of Education Review, 14(3), 229–241. doi: 10.1016/0272-7757(95)00004-4

Anghel, B., y Cabrales, A. (2014). The Determinants of success in Primary Education in Spain. Revista de Evaluación de Programas y Políticas Públicas, 2, 22–53. doi: 10.5944/reppp.2.2014.12030

Angrist, J. D., y Lavy, V. (1999). Using Maimonides’ rule to estimate the effect of class size on scholastic achievement. The Quarterly Journal of Economics, 114(2), 533–575.

Angrist, J. D., Lavy, V., Leder-Luis, J., y Shany, A. (2019). Maimonides Rule Redux. American Economic Review: Insights, 1(3), 309–324. doi: 10.1257/aeri.20180120

Argaw, B. A., y Puhani, P. A. (2018). Does class size matter for school tracking outcomes after elementary school? Quasi-experimental evidence using administrative panel data from Germany. Economics of Education Review, 65, 48–57. doi: 10.1016/j.econedurev.2018.06.005

Barua, R., y Lang, K. (2016). School Entry, Educational Attainment and Quarter of Birth: A Cautionary Tale of a Local Average Treatment Effect. Journal of Human Capital, 10(3), 347–376. doi: 10.1086/687599

Blatchford, P. (2016). Is it true that class size does not matter? A critical review of research on class size effects. En P. Blatchford, K. Wing, M. Galton, K.-C. Lai, y J. Chi-Kin (Eds.), Class Size: Eastern and Western perspectives (pp. 92–104). New York: Routledge.

BOE (2006). Organic Law 2/2006, 3rd May, of Education (LOE). Spain: Nº 106, 4th May 2006, 17158–17207.

Bowne, J. B., Magnuson, K. A., Schindler, H. S., Duncan, G. J., y Yoshikawa, H. (2017). A Meta-Analysis of Class Sizes and Ratios in Early Childhood Education Programs: Are Thresholds of Quality Associated With Greater Impacts on Cognitive, Achievement, and Socioemotional Outcomes? Educational Evaluation and Policy Analysis, 39(3), 407–428. doi: 10.3102/0162373716689489

Breton, T. R. (2014). Evidence that class size matters in 4th grade mathematics: An analysis of TIMSS 2007 data for Colombia. International Journal of Educational Development, 34, 51–57. doi: 10.1016/j.ijedudev.2013.04.003

Chingos, M. M., y Whitehurst, G. J. (2011). Class Size: What Research Says and What It Means for State Policy. Washington D.C: Brookings Institution.

Dhuey, E., Figlio, D., Karbownik, K., y Roth, J. (2019). School Starting Age and Cognitive Development. Journal of Policy Analysis and Management, 38(9), 538–578. doi: 10.1002/pam.22135

Dolton, P., y Marcenaro-Gutierrez, O. D. (2011). If you pay peanuts do you get monkeys? A cross-country analysis of teacher pay and pupil performance. Economic Policy, 26(65), 5–55. doi: 10.1111/j.1468-0327.2010.00257.x

Ehrenberg, R. G., Brewer, D. J., Gamoran, A., y Willms, J. D. (2001). Class Size and Student Achievement. Psychological Science in the Public Interest, 2(1), 1–30. doi: 10.1111/1529-1006.003

Etim, J. S., Etim, A. S., y Blizard, Z. D. (2020). Class Size and School Performance: An Analysis of Elementary and Middle Schools. International Journal on Studies in Education, 2(2), 66–77. doi: 10.46328/ijonse.13

Feir, D., Lemieux, T., y Marmer, V. (2016). Weak Identification in Fuzzy Regression Discontinuity Designs. Journal of Business & Economic Statistics, 34(2), 185–196. doi: 10.1080/07350015.2015.1024836

Filges, T., Sonne-Schmidt, C. S., y Nielsen, B. C. V. (2018). Small class sizes for improving student achievement in primary and secondary schools: a systematic review. Campbell Systematic Reviews, 14(1), 1–107. doi: 10.4073/csr.2018.10

Finn, J. D., y Achilles, C. M. (1999). Tennessee’s Class Size Study: Findings, Implications, Misconceptions. Educational Evaluation and Policy Analysis, 21(2), 97–109. doi: 10.3102/01623737021002097

Finn, J. D., Pannozzo, G. M., y Achilles, C. M. (2003). The “Why’s” of Class Size: Student Behavior in Small Classes. Review of Educational Research, 73(3), 321–368. doi: 10.3102/00346543073003321

Fiorini, M., y Stevens, K. (2014). Assessing the Monoticity Assumption in IV and fuzzy RD designs. The University of Sydney Economics Working Paper Series, 13, 1–52.

Francis, J., y Barnett, W. S. (2019). Relating preschool class size to classroom quality and student achievement. Early Childhood Research Quarterly, 49, 49–58. doi: 10.1016/j.ecresq.2019.05.002

García-Pérez, J. I., Hidalgo-Hidalgo, M., y Robles-Zurita, J. A. (2014). Does grade retention affect students’ achievement? Some evidence from Spain. Applied Economics, 46(12), 1373–1392. doi: 10.1080/00036846.2013.872761

Goldstein, H., Yang, M., Omar, R., Turner, R., y Thompson, S. (2000). Meta-analysis using multilevel models with an application to the study of class size effects. Journal of the Royal Statistical Society: Series C (Applied Statistics), 49(3), 399–412. doi: 10.1111/1467-9876.00200

Hanushek, E. A. (2002). Evidence, politics, and the class size debate. En L. Mishel, y R. Rothstein (Eds.), The class size debate (pp. 37–65). Washington, DC: Economic Policy Institute.

Hanushek, E. A. (2011). The economic value of higher teacher quality. Economics of Education Review, 30(3), 466–479. doi: 10.1016/j.econedurev.2010.12.006

Jepsen, C., y Rivkin, S. (2009). Class Size Reduction and Student Achievement. Journal of Human Resources, 44(1), 223–250. doi: 10.3368/jhr.44.1.223

Köhler, T. (2020). Class size and learner outcomes in South African schools: The role of school socioeconomic status. Development Southern Africa, in press. doi: 10.1080/0376835x.2020.1845614

Krueger, A. B. (2003). Economic Considerations and Class Size. The Economic Journal, 113(485), F34–F63. doi: 10.1111/1468-0297.00098

Leuven, E., y Løkken, S. A. (2017). Long Term Impacts of Class Size in Compulsory School. IZA Discussion Papers No. 10594, 1–36.

Li, W., y Konstantopoulos, S. (2017). Does class-size reduction close the achievement gap? Evidence from TIMSS 2011. School Effectiveness and School Improvement, 28(2), 292–313. doi: 10.1080/09243453.2017.1280062

MECD (2018). Panorama de la educación Indicadores de la OCDE 2018. Informes Español. Madrid: Instituto Nacional de Evaluación Educativa.

MECD (2019). PISA 2018. Programa para la Evaluación Internacional de los Estudiantes. Informe español. Madrid: Ministerio de Educación y Formación Profesional.

MECD (2020). PISA 2018. Programa para la Evaluación Internacional de los Estudiantes. Resultados de lectura en España. Madrid: Ministerio de Educación y Formación Profesional.

Mora, T., Escardíbul, J.-O., y Espasa, M. (2010). The effects of regional educational policies on school failure in Spain. Revista de Economía Aplicada Número, 54(18), 79–106. http://www.redalyc.org/articulo.oa?id=96915832004

Mosteller, F. (1995). The Tennessee Study of Class Size in the Early School Grades. The Future of Children, 5(2), 113–127. doi: 10.2307/1602360

OECD (2012). How Does Class Size Vary Around the World? Paris: OECD Library.

OECD (2016). PISA 2015 Results (Volume I): Excellence and Equity in Education. Paris: PISA, OECD Publishing. doi: 10.1787/9789264266490-en

Oikawa, M., Tanaka, R., Bessho, S.-I., y Noguchi, H. (2020). Do Class Size Reductions Protect Students from Infectious Disease? Lessons for Covid-19 Policy from Flu Epidemic in Tokyo Metropolitan Area. IZA Discussion Paper No. 13432, 1–30.

Phillips, B., Browne, D. T., Anand, M., y Bauch, C. T. (2021). Model-based projections for COVID-19 outbreak size and student-days lost to closure in Ontario childcare centres and primary schools. Scientific Reports, 11, 6402. doi: 10.1038/s41598-021-85302-6

Shen, T., y Konstantopoulos, S. (2019). Estimating causal effects of class size in secondary education: evidence from TIMSS. Research Papers in Education, in press. doi: 10.1080/02671522.2019.1697733

Shin, I.-S., y Young, J. (2009). Class size and student achievement in the United States: A meta-analysis. KEDI Journal of Educational Policy, 6(2), 3–19.

Stock, J. H., y Yogo, M. (2005). Testing for weak instruments in linear IV regression. En D. W. K. Andrews, y J. H. Stock (Eds.), Identification and Inference for Econometric Models: Essays in Honor of Thomas Rothenberg (pp. 80–108). New York: Cambridge University Press.

Uttl, B., Bell, S., y Banks, K. (2018). Student Evaluation of Teaching (SET) Ratings Depend on the Class Size: A Systematic Review. Proceedings of International Academic Conferences 8110392, International Institute of Social and Economic Sciences.

Whitmore, D. (2014). Does Class size Matter? Colorado Boulder: National Education Policy Center.

Wößmann, L., y West, M. (2006). Class-size effects in school systems around the world: Evidence from between-grade variation in TIMSS. European Economic Review, 50(3), 695–736. doi: 10.1016/j.euroecorev.2004.11.005

Wooldridge, J. M. (1995). Score diagnostics for linear models estimated by two stage least squares. En G. S. Maddala, T. N. Srinivasan, y P. C. B. Phillips (Eds.), Advances in Econometrics and Quantitative Economics: Essays in Honor of Profesor C. R. Rao (pp. 66–87). Oxford: Blackwell.

Zyngier, D. (2014). Class size and academic results, with a focus on children from culturally, linguistically and economically disenfranchised communities. Evidence Base, 1, 1–24. doi: 10.21307/eb-2014-001

Información de contacto: Luis Alejandro López-Agudo, Universidad de Málaga, Facultad de Ciencias Económicas y Empresariales, Departamento de Economía Aplicada (Estadística y Econometría). Plaza de El Ejido s/n, 29013, Málaga (España). E-mail: lopezagudo@uma.es

Anexo

TABLA A1. Estadísticos descriptivos y test de diferencias de medias entre la población y la muestra empleada

		Cuarto grado. 2012-13						Octavo grado. 2012/13						Octavo grado. 2011/12
		Población			Muestra			Población			Muestra			Población			Muestra
Variables		Obs.	Media	D.E.	Obs.	Media	D.E.	Obs.	Media	D.E.	Obs.	Media	D.E.	Obs.	Media	D.E.	Obs.	Media	D.E.
Sexo del estudiante	Varón	90.048	0,51	0,50	16.433	0,52	0,50	86.626	0,52	0,50	19.880	0,52	0,50	88.271	0,52	0,50	28.109	0,52	0,50
	Mujer	90.048	0,49	0,50	16.433	0,48	0,50	86.626	0,48	0,50	19.880	0,48	0,50	88.271	0,48	0,50	28.109	0,48	0,50
Nivel educativo del padre	Primaria incompleta o no asistió al colegio	70.745	0,13	0,33	12.822	0,13	0,33	62.998	0,15D	0,36	13.916	0,16D	0,36	61.706	0,16D	0,36	19.638	0,15D	0,35
	EGB o Educación Secundaria Obligatoria	70.745	0,34D	0,47	12.822	0,35D	0,48	62.998	0,35D	0,48	13.916	0,38D	0,48	61.706	0,35D	0,48	19.638	0,33D	0,47
	Bachillerato, Formación Profesional de Primer Grado, Escuela de Arte Elemental y Profesiones Artísticas, BUP, COU, Escuela Oficial de Idiomas o Ciclo Formativo de Grado Medio	70.745	0,21	0,41	12.822	0,21	0,41	62.998	0,21	0,40	13.916	0,21	0,41	61.706	0,21	0,41	19.638	0,21	0,41
	Formación Profesional de Segundo Grado, Especialidad en Arte y Profesiones Artísticas o Ciclo Formativo de Grado Superior	70.745	0,12D	0,33	12.822	0,11D	0,31	62.998	0,10	0,31	13.916	0,10	0,31	61.706	0,10	0,31	19.638	0,11	0,31
	Grado Universitario, Doctorado	70.745	0,20	0,40	12.822	0,20	0,40	62.998	0,19D	0,39	13.916	0,15D	0,36	61.706	0,18D	0,38	19.638	0,20D	0,40
Nivel educativo de la madre	Primaria incompleta o no asistió al colegio	79.641	0,09	0,29	14.447	0,09	0,29	70.425	0,12D	0,33	15.651	0,13D	0,34	68.675	0,13D	0,34	21.758	0,12D	0,32
	EGB o Educación Secundaria Obligatoria	79.641	0,35	0,48	14.447	0,35	0,48	70.425	0,38D	0,49	15.651	0,41D	0,49	68.675	0,39D	0,49	21.758	0,37D	0,48
	Bachillerato, Formación Profesional de Primer Grado, Escuela de Arte Elemental y Profesiones Artísticas, BUP, COU, Escuela Oficial de Idiomas o Ciclo Formativo de Grado Medio	79.641	0,21	0,41	14.447	0,21	0,41	70.425	0,21	0,41	15.651	0,21	0,41	68.675	0,21	0,41	21.758	0,21	0,41
	Formación Profesional de Segundo Grado, Especialidad en Arte y Profesiones Artísticas o Ciclo Formativo de Grado Superior	79.641	0,12D	0,33	14.447	0,12D	0,32	70.425	0,10D	0,30	15.651	0,09D	0,29	68.675	0,09	0,29	21.758	0,10	0,30
	Grado Universitario, Doctorado	79.641	0,23	0,42	14.447	0,23	0,42	70.425	0,19D	0,39	15.651	0,16D	0,37	68.675	0,18D	0,38	21.758	0,20D	0,40
Ocupación del padre	Dirección de empresas o administración pública	70.349	0,07	0,26	12.715	0,07	0,26	62.302	0,08D	0,27	13.778	0,07D	0,25	61.434	0,07D	0,26	19.594	0,08 D	0,27
	Técnicos/as, profesionales, científicos/as e intelectuales. Armada (oficiales y altos rangos)	70.349	0,13	0,34	12.715	0,13	0,34	62.302	0,13D	0,33	13.778	0,11D	0,30	61.434	0,13D	0,34	19.594	0,14D	0,36
	Técnicos/as de apoyo y profesionales. Empleados/as administrativos. Pequeños/as empresarios/as	70.349	0,21	0,40	12.715	0,20	0,40	62.302	0,20D	0,40	13.778	0,19D	0,40	61.434	0,20D	0,40	19.594	0,21D	0,41
	Trabajadores/as de hotel, personal, protección y vendedores/as. Armada (sub-oficiales y bajos rangos)	70.349	0,14D	0,35	12.715	0,13D	0,34	62.302	0,13	0,34	13.778	0,14	0,35	61.434	0,14	0,35	19.594	0,14	0,35
	Trabajadores/as de agricultura y pesca. Artesanos/as y trabajadores/as manufactureros cualificados/as, de construcción y de mina	70.349	0,34D	0,47	12.715	0,35D	0,48	62.302	0,33D	0,47	13.778	0,36D	0,48	61.434	0,33D	0,47	19.594	0,30D	0,46
	Trabajadores/as no cualificados/as	70.349	0,05D	0,22	12.715	0,06D	0,23	62.302	0,06D	0,23	13.778	0,06D	0,24	61.434	0,06	0,23	19.594	0,06	0,23
	Dedicado/a a las labores domésticas del hogar	70.349	0,01	0,10	12.715	0,01	0,10	62.302	0,01	0,10	13.778	0,01	0,11	61.434	0,01	0,10	19.594	0,01	0,09
	Inactivo/a	70.349	0,05	0,23	12.715	0,05	0,22	62.302	0,06	0,24	13.778	0,06	0,25	61.434	0,06	0,23	19.594	0,06	0,23
Ocupación de la madre	Dirección de empresas o administración pública	78.575	0,03	0,18	14.231	0,03	0,18	69.282	0,04	0,19	15.358	0,03	0,18	67.804	0,03D	0,17	21.513	0,03D	0,18
	Técnicos/as, profesionales, científicos/as e intelectuales. Armada (oficiales y altos rangos)	78.575	0,13	0,34	14.231	0,13	0,34	69.282	0,12D	0,32	15.358	0,10D	0,30	67.804	0,12D	0,32	21.513	0,13D	0,34
	Técnicos/as de apoyo y profesionales. Empleados/as administrativos. Pequeños/as empresarios/as	78.575	0,18	0,38	14.231	0,18	0,38	69.282	0,15D	0,37	15.358	0,15D	0,36	67.804	0,16D	0,36	21.513	0,17D	0,37
	Trabajadores/as de hotel, personal, protección y vendedores/as. Armada (sub-oficiales y bajos rangos)	78.575	0,13D	0,34	14.231	0,12D	0,33	69.282	0,12D	0,33	15.358	0,13D	0,33	67.804	0,13	0,34	21.513	0,13	0,34
	Trabajadores/as de agricultura y pesca. Artesanos/as y trabajadores/as manufactureros cualificados/as, de construcción y de mina	78.575	0,07D	0,25	14.231	0,07D	0,26	69.282	0,07D	0,26	15.358	0,08D	0,27	67.804	0,06D	0,23	21.513	0,06D	0,22
	Trabajadores/as no cualificados/as	78.575	0,09	0,28	14.231	0,09	0,28	69.282	0,10D	0,29	15.358	0,10D	0,30	67.804	0,10D	0,32	21.513	0,10D	0,31
	Dedicado/a a las labores domésticas del hogar	78.575	0,34	0,47	14.231	0,35	0,48	69.282	0,37D	0,48	15.358	0,38D	0,49	67.804	0,37D	0,48	21.513	0,35D	0,48
	Inactivo/a	78.575	0,03	0,17	14.231	0,03	0,17	69.282	0,03	0,17	15.358	0,03	0,17	67.804	0,03	0,17	21.513	0,03	0,17
Número de libros en el hogar	Entre 0 y 100	82.465	0,67	0,47	14.948	0,67	0,47	73.075	0,63D	0,48	16.262	0,65D	0,48	71.284	0,65D	0,48	22.625	0,63D	0,48
	Entre 101 y 200	82.465	0,16	0,37	14.948	0,16	0,36	73.075	0,17	0,37	16.262	0,17	0,37	71.284	0,17D	0,37	22.625	0,17D	0,38
	Más de 200	82.465	0,17	0,38	14.948	0,17	0,38	73.075	0,20D	0,40	16.262	0,18D	0,39	71.284	0,18D	0,39	22.625	0,20D	0,40
Recursos del hogar	Lugar para estudiar	82.527	0,95	0,22	14.956	0,95	0,22	73.093	0,96	0,19	16.284	0,96	0,20	71.342	0,96D	0,19	22.647	0,97D	0,18
	Internet	82.186	0,83D	0,38	14.899	0,82D	0,39	73.045	0,89D	0,31	16.262	0,88D	0,32	71.036	0,89D	0,31	22.538	0,90D	0,30
	Libros (novelas, cuentos, poemas, cómics…)	82.319	0,96	0,19	14.904	0,96	0,19	72.888	0,96D	0,21	16.207	0,95D	0,22	70.796	0,94D	0,25	22.479	0,94D	0,23
Financiación del colegio	Público	90.048	0,76D	0,42	16.433	0,70D	0,46	86.626	0,74D	0,44	19.880	0,91D	0,29	88.271	0,75D	0,43	28.109	0,66D	0,47
	Concertado	90.048	0,21D	0,41	16.433	0,25D	0,44	86.626	0,24D	0,43	19.880	0,08D	0,27	88.271	0,23D	0,42	28.109	0,31D	0,46
	Privado	90.048	0,03D	0,16	16.433	0,05D	0,22	86.626	0,02D	0,13	19.880	0,01D	0,10	88.271	0,02D	0,15	28.109	0,03D	0,16

Notas: “Obs.” significa “Observaciones” y “D.E.” significa “Desviación estándar”. La “D” indica que hay diferencias significativas (significativas al 5% o menos) entre las columnas de media de la “Población” y de media de la “Muestra” dentro de cada grado y curso académico.

Fuente: Elaboración propia.

---