La repetición perjudica la inclusión social en la escuela
Repetition undermines social inclusion at school
https://doi.org/10.4438/1988-592X-RE-2025-409-685
Pablo Brañas-Garza
Universidad Loyola Andalucía
https://orcid.org/0000-0001-8456-6009
Diego Jorrat
Universidad Loyola Andalucía
Resumen
Independientemente de otros posibles efectos, la repetición de curso obliga a los estudiantes a desconectar de sus amigos de la clase y a conectar con sus nuevos compañeros de clase. Este trabajo cuantifica como la repetición tiene implicaciones en la integración social de los estudiantes. Para mirar los efectos de corto plazo, empleamos el método de emparejamiento por puntuaciones de propensión para comparar al repetidor con un “gemelo estadístico”. Para el largo plazo, comparamos repetidores actuales con otros que lo hicieron anteriormente. Los resultados no son optimistas. En el corto plazo, los repetidores son menos populares, tiene mayor número de enemigos y menos “buenos” amigos dentro de la clase. Además, aparecen con mayor frecuencia en las redes de odio. En el largo plazo, los repetidores “antiguos” son algo más populares que los actuales, pero en todo lo demás son iguales. Podemos concluir que la repetición tiene un impacto muy negativo en las relaciones sociales de los estudiantes y que dicho efecto apenas se aminora con el paso del tiempo.
Palabras clave:
Adolescentes, redes sociales, repetición de curso, vulnerabilidad escolar, inclusión social, comportamiento social, sistema educativo
Abstract
Regardless of other possible effects, grade retention forces students to disconnect from their friends in class and connect with their new classmates. This study quantifies how grade retention affects students´ social integration. To analyse short-term effects, we use a propensity score matching to compare retained students with their “statistical twins”. For long-term effects, we compare current repeaters with those who repeated in the past. The results are not optimistic. In the short term, retained students are less popular, have more enemies and fewer "good" friends in the classroom. They are also more likely to appear in hate networks. In the long term, ´former´ retained students are slightly more popular than current students, but in all other respects they remain the same. We conclude that grade retention has a strong negative impact on students´ social relationships, and that this effect hardly diminishes over time.
Keywords:
Adolescents, social networks, grade retention, school vulnerability, social inclusion, social behaviour, education systemIntroducción
Uno de los problemas más graves del sistema educativo español es el alto número de repeticiones. Según el informe Panorama de la Educación 2024, España presenta una tasa de repetición del 7.8% en la primera etapa de educación secundaria y del 6.5% en la segunda, mientras que el promedio para los países de la OECD es menos de la mitad de esos números (2.2% y 3.2% respectivamente). La repetición escolar implica que un estudiante que ha cursado un año académico completo permanezca en ese mismo nivel un año académico adicional. Es importante destacar que la decisión sobre la repetición raramente proviene del entorno del estudiante, sino que es adoptada colegiadamente por el equipo docente del centro educativo. Según el Real Decreto 984/2021, la repetición es una medida excepcional y solo se permite un máximo de dos veces a lo largo de la etapa, siempre basada en la evaluación del progreso del alumno y su capacidad para alcanzar los aprendizajes esenciales.
Según las estadísticas publicadas en el Anuario estadístico del Ministerio de Educación, Formación Profesional y Deportes (MEFPD, 2024), con datos del curso 2022-2023, en Enseñanza Secundaria Obligatoria (ESO) repitió el 7,3% de los estudiantes de primero, el 6,8% de los de segundo, el 7,3% de los de tercero y el 6,7% de los de cuarto. Además, el porcentaje de hombres supera siempre y en todos los cursos al de las mujeres. Especialmente llamativo resulta el porcentaje de varones que repiten en el primer curso de la ESO que llega hasta el 8,7% (vs. 5,8% de las mujeres).
Si bien los números de repetidores son elevados, la realidad es que hay muchos argumentos para dudar que dicha política tenga algún tipo de beneficio. Por un lado, parece que permanecer un año más en el mismo curso tiene efectos cuando menos inciertos en el desempeño académico. Podríamos pensar que la retención puede tener beneficios al mejorar el aprendizaje – asentar conocimientos – y permitir una mejor alineación entre los conocimientos del estudiante y el nivel de enseñanza. Sin embargo, la evidencia sugiere que esto no ocurre y que incluso reduce el rendimiento escolar (García Pérez et al., 2014).
En segundo lugar, estos potenciales beneficios parecen venir acompañado de altos costes personales para el estudiante: la estigmatización por parte de docentes o de los mismos compañeros, disminución en la confianza en sí mismo y dificultades para adaptarse a un nuevo grupo de estudio (véase Manacorda, 2012). De hecho, hay evidencia causal de que la repetición escolar afecta positivamente a la probabilidad de abandono escolar (Jacob y Lefgren, 2009; Manacorda, 2012; De Witte et al., 2013; Freeman y Simonsen, 2015; González-Rodríguez et al., 2019).
En tercer y último lugar, la repetición de curso supone un alto coste financiero para las instituciones puesto que deben de financiar un año adicional para el estudiante que repite. Y este año que repite también tiene un coste económico para el estudiante: su inserción laboral de los estudiantes también se retrasa, lo que implica a su vez un retraso en la obtención de ingresos laborales (Tafreschi y Thiemann, 2016).
El estudio del problema de la repetición se ha centrado casi exclusivamente en cuestiones meramente académicas como el rendimiento educativo de los repetidores o los factores asociados a una mayor probabilidad de repetición (ver por ejemplo González-Rodríguez et al.,2016; González-Betancor et al., 2019; López et al., 2023 y Nieto-Isidro et al., 2023). Parece bastante sorprendente que se haya hecho poco esfuerzo en estudiar como la repetición impacta en la integración social de los estudiantes. Al fin y al cabo, a un estudiante que al que se le hace repetir se le separa de sus amigos de clase y además se le obliga a interaccionar con nuevos compañeros. Esto no parece que vaya a resultar a coste cero.
En este trabajo vamos a estudiar precisamente este problema: el coste
de repetir en la integración social de los estudiantes. Cuando hablamos
de integración social nos referimos al número de amigos, a la
popularidad, la centralidad y al
Además, TeensLab dispone de las medidas (individuales) de redes referidas con anterioridad y, lo que es más importante, la base de datos contiene información de más de 200 redes de clase independientes. Como veremos posteriormente, las medidas de redes son cálculos computacionales que no tienen ninguna dimensión subjetiva, sino que simplemente cuentan (dan un valor numérico) a cada una de las variables de interés. Dicho de otro modo, el análisis de redes no nos dice si el estudiante se siente más o menos solo sino si efectivamente está más solo – independientemente de que lo sienta o incluso que lo sepa.
Este trabajo busca responder a dos preguntas de investigación. En primer lugar, queremos medir el efecto de la repetición en la integración social del estudiante. En segundo lugar, si este efecto dura en el tiempo o se desvanece a los pocos años.
Para lo primero comparamos las medidas de redes entre repetidores y no repetidores. Para evitar problemas obvios de endogeneidad – los repetidores son distintos de los no repetidores porque de hecho están repitiendo – usamos una técnica estadística llamada “emparejamiento por puntuaciones de propensión” (PSM en adelante) que nos permite buscar dentro de la base de datos TeensLab a gemelos idénticos de los repetidores, es decir, estudiantes que son estadísticamente similares en determinadas características a los repetidores salvo en esto último. El emparejamiento se realiza basándose en variables tanto observables como inobservables para los docentes (como paciencia, aversión al riesgo y habilidades cognitivas), todas ellas medidas en TeensLab. Este método nos permite aislar el efecto “causal” de repetir en las variables de resultados puesto que compara muestras que son comparables. Es importante además destacar que al comparar repetidores con sus compañeros de clase estamos midiendo el efecto inmediato (o de corto plazo) de repetir.
Para lo segundo, analizamos a estudiantes que están repitiendo con otros que no lo están haciendo pero que lo hicieron en el pasado. Dicho de otro modo, los dos comparten el estigma de haber repetido sólo que unos lo sufren ahora y otros lo sufrieron en el pasado. Como veremos a lo largo del trabajo estos dos grupos presentan características observables e inobservables similares, por lo que se puede suponer que ambos grupos son análogos y que cualquier diferencia en las medidas de integración social son atribuibles al efecto de repetir actualmente de curso. Este segundo análisis nos permite medir si los efectos perduran o no en el tiempo.
Método
Integración Social y Métricas De Redes
El estudio de las relaciones entre los estudiantes dentro de la clase no es un tema nuevo. Los sociogramas se comenzaron a usar en la década de los 30 en los EEUU y desde entonces se han usado de manera generalizada, sobre todo, para identificar patrones de interacción, detectar conflictos y mejorar la convivencia dentro del aula. Como veremos a lo largo de esta sección la métrica unidireccional (la que hace referencia a que un sujeto llame a otro) es relativamente sencilla. Sin embargo, la métrica que recoge las interacciones entre sujetos – por ejemplo, el camino más corto (o más largo) entre dos sujetos – puede ser muy engorrosa. Al lector interesado se le recomienda el libro de Jackson (2010) y la colección de trabajos editado por Bramoullé et al. (2016). También puede consultar el trabajo de Ruiz-García et al. (2023) sobre la creación de índice sobre relaciones triádicas, es decir, como tercer amigo de una pareja de amigos se hace amigo del otro.
Lo anterior implica que habrá compañeros de clase que sean “extraños”
para el sujeto
Pensamos en una clase pequeña con solo seis estudiantes y donde cada
uno de los seis tiene su conjunto de amigos.
FIGURA I. Ejemplo de red con 6 estudiantes
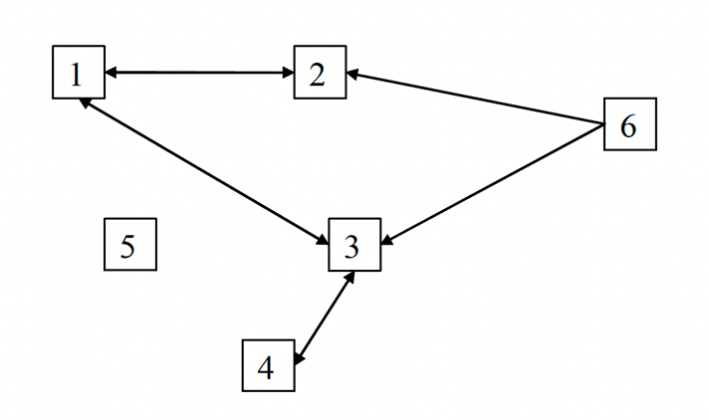
Fuente: Elaboración propia.
La Figura I nos pone de manifiesto un fenómeno común en las redes.
Los estudiantes 1 y 2 se nombraron mutuamente -
Cuando miramos redes como las de TeensLab encontramos que muchas de
las relaciones no son recíprocas, sino que están declaradas por sólo uno
de los dos. Dicho de otro modo,
En la literatura de redes
FIGURA II. Ejemplo de jugador central
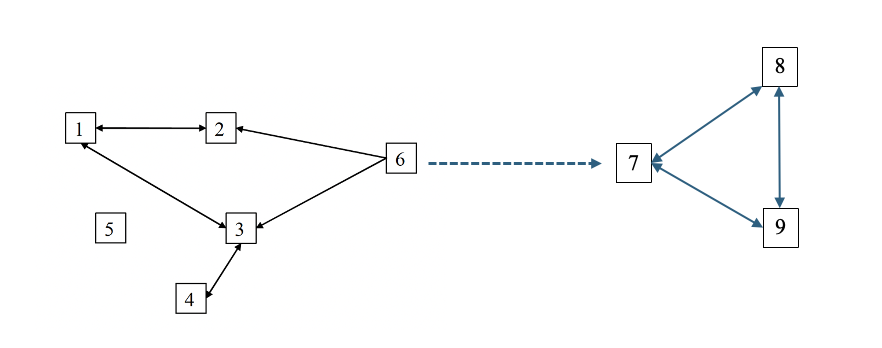
Fuente: Elaboración propia usando datos del TeensLab.
Desafortunadamente no existe una única definición de centralidad,
sino que por el contrario hay muchas – centralidad, autovalor, rango,
etc. Nosotros usaremos una métrica muy común:
La Base de Datos TeensLab
El TeensLab es un consorcio entre las universidades de Barcelona, Carlos III, Granada, Loyola y País Vasco que tiene como objetivo estudiar el comportamiento económico en adolescentes de España. Existe evidencia que muestra que estas habilidades (cognitivas y no cognitivas) son determinantes importantes de la toma de decisiones en la vida real de los adultos, y además se correlacionan con variables asociadas con los “buenos resultados” como la educación, el ahorro, etc. (ver Dohmen et al., 2011; Golsteyn et al., 2014; Falk et al., 2018; Angerer et al., 2023).
El proyecto Teenslab recopila datos de un total de 5.890 estudiantes de 33 centros educativos de dos regiones de España, Andalucía y Cataluña. Los datos se recogieron con el acuerdo de los directores de los centros, siguiendo estrictas normas de anonimato y confidencialidad. Para ello se combinaron métodos de encuestas y experimentos de laboratorio en el campo. Las principales dimensiones medidas en este conjunto de datos incluyen: i) preferencias económicas (por el riesgo y el tiempo), ii) habilidades cognitivas, iii) pensamiento estratégico, y iv) métricas sobre redes a nivel de la clase. Además, se incluyen variables que recogen diferentes factores sociodemográficos del estudiante, y una serie de variables complementarias que recogen datos sobre el aspecto físico, el estado de ánimo (felicidad) y las expectativas, entre otras.
El diseño de este experimento presenta ciertas particularidades.
Primero, se incluyó como una actividad en clase en cada centro para
incrementar la tasa de respuesta (ver Alfonso et al., 2023) y se realizó
por medio de una plataforma online llamada SAND (Social Analysis and
Network Data) para garantizar la protección de
datos
Tercero, el cuestionario se administró íntegramente en español y debido a políticas restrictivas en las escuelas, se utilizaron incentivos hipotéticos (y no reales) en las tareas experimentales. Sin embargo, se ha documentado que el comportamiento de adolescentes y adultos no difiere entre esquemas de pago reales e hipotéticos, al menos para las preferencias de riesgo y tiempo, lo que sugiere la fiabilidad de los resultados (Brañas-Garza et al., 2021 y 2023; Alfonso et al., 2023).
Por último, los datos comprenden estudiantes entre los 10 y los 23 años (Media=14,10, SD=1,94), es decir que pertenecen a diversos niveles educativos como la enseñanza primaria (8.62%), secundaria (84.94%), bachillerato (1.90%) y algunos de formación profesional (4.53%). La muestra se encuentra balanceada por genero (49.68% son mujeres, 49.68% hombres y el restante 0.64% corresponde a la categoría “otro” o “prefiero no responder”).
Los datos completos están disponibles para ser usados por cualquier
investigador en un repositorio
En este trabajo se utilizan datos de 1821 estudiantes. Este número es menor al de base de datos TeensLab por dos motivos. Primero, nos concentramos solo en estudiantes de la Educación Secundaria Obligatoria (ESO), lo que nos deja una muestra de 5003 estudiantes. Segundo, la pregunta sobre si repite o repitió algún curso se agregó sólo en 11 centros escolares, quedando una muestra de 2155 estudiantes de la ESO con los que se cuenta información sobre esta variable. Como se verá a continuación usaremos finalmente 1,821 observaciones porque se eliminaron 129 sujetos que había repetido hace más de un año y 205 sujetos porque tenían datos faltantes en algunas de las variables. A continuación, se presenta la estrategia empírica y los datos que se utilizarán en este artículo.
Variables utilizadas, estrategia empírica y método de estimación
Para responder a las preguntas de este trabajo y dar cierta evidencia causal, es necesario aplicar diferentes estrategias empíricas. Se entiende como problema de endogeneidad cuando una variable explicativa está correlacionada con el término de error en un modelo de regresión. Esto conduce a estimaciones sesgadas e inconsistentes del efecto causal de la repetición en las variables de resultados.
El problema de la endogeneidad puede surgir por varias razones pero
en nuestro caso destacamos dos:
Vamos a realizar dos análisis distintos. En primer lugar, vamos a
comparar repetidores con no repetidores pero que tienen un perfil
similar. Para ello usaremos metodología estadística llamada
emparejamiento por puntuaciones de propensión (PSM) con un enfoque de
emparejado de
Antes de entrar en detalle en la estrategia empírica describiremos
las variables que se utilizan en este estudio. En
La razón por las que usamos paciencia y la tolerancia al riesgo como controles es porque nos permiten capturar “inobservables”. Por ejemplo, hay mucha evidencia de que la paciencia está asociada a la perseverancia y suele estar correlacionada con los buenos resultados académicos (ver Brañas-Garza et al. 2019b para una revisión). La tolerancia al riesgo está asociada con actividades muy diversas, desde el emprendimiento al consumo de alcohol (ver Dohmen et al. 2011 para una revisión).
La Tabla I presenta un resumen de las variables. Cabe destacar, que las variables de desempeño académico, paciencia y tolerancia al riesgo fueron estandarizadas utilizando el método min-max, transformándolas en un rango de 0 a 1, donde valores más altos indican mayor nivel en cada característica.
TABLA I. variables utilizadas para emparejar y variables de resultado
| N | Mean | SD | Min | Max | |
|---|---|---|---|---|---|
| Repetidor | 1821 | 0.04 | 0.20 | 0 | 1 |
| Mujer | 1821 | 0.49 | 0.50 | 0 | 1 |
| CRT | 1821 | 0.50 | 0.27 | 0 | 1 |
| Desempeño | 1821 | 0.63 | 0.40 | 0 | 1 |
| Paciencia | 1821 | 0.48 | 0.35 | 0 | 1 |
| Riesgo | 1821 | 0.60 | 0.16 | 0 | 1 |
| Edad | 1821 | 14.24 | 1.14 | 10 | 18 |
| Migrante | 1821 | 0.21 | 0.41 | 0 | 1 |
| In-degree amigos | 1821 | 8.12 | 3.85 | 0 | 21 |
| In-degree mejores amigos | 1821 | 2.93 | 2.01 | 0 | 11 |
| In-degree enemigos | 1821 | 2.34 | 2.50 | 0 | 22 |
| In-degree peores enemigos | 1821 | 0.70 | 1.27 | 0 | 12 |
| Out-degree amigos | 1821 | 9.00 | 6.30 | 0 | 30 |
| Out-degree mejores amigos | 1821 | 3.20 | 2.90 | 0 | 28 |
| Out-degree enemigos | 1821 | 2.80 | 3.61 | 0 | 29 |
| Out-degree peores enemigos | 1821 | 0.82 | 1.63 | 0 | 29 |
| Betweenness amigos | 1821 | 16.86 | 19.22 | 0 | 63.73 |
| Betweenness mejores amigos | 1821 | 16.35 | 24.67 | 0 | 80.14 |
| Betweenness enemigos | 1821 | 10.55 | 18.68 | 0 | 62.67 |
| Betweenness peores enemigos | 1821 | 0.76 | 2.11 | 0 | 8 |
| Clustering amigos | 1821 | 0.68 | 0.19 | 0 | 1 |
| Clustering mejores amigos | 1821 | 0.52 | 0.34 | 0 | 1 |
| Clustering enemigos | 1821 | 0.23 | 0.29 | 0 | 1 |
| Clustering peores enemigos | 1821 | 0.06 | 0.19 | 0 | 1 |
Fuente: Elaboración propia usando datos del TeensLab.
Adicionalmente, en la parte baja de la Tabla I se muestran también
las variables de resultado que vamos a usar para medir la integración
social. Analizamos cuatro dimensiones.
A continuación, procederemos a explicar cuál es la estrategia empírica que seguiremos para medir el efecto de corto y largo plazo de repetir.
Comparación entre los que están repitiendo y no repetidores
El principal desafío al comparar repetidores y no repetidores es que estos grupos pueden diferir en aspectos como el rendimiento académico, la paciencia, el riesgo y en otras características. Si no controlamos estas diferencias, cualquier comparación directa podría llevar a conclusiones incorrectas, ya que los efectos observados en la integración social podrían deberse a otros factores y no necesariamente a la repetición. Para resolver este problema, el PSM estima la probabilidad de que un estudiante repita curso (puntuación) basándose en una serie de características individuales. Luego, cada repetidor se empareja con estudiantes no repetidores que tienen una puntuación similar, asegurando así que ambos grupos sean comparables.
Para estimar la puntuación, se utilizan las variables descritas en la parte superior de la Tabla I. Adicionalmente, aplicamos “emparejamiento perfecto” en las variables migrante, CRT, edad y nota media (o GPA). Esto garantiza que cada repetidor solo se compare con no repetidores que coinciden exactamente en estas características clave.
Existen diferentes formas de realizar el emparejamiento. Un método
común es asignar a cada repetidor un solo estudiante no repetidor con la
puntuación más cercana (emparejamiento 1 a 1). Sin embargo, este enfoque
puede ser ineficiente, ya que desperdicia información y puede generar
estimaciones más inestables. En cambio, utilizamos el método de
emparejamiento
Para evaluar si el emparejamiento ha generado un grupo de comparación adecuado, realizamos tres pruebas claves:
- 1 -
Diferencias en medias antes y después del emparejamiento (Figura III, panel izquierdo). Antes del emparejamiento, los repetidores y no repetidores presentan diferencias significativas en varias características. Estas diferencias se representan con los círculos y se refieren a los datos brutos. Sin embargo, después del emparejamiento, estas diferencias desaparecen o se reducen en los datos emparejados representadas por los triángulos, lo que indica que los grupos se han balanceado correctamente.
FIGURA III. Diferencia de medias y ratio de varianza: Repetidores vs. No Repetidores.
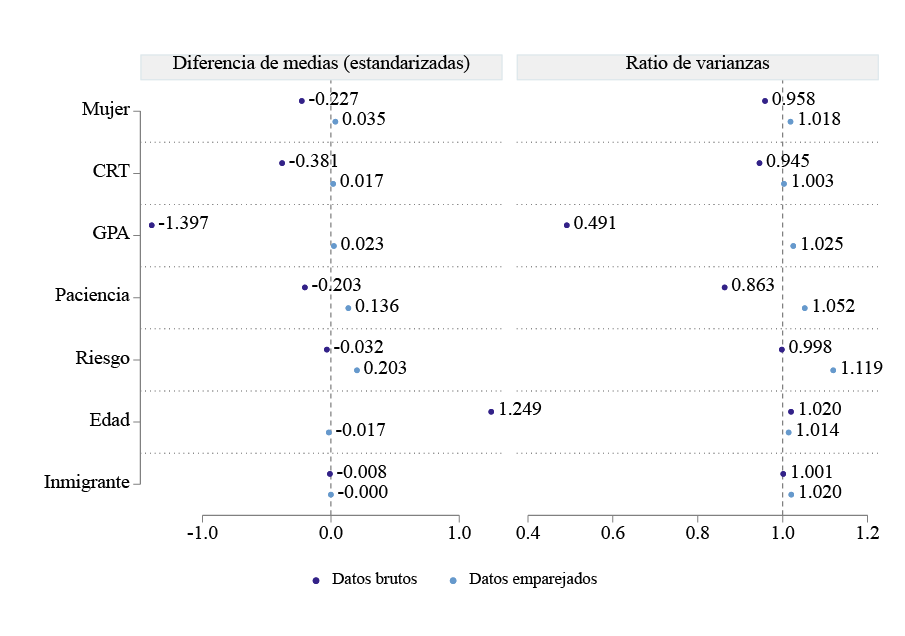
Fuente: Elaboración propia de acuerdo con datos del TeensLab.
- 2 -
Ratio de varianza entre repetidores y no repetidores (Figura III, panel derecho). Un buen emparejamiento no solo equilibra las medias, sino que también iguala la dispersión de los datos. El panel derecho de la Figura III muestra que, antes del emparejamiento, la varianza de las características en ambos grupos era diferente (círculos), pero después del emparejamiento, la mayoría de los valores se acercan a 1 (triángulos), lo que sugiere que ambos grupos tienen distribuciones similares. - 3 -
Distribución de la puntuación de emparejamiento antes y después del emparejamiento (Figura IV). El panel de arriba muestra la distribución de la puntuación (de emparejamiento) mientras que el panel de abajo muestra la distribución acumulada de esta variable. Ambos paneles, muestran cómo, antes del emparejamiento (panel izquierdo o “Datos brutos”), las distribuciones de repetidores y no repetidores eran bastante diferentes. Después del emparejamiento (panel derecho o “Datos emparejados”), las distribuciones son mucho más similares, lo que indica un soporte común adecuado. Esto significa que hay suficientes estudiantes no repetidores con características comparables a los repetidores, lo que permite una comparación válida.
FIGURA IV. Distribución (arriba) y distribución acumulada (abajo) de la puntuación de emparejamiento.
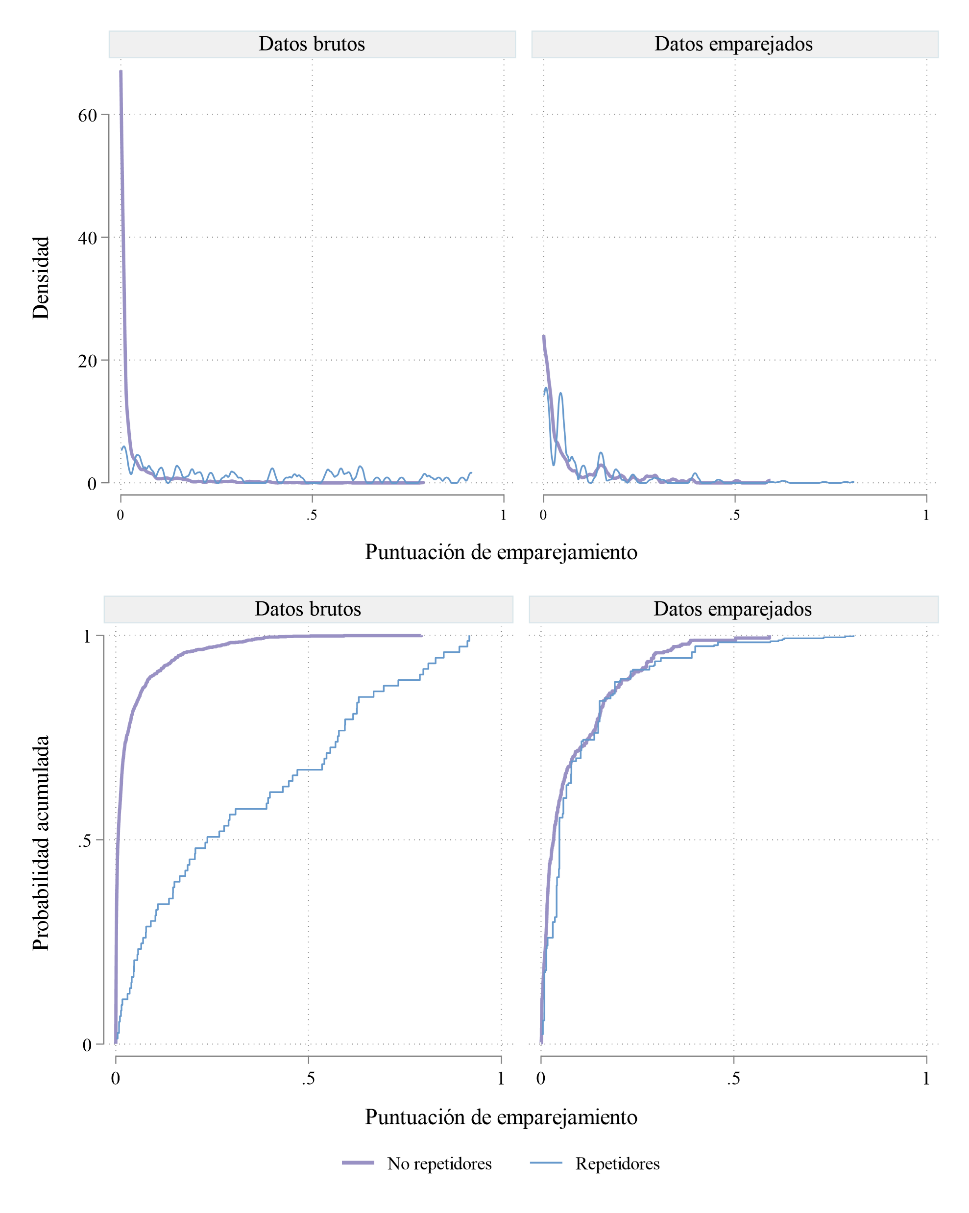
Fuente: Elaboración propia usando datos del TeensLab.
Dado que las pruebas muestran un buen balance de las variables clave, una varianza equilibrada y un soporte común adecuado, se puede concluir que el emparejamiento realizado con Kernel PSM ha funcionado correctamente. Esto nos permite estimar con mayor precisión el efecto de la repetición en la integración social, comparando a los repetidores con un grupo de no repetidores bien definido.
Para estimar el efecto, simplemente compararemos la media de cada variable de resultado para el grupo de repetidores con la media para los no repetidores ponderada por la puntuación. Cabe destacar que este análisis nos permite estimar el efecto promedio del tratamiento sobre los tratados (ATT, es decir, el impacto de la repetición en los estudiantes que efectivamente han repetido y no el efecto del tratamiento promedio (ATE, que representaría el impacto de la repetición si se aplicara a todos los estudiantes. Por tanto, el efecto inmediato estimado de repetir en cada variable de resultado es:
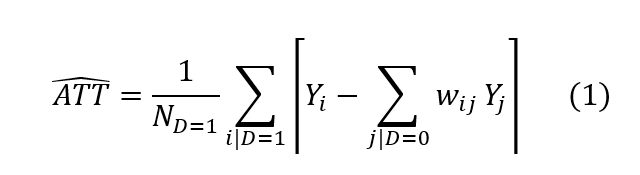
donde
Por último, aunque el KPSM reduce significativamente el sesgo de selección, no garantiza una identificación causal perfecta, ya que podrían existir factores inobservables que influyen tanto en la repetición como en la integración social (por ejemplo, la motivación personal o el apoyo familiar). Aun así, dentro de los métodos observacionales, el KPSM representa una estrategia sólida para generar una comparación válida entre repetidores y no repetidores.
Comparación entre los que están repitiendo y los que repitieron anteriormente
Para estimar si la repetición tiene un efecto duradero en el tiempo, usaremos la muestra de repetidores, pero a diferencia del apartado anterior no los compararemos con gemelos artificiales sino con otros sujetos que repitieron el curso anterior o hace más tiempo. Como se aprecia en la Tabla II, se utilizan 203 sujetos que son repetidores, de los cuales 74 están repitiendo en el momento que se hizo el experimento, y 129 que repitieron algún curso anterior. Asimismo, se puede apreciar que no existen diferencias significativas en cuánto a género, GPA, CRT, paciencia, riesgo y edad; como así también en ser inmigrante o haber repetido más de un curso.
TABLA II. Diferencias en variables observables: Repetidores actuales vs. previos.
| Repite | Diferencia | |||
|---|---|---|---|---|
| ≥1 año | Ahora | |||
| (1) | (2) | (2) – (1) | ||
| Mujer | 0.442 | 0.378 | -0.063 | |
| (0.499) | (0.488) | (0.072) | ||
| CRT | 0.360 | 0.405 | 0.045 | |
| (0.262) | (0.266) | (0.039) | ||
| GPA | 0.311 | 0.180 | -0.131*** | |
| (0.354) | (0.273) | (0.048) | ||
| Paciencia | 0.483 | 0.414 | -0.068 | |
| (0.334) | (0.321) | (0.048) | ||
| Riesgo | 0.618 | 0.592 | -0.026 | |
| (0.178) | (0.164) | (0.025) | ||
| Edad | 15.411 | 15.575 | 0.164 | |
| (1.275) | (1.117) | (0.180) | ||
| Migrante | 0.198 | 0.216 | 0.018 | |
| (0.400) | (0.414) | (0.059) | ||
| Múltiples repeticiones | 0.132 | 0.162 | 0.030 | |
| (0.340) | (0.371) | (0.051) | ||
| Observaciones | 129 | 74 | 203 | |
Fuente: elaboración propia con datos del TeensLab. Nota: Errores estándares en paréntesis. La columna
diferencia nos permite testar la igualdad de medias. ***p<0.01; **p<0.05 y *p<0.10.
La única diferencia significativa (
En resumen, las dos submuestras son comparables en casi todas las
variables observables, por lo que podemos asumir que también son
similares en las variables inobservables. Bajo este supuesto de
identificación, podemos estimar el efecto duradero de repetir utilizando
un modelo de regresión lineal múltiple. Para ello se estima el siguiente
modelo por Mínimo Cuadrados Ordinarios para cada variable de resultado
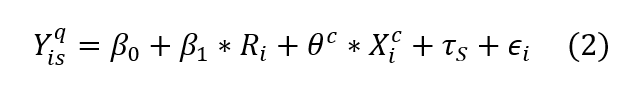
Donde
Resultados
Siguiendo el esquema del trabajo dividimos los resultados en dos secciones. En primer lugar, comparamos los que repiten ahora con otros que no están repitiendo y que comparten características comunes, es decir, un “gemelo”. En segundo lugar, los comparamos con otros estudiantes que repitieron en el pasado. Cabe destacar, que todo el análisis se realizó con Stata 18.
Comparación entre los que están repitiendo y no repetidores
En esta sección comparamos a los estudiantes que repiten ahora con el
resto de la clase que no son repetidores. La Figura V muestra las
estimaciones del
Del panel A encontramos que los repetidores son menos populares
(
Los repetidores no llaman ni más ni menos amigos que el reto de sus
compañeros (panel B) sin embargo llaman a un menor número de mejores
amigos (
En el
De todo lo anterior resumimos:
Resultado 1: Los repetidores son menos populares, tiene mayor número de enemigos y tienen menos “buenos” amigos en la clase. Además, aparecen con mayor frecuencia en las redes de odio y tienen enemigos que son amigos entre sí.
Estos resultados son relevantes porque el grupo con el que comparamos
a los repetidores es un gemelo, es decir, idéntico en todas las
características excepto en el hecho de que es repetidor. Si bien el
método KPSM no puede dar evidencia
Dado un conjunto de estudiantes muy similares, algunos de ellos, por mala suerte, fueron seleccionados para repetir mientras que otros tuvieron la fortuna de no hacerlo. Asumiendo que este proceso fue meramente estocástico podemos decir que la repetición hace que los estudiantes destruyan su capital social, dicho de otro modo, su integración social se ve seriamente dañada.
FIGURA V. Efecto promedio del tratamiento (repetir) sobre los tratados (ATT) basándose en KPSM y sus intervalos de confianza al 95%. Se consideran en la estimación efectos fijos por colegio.
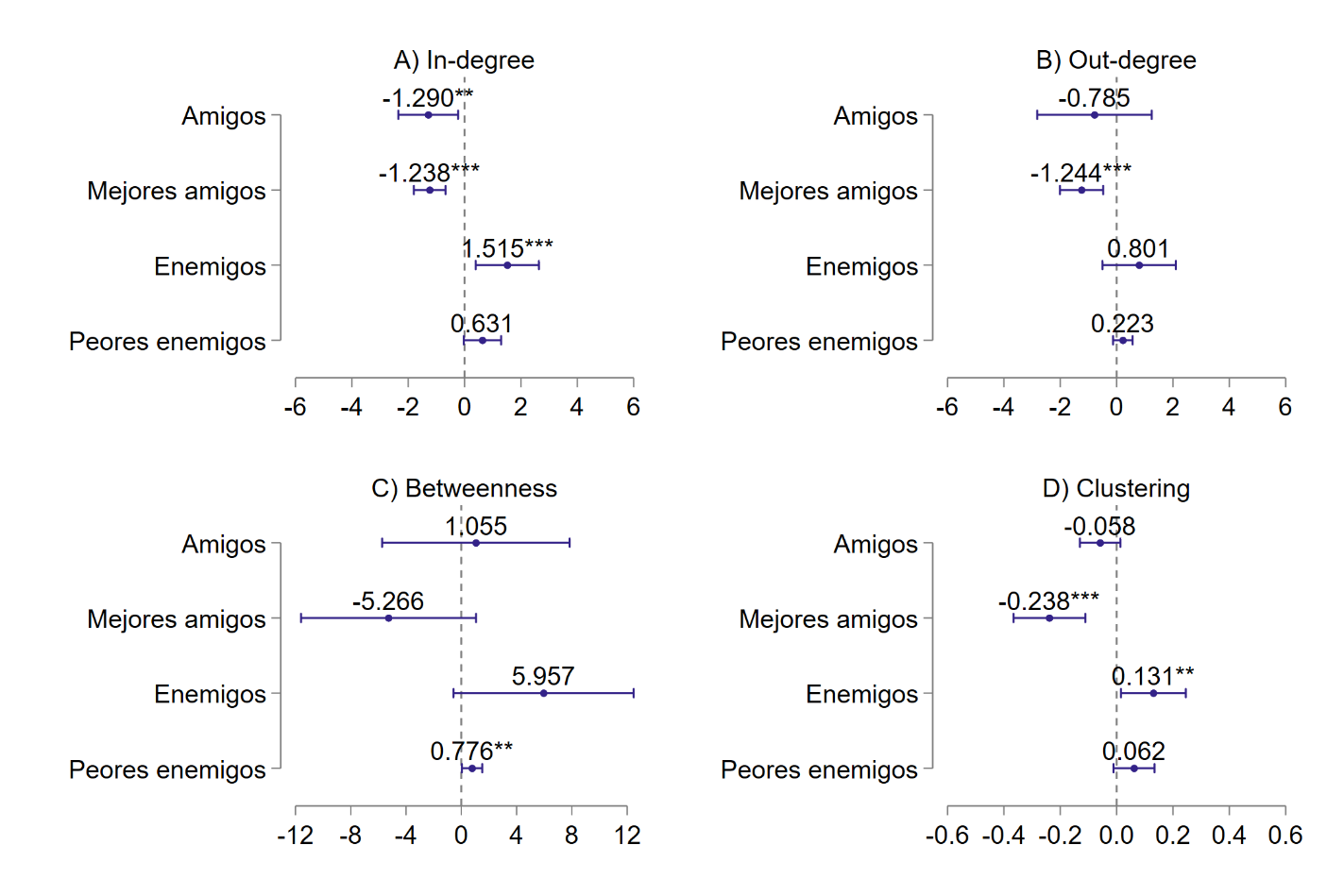
Fuente: elaboración propia con datos del TeensLab.
Comparación entre los que están repitiendo y los que repitieron anteriormente
En el apartado anterior hemos visto que la repetición tiene un impacto negativo en la integración social, pero no sabemos cuánto dura este impacto, dicho de otro modo, si los estudiantes recuperan su capital social un curso o varios cursos después. Para responder a esta pregunta vamos a estudiar las diferencias entre estudiantes que están repitiendo y estudiantes que repitieron algún curso anterior, pero la medida de inclusión social se refiere al momento en que se realiza cada experimento. Es decir, todos los sujetos en este análisis tienen el estigma de ser repetidores sólo que algunos de ellos lo sufren ahora mientras que otros lo sufrieron antes.
La Figura VI muestra los coeficientes estimados
Tampoco encontramos ningún tipo de efecto en el out-degree (panel B). Los estudiantes que repiten ahora no llaman a más o menos amigos (enemigos) que los que repitieron anteriormente. Tampoco vemos diferencias substanciales respecto a centralidad (panel C) ni ningún tipo de impacto en el clustering (panel D). Para una mejor descripción de los resultados, en las Tablas A2 a A5 del Anexo C, se presentan las estimaciones de las regresiones, tanto con controles como sin controles para cada variable de resultado.
De manera resumida:
Resultado 2: Comparados con otros estudiantes que repitieron en el pasado, los repetidores del curso actual son menos populares en la red de amigos. No hay diferencias significativas en
out-degree , centralidad ni en clustering.
Si bien no podemos y no debemos hacer conclusiones muy definitivas de
una muestra tan pequeña (
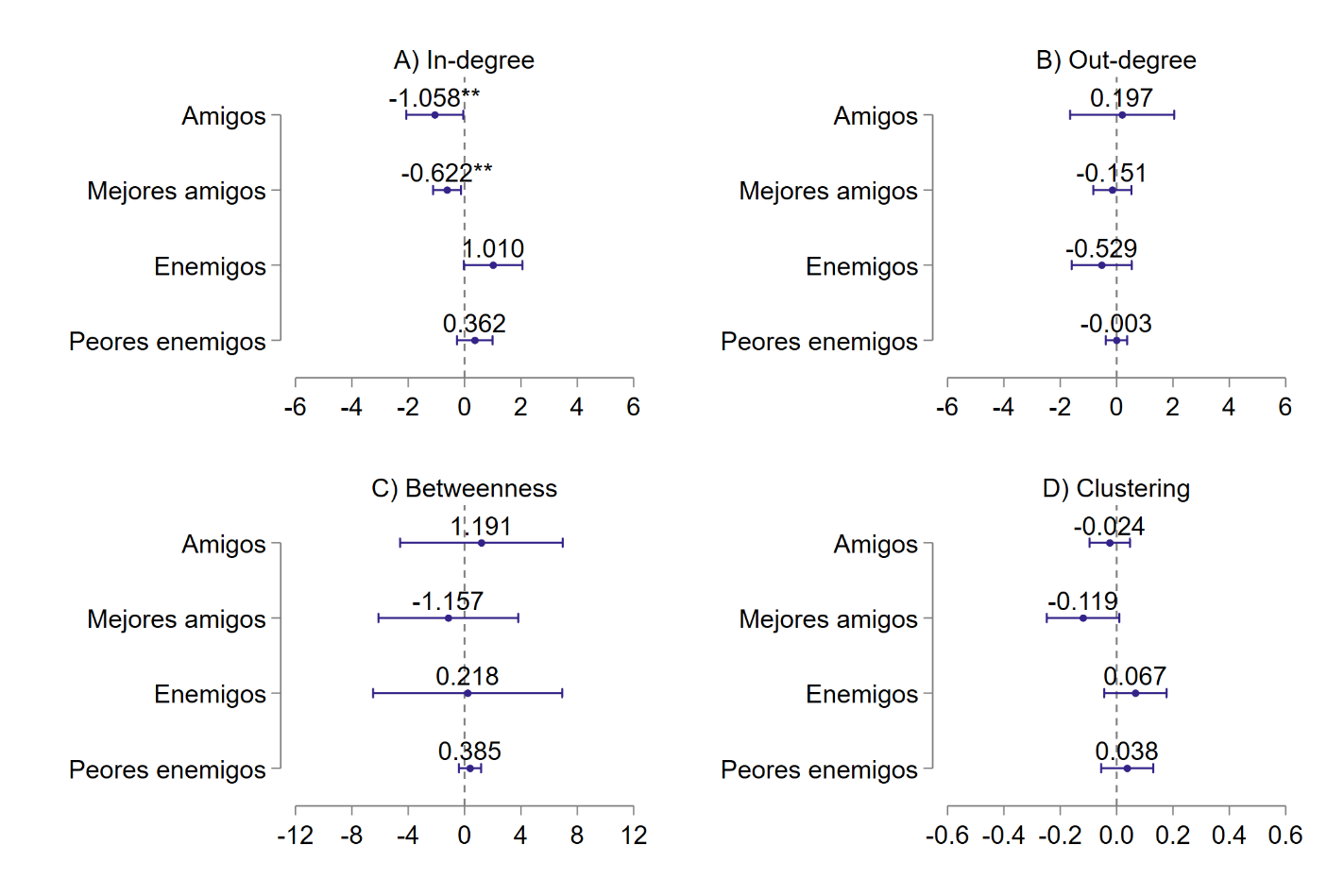 FIGURA
VI. Efectos estimados sobre repetidores actuales y anteriores,
basándose en el modelo de regresión lineal múltiple y sus intervalos de
confianza del 95%. Se consideran efectos fijos por colegio.
FIGURA
VI. Efectos estimados sobre repetidores actuales y anteriores,
basándose en el modelo de regresión lineal múltiple y sus intervalos de
confianza del 95%. Se consideran efectos fijos por colegio.
Fuente: elaboración propia con datos del TeensLab.
Esto quiere decir que, a excepción de la (im)popularidad que parece que disminuye después del año o más de la repetición, todo lo que se mostró en el Resultado 1– mayor número de enemigos y menor de “buenos” amigos, así como mayor presencia en las redes de odio – no cambia con los años. O sea, que los daños de la repetición sobre la integración social de los estudiantes perduran.
Conclusiones
La repetición de estudiantes en España en un problema que viene de lejos y que, si bien ha mejorado levemente, no acaba de resolverse y seguimos mostrando números alarmantes con respecto al resto de países de la OECD.
La investigación existente pone dudas sobre los beneficios reales para el estudiante, puesto que no parece que haya mejoras en el rendimiento escolar (García Pérez et al., 2014) y, sin embargo, sí hay evidencia de costes directos como la estigmatización – por parte de los compañeros e incluso desde los docentes – o la disminución en la confianza en sí mismo (véase Manacorda, 2012). Incluso, hay evidencia causal que indica que la repetición lleva a muchos estudiantes al abandono (Jacob y Lefgren, 2009; Manacorda, 2012; De Witte et al., 2013; Freeman y Simonsen, 2015; González-Rodríguez et al., 2019).
No podemos olvidar, además, que mantener un 10% de repetidores tiene un alto coste para el sistema. Y el coste no es sólo económico, sino que incluso genera problemas logísticos a los centros puesto que deben acomodar más estudiantes en las aulas que, por definición, no son flexibles. Y, además de lo anterior, también impone costes económicos sobre el estudiante que tiene que retrasar su inserción laboral y, por tanto, sufre un retraso en la obtención de ingresos laborales (Tafreschi y Thiemann, 2016).
Este trabajo explora una nueva fuente de problemas para el repetidor. Usando métrica de redes y los datos de TeensLab (Vasco et al. 2025) exploramos cómo impacta la repetición en el capital relacional (integración social) de los estudiantes afectados. El análisis se realiza desde dos enfoques complementarios: en primer lugar, comparamos a los repetidores con compañeros no repetidores que tienen características similares (“gemelos” estadísticos) y, en segundo lugar, con otros repetidores de años anteriores.
Para medir las diferencias en métricas de redes entre repetidores y no repetidores usamos una técnica estadística llamada “emparejamiento por puntuaciones de propensión” que nos permite obtener “gemelos” y, con ello, podemos aislar el efecto “causal” de la repetición en la integración social. Y como estamos comparando repetidores con sus compañeros de clase estamos midiendo el efecto inmediato (o de corto plazo) de repetir. Los resultados son preocupantes. Los repetidores son menos populares, tiene mayor número de enemigos, menos “buenos” amigos, aparecen con mayor frecuencia en las redes de odio y tienen enemigos que son amigos entre sí. En resumen, el efecto de corto plazo de la repetición es devastador en el capital social de los estudiantes, no sólo pierden lazos de amistad, sino que aparecen señalados en redes de odio.
Para ver los efectos de largo plazo, comparamos estudiantes que repitieron en el pasado con los que están repitiendo ahora. Esta comparación tiene mucho sentido porque ambos grupos comparten el estigma de haber repetido. La única diferencia es que unos repiten ahora y otros lo hicieron anteriormente y, por tanto, este análisis nos permite medir qué efectos perduran, es decir, son de largo plazo. Cuando comparamos los repetidores “antiguos” con los actuales encontramos una única diferencia: los nuevos son menos populares. En todas las demás características son idénticos. Por tanto, años después de repetir lo único que logran es mejorar su popularidad y en todo lo demás son iguales. En resumen, tienen menos amigos, más amigos, aparecen centrales en redes de odio, etc. Dicho de otro modo, su capital relacional no se recupera substancialmente más allá de la popularidad.
Por tanto, de este análisis podemos concluir que la repetición afecta muy negativamente al capital social de los estudiantes, les hace perder amigos, ganar enemigos y tomar posiciones relevantes en redes de enemigos. Y además el impacto apenas se aminora con el paso del tiempo.
Agradecimientos y financiación
Queremos dar las gracias al equipo de campo: Pablo Montero, Mónica Vasco, Paula Piña y Emilio Nieto. Esta investigación ha contado con el apoyo del Ministerio de Economía y Competitividad de España (PID2021-126892NB-100), Excelencia-Junta de Andalucía (PY-18-FR-0007) y Agencia Andaluza de Cooperación Internacional para el Desarrollo (AACID-0I008/2020).
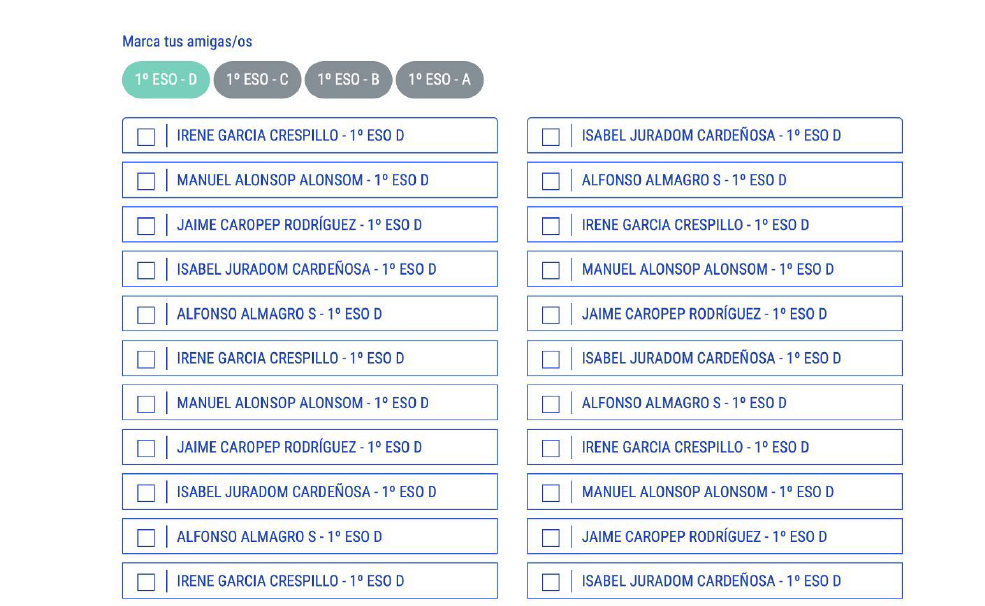
Anexo A: Protocolo de elicitación de redes de TeensLab
Anexo B: Notas autorreportadas, crt, paciencia y riesgo.
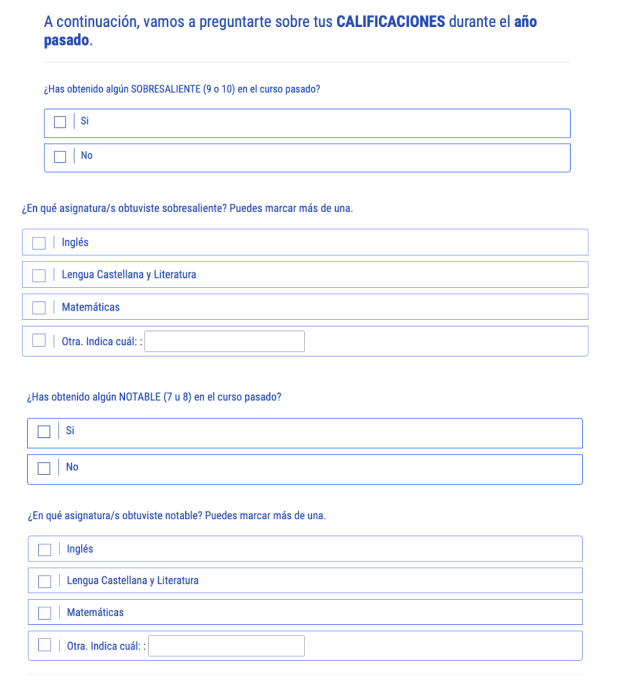
Notas autorreportadas
Para la medición del GPA (nota media), se preguntó a los estudiantes cuántos sobresalientes y notables habían sacado en sus tres asignaturas principales (matemáticas, lengua e inglés) el curso anterior. Un sobresaliente equivale a 2 puntos y un notable a 1 punto, por lo que la variable GPA tiene un máximo de 6 puntos. Para evitar cambios de escala, se procedió a estandarizar esta variable con el método min-max, de tal manera de que varíe entre 0 y 1, donde cualquier valor cercano al 1 significa mayor número de respuestas reflexivas y un mejor desempeño educativo, respectivamente.
Cognitive Reflection Test (CRT)
El CRT hace referencia a la tarea de Reflexión Cognitiva desarrollada por Frederick (2005) y adaptada por Thomson y Oppenheimer (2016) para no adultos. Esta prueba consta de tres preguntas diseñadas para obtener respuestas reflexivas e intuitivas. Cada pregunta presenta una respuesta intuitiva pero incorrecta y una respuesta correcta alcanzable a través de un procesamiento analítico. A partir de esta tarea, se computa el número de respuestas reflexivas, donde puntuaciones más altas indican un mayor razonamiento reflexivo (ver Brañas-Garza et al. 2019b, para una revisión).


Paciencia y Riesgo
Descuento temporal

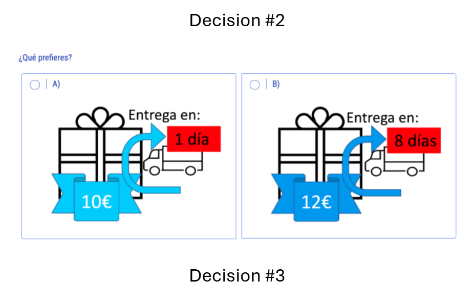
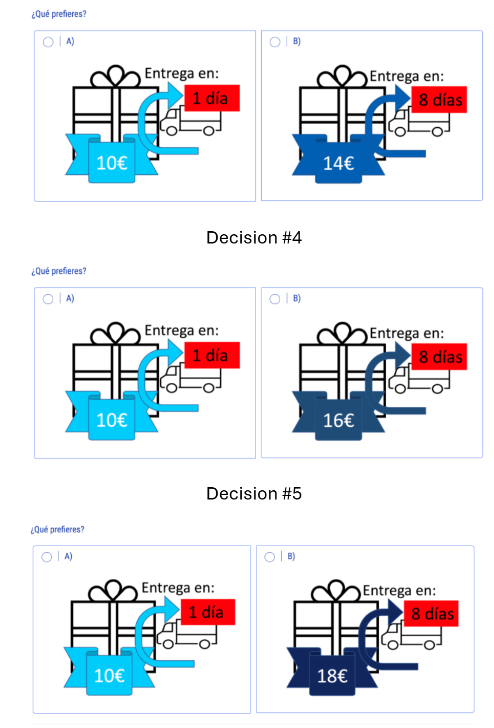

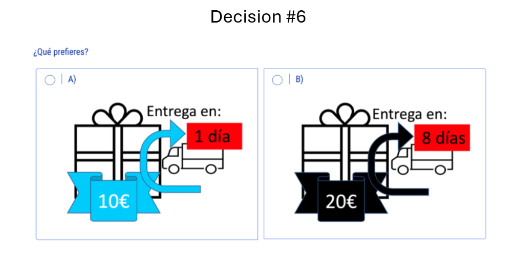
Tolerancia por el riesgo

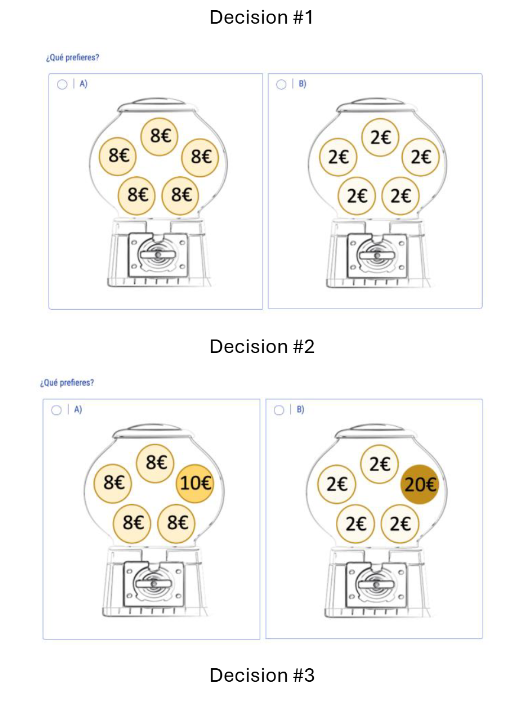
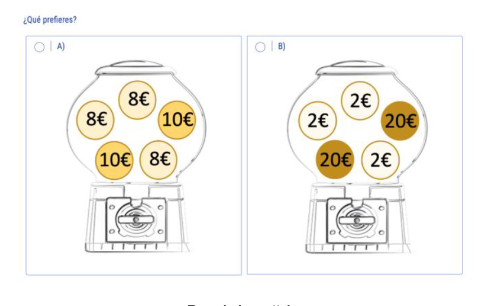
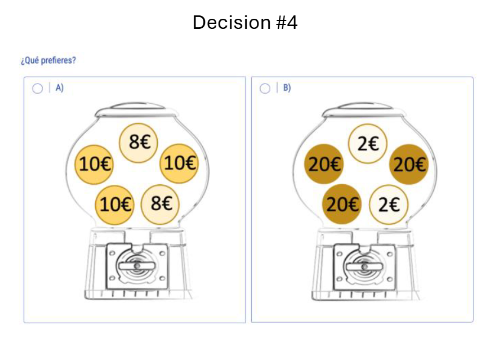

Anexo C: Resultados de las estimaciones
TABLA A1. Estimación del efecto de corto plazo de la repetición. Estimadores ATT utilizando KPSM.
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| Amigos | Mejores Amigos | Enemigos | Peores enemigos | |
| ATT | -1.290** | -1.238*** | 1.515*** | 0.631* |
| (0.540) | (0.287) | (0.572) | (0.339) | |
| Observaciones | 1,821 | 1,821 | 1,821 | 1,821 |
| ATT | -0.785 | -1.244*** | 0.801 | 0.223 |
| (1.036) | (0.392) | (0.664) | (0.177) | |
| Observaciones | 1,821 | 1,821 | 1,821 | 1,821 |
| ATT | 1.055 | -5.266 | 5.957* | 0.776** |
| (3.463) | (3.230) | (3.325) | (0.378) | |
| Observaciones | 1,821 | 1,821 | 1,821 | 1,821 |
| ATT | -0.0584 | -0.238*** | 0.131** | 0.0620* |
| (0.0366) | (0.0650) | (0.0586) | (0.0371) | |
| Observaciones | 1,821 | 1,821 | 1,821 | 1,821 |
| Nota: Errores estándares en paréntesis. Los asteriscos denotan significancia estadística: *** p<0.01, ** p<0.05, * p<0.1 | ||||
TABLA A2. Estimación del efecto duradero de la repetición sobre In-degree, basándose en el análisis de regresión múltiple.
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
|---|---|---|---|---|---|---|---|---|
| Amigos | Amigos | Mejores amigos | Mejores Amigos | Enemigos | Enemigos | Peores enemigos | Peores enemigos | |
| Repetidor | -0.486 | -1.058** | -0.387* | -0.622** | 0.235 | 1.010* | 0.158 | 0.362 |
| (0.495) | (0.511) | (0.234) | (0.252) | (0.565) | (0.528) | (0.316) | (0.319) | |
| Mujer | -0.281 | -0.251 | 0.672 | 0.138 | ||||
| (0.465) | (0.212) | (0.414) | (0.232) | |||||
| CRT | 0.520 | -0.357 | -2.390*** | -1.237*** | ||||
| (0.892) | (0.403) | (0.767) | (0.447) | |||||
| GPA | -0.636 | -0.261 | 0.550 | -0.340 | ||||
| (0.738) | (0.351) | (0.654) | (0.375) | |||||
| Paciencia | -0.915 | -0.722** | 1.428** | 0.720* | ||||
| (0.745) | (0.303) | (0.698) | (0.422) | |||||
| Riesgo | 0.508 | 0.163 | -0.859 | -0.662 | ||||
| (1.463) | (0.693) | (1.075) | (0.567) | |||||
| Edad | 0.035 | 0.110 | -0.541** | -0.341** | ||||
| (0.206) | (0.101) | (0.230) | (0.140) | |||||
| Rep. múltiple cursos | 0.816 | 0.210 | 0.614 | 0.430 | ||||
| (0.669) | (0.289) | (0.780) | (0.517) | |||||
| Constante | 7.629*** | 7.665** | 2.396*** | 1.319 | 2.322*** | 10.257*** | 0.947** | 6.571*** |
| (0.740) | (3.419) | (0.363) | (1.674) | (0.593) | (3.840) | (0.460) | (2.264) | |
| Observaciones | 203 | 190 | 203 | 190 | 203 | 190 | 203 | 190 |
| 0.161 | 0.222 | 0.135 | 0.199 | 0.118 | 0.222 | 0.047 | 0.124 | |
| EF escuela | Sí | Sí | Sí | Sí | Sí | Sí | Sí | Sí |
| Controles | No | Sí | No | Sí | No | Sí | No | Sí |
| Nota: Errores estándares en paréntesis. Los asteriscos denotan significancia estadística: *** p<0.01, ** p<0.05, * p<0.1 | ||||||||
TABLA A3. Estimación del efecto duradero de la repetición sobre Out-degree, basándose en el análisis de regresión múltiple.
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
|---|---|---|---|---|---|---|---|---|
| Amigos | Amigos | Mejores amigos | Mejores Amigos | Enemigos | Enemigos | Peores enemigos | Peores enemigos | |
| Repetidor | -0.200 | 0.197 | -0.352 | -0.151 | -0.394 | -0.529 | -0.080 | -0.003 |
| (0.946) | (0.936) | (0.395) | (0.343) | (0.484) | (0.540) | (0.202) | (0.192) | |
| Mujer | -1.761** | -0.123 | 1.124** | 0.094 | ||||
| (0.822) | (0.305) | (0.544) | (0.247) | |||||
| CRT | -1.279 | 0.091 | 2.023* | 0.423 | ||||
| (1.656) | (0.533) | (1.164) | (0.488) | |||||
| GPA | 1.916 | -0.375 | 1.466 | 0.763 | ||||
| (1.260) | (0.471) | (0.974) | (0.538) | |||||
| Paciencia | 0.168 | -0.151 | -0.267 | 0.199 | ||||
| (1.101) | (0.424) | (0.689) | (0.307) | |||||
| Riesgo | -2.033 | -0.746 | -1.596 | 0.542 | ||||
| (2.394) | (0.828) | (1.267) | (0.515) | |||||
| Edad | 0.453 | 0.206 | -0.372 | -0.036 | ||||
| (0.428) | (0.152) | (0.247) | (0.138) | |||||
| Rep. múltiple cursos | 0.484 | -0.086 | 1.721** | 0.228 | ||||
| (1.477) | (0.410) | (0.683) | (0.224) | |||||
| Constante | 6.267*** | 0.718 | 2.584*** | -0.026 | 2.731* | 7.977* | 0.827*** | 0.514 |
| (1.554) | (6.722) | (0.606) | (2.482) | (1.470) | (4.573) | (0.234) | (2.089) | |
| Observaciones | 203 | 190 | 203 | 190 | 203 | 190 | 203 | 190 |
| 0.081 | 0.111 | 0.073 | 0.049 | 0.057 | 0.139 | 0.028 | 0.035 | |
| EF escuela | Sí | Sí | Sí | Sí | Sí | Sí | Sí | Sí |
| Controles | No | Sí | No | Sí | No | Sí | No | Sí |
| Nota: Errores estándares en paréntesis. Los asteriscos denotan significancia estadística: *** p<0.01, ** p<0.05, * p<0.1 | ||||||||
TABLA A4. Estimación del efecto duradero de la repetición sobre Betweenness, basándose en el análisis de regresión múltiple.
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
|---|---|---|---|---|---|---|---|---|
| Amigos | Amigos | Mejores amigos | Mejores Amigos | Enemigos | Enemigos | Peores enemigos | Peores enemigos | |
| Repetidor | 1.678 | 1.191 | -1.410 | -1.157 | -1.312 | 0.218 | 0.093 | 0.385 |
| (2.922) | (2.922) | (2.313) | (2.513) | (3.053) | (3.400) | (0.390) | (0.397) | |
| Mujer | -4.719* | 2.810 | 7.355** | 0.916** | ||||
| (2.519) | (2.433) | (3.034) | (0.353) | |||||
| CRT | -2.674 | -8.275 | 0.267 | -0.887 | ||||
| (4.412) | (5.199) | (5.407) | (0.660) | |||||
| GPA | 4.414 | -5.443** | 5.298 | 0.160 | ||||
| (4.111) | (2.557) | (5.560) | (0.666) | |||||
| Paciencia | 4.448 | -4.771 | 1.187 | 0.425 | ||||
| (3.784) | (3.083) | (4.408) | (0.575) | |||||
| Riesgo | -9.688 | 2.880 | -4.962 | -0.205 | ||||
| (6.202) | (8.841) | (9.744) | (1.215) | |||||
| Edad | 2.259* | 1.325 | -0.995 | -0.054 | ||||
| (1.315) | (1.207) | (1.496) | (0.172) | |||||
| Rep. múltiple cursos | 2.792 | -0.438 | 1.640 | 0.068 | ||||
| (4.328) | (2.772) | (3.794) | (0.481) | |||||
| Constante | 7.656** | -22.829 | 9.108** | -9.000 | 15.167** | 26.217 | 1.702** | 1.938 |
| (3.782) | (19.600) | (4.023) | (16.659) | (6.329) | (27.330) | (0.849) | (3.217) | |
| Observaciones | 203 | 190 | 203 | 190 | 203 | 190 | 203 | 190 |
| 0.022 | 0.052 | 0.038 | 0.063 | 0.042 | 0.054 | 0.065 | 0.089 | |
| EF escuela | Sí | Sí | Sí | Sí | Sí | Sí | Sí | Sí |
| Controles | No | Sí | No | Sí | No | Sí | No | Sí |
| Nota: Errores estándares en paréntesis. Los asteriscos denotan significancia estadística: *** p<0.01, ** p<0.05, * p<0.1 | ||||||||
TABLA A5. Estimación del efecto duradero de la repetición sobre Clustering, basándose en el análisis de regresión múltiple.
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
|---|---|---|---|---|---|---|---|---|
| Amigos | Amigos | Mejores amigos | Mejores Amigos | Enemigos | Enemigos | Peores enemigos | Peores enemigos | |
| Repetidor | 0.018 | -0.024 | -0.099 | -0.119* | 0.069 | 0.067 | 0.039 | 0.038 |
| (0.035) | (0.036) | (0.062) | (0.065) | (0.052) | (0.056) | (0.041) | (0.047) | |
| Mujer | 0.023 | 0.012 | -0.005 | -0.023 | ||||
| (0.031) | (0.057) | (0.045) | (0.034) | |||||
| CRT | 0.112* | 0.002 | -0.121 | -0.042 | ||||
| (0.067) | (0.110) | (0.074) | (0.051) | |||||
| GPA | -0.112** | -0.156* | 0.036 | 0.069 | ||||
| (0.047) | (0.091) | (0.064) | (0.063) | |||||
| Paciencia | -0.097* | 0.050 | -0.047 | -0.021 | ||||
| (0.051) | (0.093) | (0.067) | (0.038) | |||||
| Riesgo | 0.134 | 0.173 | -0.198 | -0.108 | ||||
| (0.121) | (0.170) | (0.128) | (0.102) | |||||
| Edad | -0.027** | -0.023 | 0.004 | -0.002 | ||||
| (0.014) | (0.028) | (0.020) | (0.016) | |||||
| Rep. múltiple cursos | 0.065 | -0.052 | -0.003 | 0.048 | ||||
| (0.046) | (0.095) | (0.066) | (0.058) | |||||
| Constante | 0.753*** | 1.168*** | 0.687*** | 0.982** | 0.154** | 0.254 | 0.014 | 0.114 |
| (0.039) | (0.239) | (0.107) | (0.455) | (0.069) | (0.325) | (0.028) | (0.255) | |
| Observaciones | 203 | 190 | 203 | 190 | 203 | 190 | 203 | 190 |
| 0.167 | 0.213 | 0.069 | 0.090 | -0.009 | -0.034 | -0.013 | -0.036 | |
| EF escuela | Sí | Sí | Sí | Sí | Sí | Sí | Sí | Sí |
| Controles | No | Sí | No | Sí | No | Sí | No | Sí |
| Nota: Errores estándares en paréntesis. Los asteriscos denotan significancia estadística: *** p<0.01, ** p<0.05, * p<0.1 | ||||||||
Referencias bibliográficas
Alfonso, A., Brañas-Garza, P., Jorrat, D., Lomas, P., Prissé, B.,
Vasco, M., & Vázquez-De Francisco, M. J. (2023). The adventure of
running experiments with teenagers.
Angerer, S., Bolvashenkova, J., Glätzle-Rützler, D., Lergetporer, P.,
& Sutter, M. (2023). Children’s patience and school-track choices
several years later: Linking experimental and field data.
Ballester, C., Calvó‐Armengol, A., & Zenou, Y. (2006). Who´s who
in networks. Wanted: The key
player.
Bramoullé, Y., Galeotti, A., & Rogers, B. (2016). The Oxford Handbook of the Economics of Networks, Oxford: Oxford University Press.
Brañas-Garza, P., Estepa-Mohedano, L., Jorrat, D., Orozco, V., &
Rascón-Ramírez, E. (2021). To pay or not to pay: Measuring risk
preferences in lab and field.
Brañas-Garza, P., Jorrat, D., Espín, A. M., & Sánchez, A. (2023).
Paid and hypothetical time preferences are the same: Lab, field, and
online evidence.
Brañas-Garza, P., Kujal, P., & Lenkei, B. (2019a). Cognitive
reflection test: Whom, how, when.
Brañas Garza, P. E., Espín, A. M., & Jorrat, D. (2019b). Midiendo
la paciencia.
de Witte, K., Cabus, S., Thyssen, G., Groot, W., & van den Brink,
H. M. (2013). A critical review of the literature on school dropout.
Dohmen, T., Falk, A., Huffman, D., Sunde, U., Schupp, J., &
Wagner, G. G. (2011). Individual risk attitudes: Measurement,
determinants, and behavioral consequences.
Falk, A., Becker, A., Dohmen, T., Enke, B., Huffman, D., & Sunde,
U. (2018). Global evidence on economic preferences.
Freeman, J., & Simonsen, B. (2015). Examining the impact of
policy and practice interventions on high school dropout and school
completion rates: A systematic review of the literature.
Frederick, S. (2005). Cognitive reflection and decision making.
García-Pérez, J. I., Hidalgo-Hidalgo, M., & Robles-Zurita, J. A.
(2014). Does grade retention affect students’ achievement? Some evidence
from Spain.
Golsteyn, B. H., Grönqvist, H., & Lindahl, L. (2014). Adolescent
time preferences predict lifetime outcomes.
González-Betancor, S. M., & López-Puig, A. J. (2016). Grade
retention in primary education is associated with quarter of birth and
socioeconomic status.
González-Rodríguez, D., Vieira, M. J. & Vidal, J. (2019). Factors
that influence early school leaving: a comprehensive model.
Jacob, B. A., & Lefgren, L. (2009) The effect of grade retention
on high school completion.
Jackson, M. (2019). Social and Economic Networks. Princeton: Princeton University Press.
Jann, B. (2017). kmatch: Kernel matching with automatic bandwidth selection. Stata Users´ Group Meetings 2017 11, UK.
López, L., González-Rodríguez, D., & Vieira, M-J. (2023).
Variables que afectan la repetición en la educación obligatoria en
España.
Manacorda, M. (2012). The cost of grade retention.
MEyFP, Ministerio de Educación y Formación Profesional (2024).
OCDE (2024).
Ruiz-García, M., Ozaita, J. Pereda, M., Alfonso, A., Brañas-Garza,
P., Cuesta, J.A., & Sanchez, A. (2023). Triadic influence as a proxy
for compatibility in social relationships,
Tafreschi, D., & Thiemann, P. (2016). Doing it twice, getting it
right? The effects of grade retention and course repetition in higher
education.
Thomson, K. S., & Oppenheimer, D. M. (2016). Investigating an
alternate form of the cognitive reflection test.
Vasco, M., Alfonso, A., Arenas, A., Cabrales, A., Cuesta, J. A.,
Espín, A. M., ... & Brañas Garza, P. (2025). Economic preferences
and cognitive abilities among teenagers in Spain.
Vasco, M. & Vazquez, MJ. (2025). The Gumball machine. PLoS ONE, en prensa.
Información de contacto / Contact info: Pablo Brañas-Garza. Universidad
Loyola Andalucía, Loyola Behavioral Lab. E-mail: