Grade retention, socioeconomic determinants, and research quality

Repetición escolar, determinantes socioeconómicos y calidad de las investigaciones

https://doi.org/10.4438/1988-592X-RE-2025-409-687

Rubén Fernández-Alonso

Universidad de Oviedo

https://orcid.org/https://orcid.org/

Laura M. Cañamero

Universidad de Oviedo

https://orcid.org/0000-0001-5828-004X

Álvaro Postigo

Universidad de Oviedo

https://orcid.org/https://orcid.org/

José Carlos Nuñez

Universidad de Oviedo

https://orcid.org/https://orcid.org/

Abstract

Keywords:

repetition, education, socio-economic status, hierarchical models, propensity score

Resumen

Palabras clave:

Introduction

Grade repetition is an educational measure rooted in the 19th century. Graded schooling made mass education feasible in the emerging liberal states, and repetition became the standard response for students who deviated from group homogeneity or failed to meet academic expectations (Shepard & Smith, 1989). It has been a controversial measure since its inception, as indicated by the earliest work (Ayres, 1909), compendiums of research in the first half of the 20^th century (Goodlad, 1954; Jackson, 1975), and by what is probably the first monograph on the topic published by the California Journal of Elementary Education (Heffernan et al., 1952). These seminal studies quickly identified the causes of repetition, mostly associated with individual factors: poor academic performance, deficits in cognitive functioning, socioemotional maladjustment, and behavioural or health problems. All of those remain as causes, as indicated to a greater or lesser extent by quantitative meta-analysis (Goos et al., 2021; Holmes, 1989; Holmes & Matthews, 1984; Jimerson, 2001a) and systematic qualitative reviews (Biegler & Green, 1993; Jimerson, 2001b; Shepard & Smith, 1990, Valbuena et al., 2021; Xia & Kirby, 2009). This means that any study into grade repetition must consider these factors in its analysis.

A second explanatory source of grade repetition lies in certain socio-demographic, family, and contextual characteristics. These include being male, an immigrant, or younger than one’s peers; coming from broken homes, reconstructed, or more diverse families; and having fewer economic and cultural incentives and resources (Cordero et al., 2014; Organisation for Economic Co-operation and Development [OECD], 2016; Urbano & Álvarez, 2019; Xia & Kirby, 2009). The present study focuses on examining the relationship between repetition and this second source of variation.

Various findings indicate that repetition is conditioned by culture. For example, the extent of repetition varies widely between countries, reflecting each society’s acceptance or rejection of the measure (e.g., OECD 2010, 2016). There are also differences in countries’ regulations concerning it (European Education and Culture Executive Agency, 2011) and how they manage student diversity, which seems to be associated with the effectiveness of the measure (Goos et al., 2021). Lastly, the effects of repetition seem to depend on the palliative measures that are available: in some education systems, repetition is not accompanied by additional support, whereas in others there are alternative complementary actions or special programmes (Fernández-Alonso et al., 2022¸Valbuena et al., 2021). This is justification for focusing the rest of this review on the Spanish context.

Compared to the English-speaking world, Spanish research on grade repetition is very recent, and has mostly been undertaken thanks to data produced by large-scale national (e.g., López-Agudo et al., 2024) and international evaluations (e.g., Agasisti & Cordero, 2017; Blanco-Varela & Amoedo, 2025). The conclusions about the relationship between repetition and social status do not seem to be unanimous. Duran-Bonavila et al. (2024) found that social status lost its predictive capacity over repetition when cognitive skills were controlled for, and Fernández and Rodríguez (2008) noted that socioeconomic level stopped being statistically significant when the results in PISA were considered. Along similar lines, Carabaña (2011) indicated that repetition was not a classist measure, and that it could be explained by what may be logically expected to explain it: school performance, also measured with PISA scores.

Nonetheless, Spanish research has mostly concluded that there is an inverse relationship between measures of social status and the probability of grade repetition (Arroyo et al., 2019; Cabrera et al, 2019; Carabaña, 2013, 2015; Choi et al., 2018; Cobreros & Gortazar, 2023; Cordero et al., 2014; García-Pérez et al., 2014; González-Betancor & López-Puig, 2016; López-Rupérez et al., 2021). However, within this group, estimations of the strength of the relationship vary. For example, Arroyo et al. (2019, p. 85) stated that for repetition, the preponderance of socioeconomic variables was not clear, while Carabaña (2015, p. 24) noted that social determinants were much less important in explaining repetition. At the other extreme, Cobreros & Gortazar (2023) and the OECD (2016) concluded that, for equal levels of competency, the 25% of students from the lowest socioeconomic level were almost four times more likely to repeat a grade than the 25% of students from the highest socioeconomic level. The data from Choi et al. (2018) allow us to estimate that the probability repeating a year for a student at the median of the lower quartile of social status is 4.4 times higher than students at the median of the upper quartile. Official reports, which generally contain descriptive analyses, offer even more sobering estimations that are compatible with a system that is highly reproductive of inequalities in school access (Instituto Vasco de Evaluación e Investigación Educativa [IVEI], 2009). The High Commission for Child Poverty [Alto Comisionado contra la Pobreza Infantil] (2020) warned that one out of every two students in the first income quartile would repeat a grade during compulsory education, whereas in students from higher income households that figure was less than one in ten. Furthermore, the Education Department of Asturias [Consejería de Educación del Principado de Asturias] concluded that 60% of repetitions were concentrated in the 30% of students from the lowest social strata.

This variability of results, which is less than useful for designing educational policy, may at least in part be explained by the quality of study designs: studies with little control over selection bias and covariable adjustment tend to overestimate the adverse effects of repetition (Allen et al., 2009; Jackson, 1975; Lorence, 2006). In Spain, with few exceptions (López-Agudo et al., 2024; Rodríguez-Rodríguez, 2022), most research on repetition has been based on cross-sectional designs (Choi et al., 2018), where the main independent variable (generally results of an external test) is measured after the dependent variable (Carabaña, 2015). This may contaminate the conclusions, as it is impossible to ensure group equivalence (repeaters and non-repeaters) before the repetition, thus introducing selection bias into the calculations.

The aim of the present study is to estimate the probability of repetition for three groups of sociocultural status. Although this is not an original objective, our study provides a new perspective in two ways. Firstly, it uses a database that meets all of the desired characteristics for a high-quality study on repetition (Goos et al., 2021; Valbuena et al., 2021): it deals with a representative sample, it has a set of substantive covariables measured pre- and post-repetition, and it uses propensity matching analysis to minimise selection bias before repetition.

Secondly, the aforementioned characteristics of the database allow for an additional, novel objective in the literature on repetition in Spain: showing how variations in plans of analysis of the same data offer different estimations of the strength of the relationship between repetition and sociocultural status. To that end, the results of three models will be compared:

• Model 1: descriptive. Does not include control variables and reproduces the calculations in official reports (e.g., IVEI, 2009) and lower quality analyses.
• Model 2: cross-sectional. Recreates the results of the most usual analytical-methodological approach in Spanish research: multivariate regression analysis of an ex post facto descriptive design (e.g., Cobreros & Gortazar, 2023) with post-repetition adjustment of covariables.
• Model 3: longitudinal. This is the highest quality design as it includes a dual control: post-repetition adjustment of covariables and pre-repetition matching of groups to minimise selection bias (Krestschmann et al., 2019).

To the best of our knowledge, there are no studies in Spain to date that have included dual control pre- and post-repetition on a single sample. In light of previous evidence (e.g., Allen et al., 2009) the model with least control of bias is expected to show greater effects, in other words to overestimate the probability of low social status students repeating a year. In contrast, better experimental control is expected to demonstrate more moderate effects, which in certain conditions may even dilute statistical significance.

Method

The initial sample was made up of the 7,479 students who in practice comprised the student population in the 4^th year of primary education in the Principality of Asturias in academic year 2008/09. All students were assessed at two timepoints, in the 4^th year of primary and in the 2^nd year of secondary education (ESO), labelled T1 and T2. In order to achieve as homogeneous a sample as possible, the following cases were removed from the original sample: students with insufficient information from before T1 (N = 100); those who repeated a year before T1 (N = 677); those who repeated at the end of their 4^th year of primary, i.e., six weeks after T1 (N = 140); and those who did not participate at T2 either because they had moved or they were absent on the day (N = 554). The final sample comprised 5,999 students, all born in 1999, who were the same age and in the same school year at T1. Out of that sample, 762 would repeat a year between T1 and T2.

Information for this study came from three sources: administrative records, cognitive tests, and student context questionnaires.

Repetition condition, a binary variable (1 = having repeated a year between T1 and T2) extracted from the records of the Asturias Department of Education.

Eight sociodemographic variables were considered. Two were at the individual level, from the administrative records: gender (1 = Girl) and nationality (1 = Immigrant). The rest were school variables measured at T1 and T2: school type (1 = Public school), proportion of migrant children (yMigrant_T1 and yMigrant_T2), and the mean ISEC score (yZISEC_T1 and yZISEC_T2).

Schooling and academic performance were defined with 12 variables. The schooling measure was Change of school between T1 and T2, which was dichotomous (1 = yes). The remainder were measures of academic performance which included Grades in Spanish, Mathematics, and English at T1 and T2, which were also averaged to produce a Grade Point Average score (ZGPA_T1 and ZGPA_T2). The eight grade variables were standardised on an N(0,1) scale and in the multilevel analysis on the school means, so that positive values indicated performance above the school average. Finally, to measure cognitive achievement at T1, the study included scores in the 2009 Diagnostic Assessment, which evaluated three skills: Communication in English, Learning to Learn, and Social and Civic Skills (Test_ENG, Test_LtL and Test_CIV)1. These scores were calculated via models derived from Item Response Theory (unidimensional logistic models with 2 and 3 parameters) using Parscale 4.1 software (du Toit, 2003). The scores were expressed on a scale N(500,100). The 11 academic performance variables were averaged by school to give a proxy of the school’s mean level.

Two socio-emotional variables were considered: self-concept and academic effort. Students completed a context questionnaire containing five statements such as, “I learn lessons easily”. Each statement was scored on a four-point Likert type scale: never or almost never; sometimes; usually; always or almost always. The responses were used to construct the academic self-concept scale (ZSelf-Concept_T1 and ZSelf-Concept_T2) which at T1 was essentially unidimensional: the first factor explained 66.55% of the variance; optimal implementation of parallel analysis recommended a single dimension; and both the indices of unidimensionality (UNICO = .999, ECV = .982, MIREAL = .090; Calderón-Garrido et al., 2019) and fit were good. Despite the small number of items, the scale seemed consistent between the two timepoints (T₁: α = .87, ω = .88; T₂: α = .91; ω = .91). The ZSelf-Concept_T1 and ZSelf-Concept_T2 scores were expressed on a normal scale [N(0,1)], where positive values indicated good academic self-concept.

Lastly, the academic effort variable (ZAcademic-Effort_T1 and ZAcademic-Effort_T2) was constructed from the response to five statements such as: “I finish my tasks even if they are difficult”. Students’ levels of agreement with each statement was scored the same way as for self-concept. Despite having few items, the scale demonstrated high internal consistency (T₁: α = .80, ω = .80; T₂: α = .77, ω = .78). At T1, the first factor explained 55.5% of the total variance and exhibited excellent indices of fit (GFI = .999, RMSR = .022; Calderón-Garrido et al., 2019). The psychometric properties at T2 were similar: the first factor explained 52.6% of the variance and the indices of fit were very good (GFI = .998, RMSR = .029). Factor loadings of all items ranged between .523 and .748, which confirmed that the scale was essentially unidimensional at both timepoints (Postigo et al., 2021a, b). Evidence of validity of internal structure and reliability of the scores was examined using FACTOR.12.04.04 software (Ferrando & Lorenzo-Seva, 2017

Procedure

The study is a secondary exploitation of the Asturian Educational Diagnostic Evaluation [Evaluación de Diagnóstico Educativo del Principado de Asturias], a testing program run by the regional educational department. The responsibilities were assigned as follows: school management managed application of the assessments within each school; the school inspection service performed quality control for the program; and the evaluation service coded and analysed the data.

ata analysis

As noted previously, in order to mitigate the biases inherent to all studies on repetition, this study used a dual control strategy: matching scores and fitting multilevel models.

Scores were matched via propensity score matching analysis (PSM), which is the most widely used approach in psychoeducational research on repetition (Krestschmann et al., 2019; Wu et al., 2010;). The aim is to match an experimental group (repeaters) with a control group (non-repeaters) so that they are equivalent before the treatment (repetition) (Stuart, 2010; Zhao et al., 2021). PSM follows a series of steps (Ho et al., 2011) that can be summarised in three stages: planning, execution, and evaluation of results.

The following matching variables were first selected for T1: (1) sociodemographic factors, Girl, Immigrant, Public_School_T1 and yZISEC_T1; (2) proxies of prior achievement, scores in Spanish, English, and Mathematics at T1, the grade point average (ZGPA_T1), and the scores in the 2009 Asturian Diagnostic Evaluation; (3) socio-emotional measures, ZSelf-Concept_T1 and ZAcademic-Effort_T1. All of the attitudinal and performance measures were considered at the individual and at the school level. Girls tend to exhibit better performance than boys in communicative-linguistic areas (Mullis et al., 2023) and usually make more effort academically (Postigo et al., 2021a), although they tend to see themselves as less competent, especially in maths (Mejía-Rodríguez et al., 2021). In addition, publicly funded schools demonstrate lower school performance and higher numbers of migrant children and repeaters (Instituto Nacional de Evaluación Educativa, 2019). Because of that, the matching also included the interactions between these variables. In summary, the propensity scores were estimated using a model with 27 covariables and 16 terms of interaction between variables.

In the execution phase, students in each group were matched based on their propensity scores, which were expressed as the conditional probability of receiving treatment (i.e., repeating) given the vector of specific covariables (Zhao et al., 2021). There are a range of matching methods, and the literature recommends comparing various options and choosing the one which offers the best balance (Austin, 2014). In this case we compared two types of algorithms. The first were matching methods of one-to-one cases: nearest neighbour without replacement, optimal pair matching, and genetic matching. The second type were algorithms that used non-uniform weighting: nearest neighbour with replacement, generalised full matching, and subclassification. To improve the matching balance, and depending on the possibilities offered by each method, customisations were included such as matching in specific order, restricting the distance between pairs, or matching with k > 1.

Finally, the matching method was selected based on two criteria: balance strength and sample size. Each criterion minimises one type of bias which are occasionally in opposition: treatment effect and sample selection. Better balance indicates suitable matching and therefore less bias when estimating the effect of the treatment. However, if severe restrictions are needed to achieve robust matching (such as only matching cases with small differences in propensity scores), that would increase the likelihood of excluding matches, which may introduce sample selection bias or bias due to incomplete matching. In the present study, balance was considered satisfactory when the standardised differences between groups, and the differences in the empirical cumulative distribution function (eCDF) were close to zero; and the ratio of variances were close to one. Bias due to incomplete matching was assessed using the percentage of discarded, unmatched cases and the size of the effective sample achieved by each algorithm. The matching was done using the Matching package (Sekhon, 2011), and evaluation of balance used Cobalt (Greifer, 2023), both in R (R Core Team, 2023).

School phenomena are multilevel and, logically, each level of the hierarchy has a different variability and errors are not independent (Gaviria & Castro, 2005). Hierarchical or multilevel models are specifically developed to analyse data with a nested structure and address the problem of the “design effect” in cases where errors are not independent (Fernández-Alonso & Muñiz, 2019). In addition, because the dependent variable in the study is binary, it is unrealistic to assume normality. Because of that, we used the multilevel binary logistic model (Bernouilli), which allows use of various types of predictor variables (continuous, discreet, binary…) in all levels of analysis.

As noted at the end of the Introduction, three models were specified in this study. Model 1, which estimated the probabilities of each ISEC group repeating without control variables, has two functions: it serves as a comparison for the other models and recreates the raw estimations from the descriptive analysis. Model 2 includes the sociodemographic, school, cognitive, and socio-emotional variables measured at T2 and reproduces the estimations of a cross-sectional design—the most common design in Spanish research on repetition. Model 3 adds the weightings from matching groups prior to repetition and therefore has a double statistical control: adjustment of post-repetition covariables from the cross-sectional design, and matching groups pre-repetition (Krestschmann et al., 2019).

The results of these models are presented in terms of odds and odds ratios (OR). The latter allow us to compare the odds of different values of an independent variable, quantifying and indicating the direction of the association between the dependent variable and its predictors in the binary logistic regression. The analysis was done using HLM 7.0 (Raudenbush et al., 2011). 

The amount of missing data ranged from 0% to 12% depending on the variable. Data was recovered in two stages: where a case had incomplete data in one variable, the missing data was replaced with the subject mean. For completely missing values, we used the Expectation-Maximization algorithm with auxiliary variables offered by SPSS 24 (IBM, 2016). Fernández-Alonso et al. (2012) showed that this two-stage process is the best for recovering missing data when, as in this case, the size of the missing data is small and the bias is moderate.

Results

Before presenting the results of the adjusted models, it is necessary to offer evidence of the quality of the group matching at T1. This is fundamental for interpreting the comparison of the subsequent models, especially model 3, where it is assumed that the correlation between repetition and predictors in T1 (pre-repetition) is equal to 0.

The two best-balanced matching procedures were nearest neighbour without replacement (NN), from the one-to-one matching algorithms, and generalised full matching (GFM) from the non-uniform weighting algorithms. Ultimately, GFM was chosen because, unlike NN, it allows all the cases in the control group to be used, which is a preferred criteria when two matching procedures offer similar balance (Sävje et al., 2021). The matched sample was made up of 762 repeaters and 5237 non-repeaters, which is equivalent to an effective control sample of 395 cases.

Figure 1 shows the differences in standardised means between the groups before and after matching. Before matching, the circles indicate highly significant differences, with higher scores generally for the non-repeater group. For example, the difference in school grades was around 1.5 standard deviations. With this imbalance it would be impossible to determine whether potential differences found at T2 were due to having repeated a year or merely indicative of an initial discrepancy.

FIGURE I. Difference in means (Z scores) between the groups before and after matching.

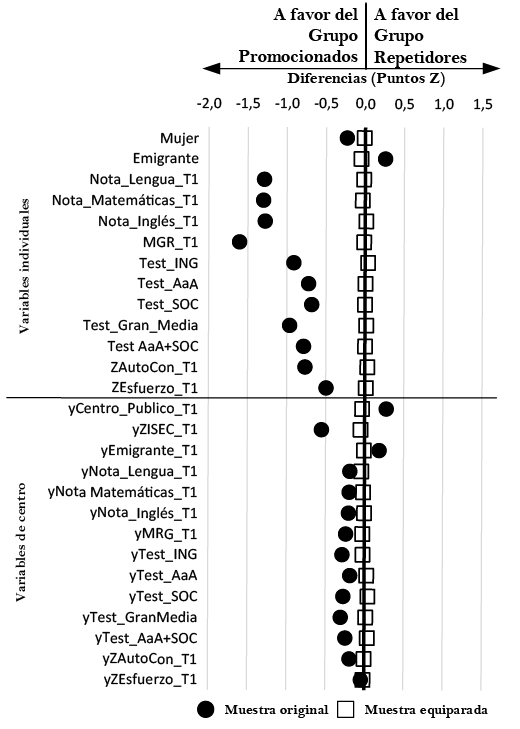
Note. GPA = Grade Point Average; ENG = English; LtL = Learn to Learn; CIV = Social and Civic Skills; ISEC = Socioeconomic and cultural index.

Source: Compiled by the authors.

The squares show the differences after matching. All differences were smaller than |0.1|, hence the markers are around the value of Z = 0. The statistical matching created two groups that were comparable before any repetition in terms of previous performance, socio-emotional traits, and sociodemographic characteristics. This will allow us to discount any differences that may be found at T2 as being related to the matched variables at T1, minimising the bias of selecting the groups to compare.

Table 1 shows the results of the descriptive model. The intercept (-1.94) corresponds to the logit of ISEC_Medium, which had a low associated probability of repetition (OR = 0.14), and was quite precise given the narrow confidence intervals. The OR for the High_ISEC group (0.17) indicates a probability of repetition that was approximately 85% lower than the reference group, while the students in the Low_ISEC group were more than twice as likely to repeat a year than the Medium group and almost 13 times more likely (2.11 / 0.17) than the High group.

TABLE I. Model without adjustment covariables: prediction of repetition

Table II shows the estimations of the cross-sectional model. On including the control variables, the probability of the Medium_ISEC group repeating fell by almost two thirds (OR = 0.06). The OR of the High group practically doubled (0.30), indicating that the probability of repeating fell by 70%, while in the Low_ISEC group, the probability of repeating was approximately 66% higher than the reference group, and 5.5 times higher than the High_ISEC group.

TABLE II. Cross-sectional model: prediction of repetition

The main change in the longitudinal model (Table III) was in students in the Low_ISEC group. The coefficient was on the edge of statistical significance and the probability of them repeating was only 3% greater than the Medium_ISEC group. The effect when comparing the two extreme groups was also much reduced, practically by half. The OR of the Low_ISEC group was 2.4 times greater than the High_ISEC group. Some covariables at T2 lost their statistical significance due to the effect of the statistical matching at T1.

TABLE III. Longitudinal model: prediction of repetition

Figure II shows an alternative way of comparing the models’ estimations. It shows the probability of each group repeating according to each model. The longitudinal model is the one that most reduces the probabilities of the Low and Medium groups repeating, while the probability of the High group repeating is relatively stable.

FIGURE II. Probability of repeating by model and ISEC group

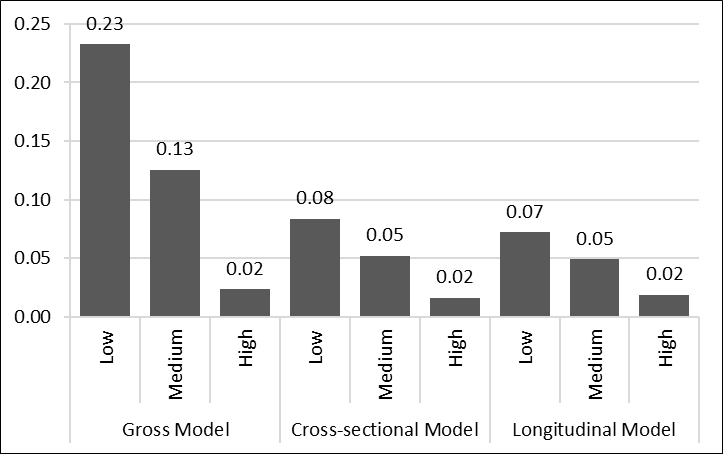
Source: Compiled by the authors.

Discussion

Educational research has mostly identified a negative relationship between indicators of social status and the likelihood of repetition. However, the conclusions have not been unanimous (e.g., Fernández & Rodríguez, 2008). Furthermore, in the studies that have found significant relationships, the estimations of the strength of the association have been varied (e.g., Carabaña, 2015; Cobreros & Gortazar, 2023). One plausible reason for these differences may lie in the design of these studies, as insufficiently controlling bias has been well documented to tend to lead to overestimation of the negative effects of repetition (Lorence, 2006).

In this context, the present study compared the probability of repetition according to socioeconomic and socio-cultural status, using a single database to estimate three analytical models that simulated a range of study designs: (1) descriptive, without controlling variables; (2) cross-sectional, with control of covariables post-repetition; and (3) longitudinal, with double control of bias, both pre- and post-repetition. To the best of our knowledge, this is the first study of its kind in Spanish research on the association between repetition and social status. The comparison was possible because the study was able to use a high-quality database allowing simulation of analysis conditions, gradually incorporating increased control of biases associated with repetition.

In line with most previous research (e.g., Choi et al., 2018; Cordero et al., 2014; García-Pérez et al., 2014; López-Rupérez et al., 2021), the study indicated that repetition is affected by social class. This has also been confirmed by research in various different education systems (e.g., Bastos & Ferrão, 2019; Ferrão et al., 2017; Klapproth & Schaltz, 2015; Salza, 2022; Xia & Kirby, 2009). However, our data suggest that, at least in the Spanish context, there is nuance to the relationship between repetition and social class. As one might expect, socio-cultural status had a strong impact on the probability of repetition in the descriptive model. Students in the Low ISEC group were more likely to repeat a year than their classmates in the Medium ISEC group, while those students in the High ISEC group were significantly more protected against the risk of repetition. Model 2 reproduced the estimations of cross-sectional analysis, the most common design in Spanish research. All of the covariables at T2 were significant, and once they were controlled for, the probability of Low_ISEC students repeating was 5.5 times higher than High_ISEC students doing so. This is similar to the calculations for Asturias (6.2 times higher) using data from the two most recent PISA tests (Cobreros & Gortazar, 2023).

The third model produced interesting changes, which can be summarised in three conclusions. Firstly, compared to the cross-sectional model (Model 2), the longitudinal model (Model 3) reduced the difference in probabilities of repetition between the two extreme ISEC groups (Low vs. High) by 56%, from 5.5 times to 2.4 times. This would seem to confirm that better control of biases produces more conservative estimations of repetition’s negative effects (Allen et al., 2009). Although there are Spanish studies that have gone beyond adjusting for covariables in descriptive ex post facto designs (e.g., Rodríguez-Rodríguez, 2022), the evidence from our study suggests the need to perform studies that consider all potential sources of bias when studying repetition (Goos et al., 2021; Valbuena et al., 2021).

Secondly, in the longitudinal model, the difference in Odds Ratios between the Low and Medium ISEC groups practically disappeared. This adds detail to previous conclusions on the relationship between repetition and social class. There is some consensus (e.g., Carabaña, 2015; García-Pérez et al., 2014) that repetition tends to be concentrated in children of mothers with little education, or in the minority whose parents had very low levels of education. Our data indicate an alternative interpretation, as the Low and Medium ISEC groups had very similar probabilities of repeating a year. In the Spanish context, where around a third of the school population repeat a year, this is not really surprising; with such a proportion, it would be unlikely that the middle class would be spared. So in light of the results of the longitudinal model, it seems more correct to say that in Spain, any child may end up having to repeat a year, except those from high socio-cultural status households.

Lastly, apart from the effect of social status, the longitudinal model identified two highly significant personal variables at T2, school grades and academic effort. In other words, the two fundamental criteria used by teaching teams to propose repetition. In this regard, the model offers a picture that is consistent with what one would expect (Carabaña, 2011).

These details should not hide the fact that our study’s overall conclusion is concerning. In Spain, given the same levels of learning difficulties, levels of effort, and other sociodemographic characteristics, social class has a different impact on teachers’ proposals for repetition. This should invite reflection about the context these decisions are made in and the consequences for equality in the system. Repetition is categorised as an extraordinary attention to diversity measure. However, something that affects 30% of students should not be considered so extraordinary. Our results reiterate the need to make such decisions cautiously in order to not contribute to increasing inequality in terms of accessing and remaining in the education system, or, as our data suggest, not reproducing the privileged situation of the minority with the highest socio-cultural status.

Finally, the data from our study must be interpreted in light of various limitations. Firstly, the two measurements were taken four school years apart. Having an intermediate timepoint would have allowed better monitoring of schooling pathways. Such a long time between the two timepoints may have allowed variations to be introduced that could have affected the results (Kretschmann et al., 2019). In addition, although the set of adjustment variables was relatively large, there were no specific measures of cognitive abilities and social relationships, and it was therefore impossible to know any effects of these types of variables, which seem to modulate the relationship between repetition and social status (Duran-Bonavila et al, 2024; Wu et al., 2010). Furthermore, the socio-emotional measures used in the study (self-concept and effort) were self-reported by the students, with all of the items worded positively. This means being unable to discount acquiescence bias in the socio-emotional scores (Hernández-Dorado et al., 2025; Primi et al., 2019). To address these limitations, future studies on repetition in Spain will need to use specific study designs that include following cohorts throughout their schooling and repeated measures pre- and post- repetition. This means designs using matched samples or some quasi-experimental approach (regression discontinuity, methods based on instrumental variables, or difference-in-difference analysis) and connecting repetition with medium- to long-term results, such as early dropout from education or employment outcomes.

In countries with high rates of repetition, such as Spain, there is a culture of repetition—the shared belief that repetition is a good thing (European Education and Culture Executive Agency, 2011). However, the evidence indicates that it has a high social and economic cost, without clear academic benefits (Goos et al., 2021). In any case, having evidence will not automatically change teaching practice (IVEI, 2009), meaning that more equitable and effective alternatives are required (Consejería de Educación del Principado de Asturias, 2016). To bring the Spanish education system into line with international rates of repetition (e.g., OCDE, 2016), five strategies have been proposed, which will be particularly beneficial to the more vulnerable students (Fernández-Alonso et al, 2022). First, change repetition to match the exceptional nature current legislation describes it as having—current legislation has removed a set number of failed courses as criteria for automatic repetition and instead promotes collective decision-making based on how important the failed subjects are and expectations for recovery and success in the next school year. It is also essential to reinforce early detection of academic difficulties, through individualised alert and support systems, avoiding the situation of poor performance leading to repetition, especially in secondary education, where the measure in most cases is not used for prevention. Thirdly, teachers should use teaching methods that are adapted to diversity, such as differentiated teaching and cooperative learning, together with expanded programs for educational reinforcement, specialist tutors, and extra-curricular resources. Teacher training needs to prioritise formative assessment and inclusive teaching so that the response to diversity is not repetition. Finally, there needs to be flexibility in the curricular structure and the organisation in schools, allowing schooling to be tailored and adaptive advancement for students.

Supplementary Material

This paper has online supplementary material, which provides details of the PSM analysis (comparison of matching algorithms, evaluation of balance, and code examples): https://osf.io/nq7c3/files/osfstorage

Notes

Referencias bibliográficas

Agasisti, T., & Cordero, J. M. (2016). The determinants of repetition rates in Europe: Early skills or subsequent parents’ help? Journal of Policy Modeling, 39(1), 129–146. https://doi.org/10.1016/j.jpolmod.2016.07.002

Allen, C. S., Chen, Q., Willson, V. L., & Hughes, J. N. (2009). Quality of research design moderates effects of grade retention on achievement: A meta-analytic, multi-level analysis. Educational Evaluation and Policy Analysis, 31(4), 480–499. https://doi.org/10.3102/0162373709352239

Alto Comisionado contra la Pobreza Infantil (2020). Pobreza infantil y desigualdad educativa en España. Autor.

Arroyo, D., Constante, I. A., & Asensio, I. (2019). La repetición de curso a debate: Un estudio empírico a partir de PISA 2015. Educación XX1, 22(2), 69–92. https://doi.org10.5944/educXX1.22479

Austin, P. C. (2014). A comparison of 12 algorithms for matching on the propensity score. Statistics in Medicine, 33, 1057–1069. https://doi.org/10.1002/sim.6004

Ayres, L. P. (1909). Laggards in our schools. Charities Publication Committee.

Bastos, A., & Ferrão, M. E. (2019). Analysis of grade repetition through multilevel models: A study from Portugal. Cadernos de Pesquisa, 49, 270–288. https://doi.org/10.1590/198053146131

Biegler, C. D., & Green, V. P. (1993). Grade retention: A current issue. Early Child Development and Care, 84, 117–122. https://doi.org/10.1080/0300443930840111

Blanco-Varela, B., & Amoedo, J. M. (2025). Efectos de la repetición escolar según el perfil socioeconómico del estudiante. Revista de Educación, (407), 257–288. https://doi.org/10.4438/1988-592X-RE-2025-407-658

Cabrera, L., Pérez, C., Santana, F. & Betancort, M. (2019). Desafección escolar del alumnado repetidor de segundo curso de Enseñanza Secundaria Obligatoria. International Journal of Sociology of Education, 8(2), 173–203. https://doi.org/10.17583/rise.2019.4139

Calderón-Garrido, C., Navarro-González, D., Lorenzo-Seva, U., & Ferrando, P. J. (2019). Multidimensional or essentially unidimensional? A multi-faceted factor-analytic approach for assessing the dimensionality of tests and items. Psicothema, 31(4), 450–457. https://doi.org/10.7334/psicothema2019.153

Carabaña, J. (2011). Las puntuaciones PISA predicen casi toda la repetición de curso a los 15 años en España. Revista de Sociología de la Educación-RASE, 4(3), 283–303.

Carabaña, J. (2013). Repetición de curso y puntuaciones PISA ¿cuál causa cuál? En Ministerio de Educación, Cultura y Deporte (Ed.), PISA 2012. Programa para la Evaluación Internacional de los Alumnos. Informe Español (Vol. II, pp. 32-66). Autor.

Carabaña, J. (2015). Repetir hasta 4º de Primaria: determinantes cognitivos y sociales según PIRLS. Revista de Sociología de la Educación-RASE, 8(1), 7–27.

Choi, Á., Gil, M., Mediavilla, M., & Valbuena, J. (2018). Predictors and effects of grade repetition. Revista de Economía Mundial, 48, 21–42. https://doi.org10.33776/rem.v0i48.3882

Cobreros, L, & Gortazar, L. (2023). Todo lo que debes saber de PISA 2022 sobre equidad. EsadeEcPol – Save The Children.

Consejería de Educación del Principado de Asturias (2016). La repetición escolar: hechos y creencias. Informes de Evaluación, 2.

Cordero, J. M., Manchón, C., & Simancas, R. (2014). La repetición de curso y sus factores condicionantes en España. Revista de Educación, 365, 13–37. https://doi.org/10.4438/1988-592X-RE-2014-365-263

du Toit, M. (2003). IRT from SSI: BILOG-MG, MULTILOG, PARSCALE, TESTFACT. Scientific Software International.

Duran-Bonavila, S., Rodríguez-Gómez, A., & Becerril-Galindo, M. (2024). Determinants of grade repetition in Spain. Analysis of cognitive and socio-economic, mediated by ethnic factors. International Journal of Educational Psychology, 13(1), 63–85. https://doi.org/10.17583/ijep.12804

European Education and Culture Executive Agency. (2011). Grade retention during compulsory education in Europe. Regulations and statistics. European Commission Publications Office. https://data.europa.eu/doi/10.2797/50570

Fernández, J. J., & Rodríguez, J. C. (2008). Los orígenes del fracaso escolar en España: Un estudio empírico. Mediterráneo económico, 14, 323–349.

Fernández-Alonso, R., Suárez-Álvarez, J., & Muñiz, J. (2012). Imputación de datos perdidos en las evaluaciones diagnósticas educativas [Imputation methods for missing data in educational diagnostic evaluation]. Psicothema, 24(1), 167–175. https://psycnet.apa.org/record/2012-02525-026

Fernández-Alonso, R., & Muñiz, J. (2019). Calidad de los sistemas educativos: modelos de evaluación. Propósitos y Representaciones, 7(spe), e347–347. http://dx.doi.org/10.20511/pyr2019.v7nSPE.347

Fernández-Alonso, R., Postigo, Á., García-Crespo, F. J., Govorova, E., & Ferrer, Á. (2022). Repetir no es aprender. Mitos desmentidos y alternativas posibles a una práctica ineficiente e inequitativa. Save the Children.

Ferrando, P. J., & Lorenzo-Seva, U. (2017). Program FACTOR at 10: Origins, development and future directions. Psicothema, 29(2), 236–240. https://doi.org/10.7334/psicothema2016.304

Ferrão, M. E., Costa, P. M., & Matos, D. A. S. (2017). The relevance of the school socioeconomic composition and school proportion of repeaters on grade repetition in Brazil: A multilevel logistic model of PISA 2012. Large-scale Assessments in Education, 5, 1–13. https://doi.org/10.1186/s40536-017-0036-8

García-Pérez, J. I., Hidalgo-Hidalgo, M., & Robles-Zurita, J. A. (2014). Does grade retention affect students’ achievement? Some evidence from Spain. Applied Economics, 46(12), 1373–1392. https://doi.org/10.1080/00036846.2013.872761

Gaviria, J. L., & Castro, M. (2005). Modelos jerárquicos lineales. La Muralla.

González-Betancor, S. M., & López-Puig, A. J. (2016). Grade retention in primary education is associated with quarter of birth and socioeconomic status. PloS one, 11(11), Article e0166431. https://doi.org/10.1371/journal.pone.0166431

Goodlad, J. I. (1954). Some effects of promotion and non-promotion upon the social and personal adjustment of children. The Journal of Experimental Education, 22(4), 301–328. http://dx.doi.org/10.1080/00220973.1954.11010490

Goos, M., Pipa, J., & Peixoto, F. (2021). Effectiveness of grade retention: A systematic review and meta-analysis. Educational Research Review, 34, 1–14. https://doi.org10.1016/j.edurev.2021.100401

Greifer, N. (2023). cobalt: Covariate Balance Tables and Plots. R package version 4.5.1

Heffernan. H., Gilbertson, E., Greenblatt, E., & Hills, J. A. (1952). What research says about nonpromotion. California Journal of Elementary School, XXI(1), 7–28.

Hernández-Dorado, A., Ferrando, P. J., & Vigil-Colet, A. (2025). The impact and consequences of correcting for acquiescence when correlated residuals are present. Psicothema, 37(1), 11–20. https://doi.org/10.70478/psicothema.2025.37.02

Ho, D. E., Imai, K., King, G., & Stuart, E. A. (2011). MatchIt: Nonparametric Preprocessing for Parametric Causal Inference. Journal of Statistical Software, 42(8), 1–28. https://doi.org/10.18637/jss.v042.i08

Holmes, C. T. (1989). Grade level retention effects: A meta-analysis of research studies. In L. A. Shepard, & M. L. Smith (Eds.), Flunking Grades: Research and Policies on Retention (pp. 16–33). The Flamer Press.

Holmes, C. T., & Matthews, K. M. (1984). The effects of nonpromotion on elementary and junior high school pupils: A meta-analysis. Review of Educational Research, 54(2), 225–236. https://doi.org/10.2307/1170303

Hong, G., & Yu, B. (2008). Effects of kindergarten retention on children´s social-emotional development: an application of propensity score method to multivariate, multilevel data. Developmental Psychology, 44(2), 407–421. https://doi.org/10.1037/0012-1649.44.2.407

Hunt, C. S., & Seiver, M. (2017). Social class matters: Class identities and discourses in educational contexts. Educational Review, 70(3), 342–357. https://doi.org10.1080/00131911.2017.1316240

Instituto Nacional de Evaluación Educativa (2019). PISA 2018 - Programa para la Evaluación Internacional de los Estudiantes. Informe español. Ministerio de Educación y Formación Profesional.

Instituto Vasco de Evaluación e Investigación Educativa (IVEI). (2009) Efecto de las repeticiones de curso en el proceso de enseñanza-aprendizaje del alumnado. Gobierno Vasco.

Jackson, G. B. (1975). The research evidence on the effects of grade retention. Review of Educational Research, 45(4), 613–635. https://doi.org/10.2307/1170067

Jimerson, S. R. (2001a). Meta-analysis of grade retention research: Implications for practice in the 21st century. School Psychology Review, 30(3), 420–437. http://dx.doi.org/10.1080/02796015.2001.12086124

Jimerson, S. R. (2001b). A synthesis of grade retention research: Looking backward and moving forward. California School Psychologist, 6, 47–59. https://doi.org/10.1007/BF03340883

Klapproth, F., & Schaltz, P. (2015). Who is retained in school, and when? Survival analysis of predictors of grade retention in Luxembourgish secondary school. European Journal of Psychology of Education, 30, 119–136. https://doi.org/10.1007/s10212-014-0232-7

Kretschmann, J., Vock, M., Lüdtke, O., Jansen, M., & Gronostaj, A. (2019). Effects of grade retention on students’ motivation: A longitudinal study over 3 years of secondary school. Journal of Educational Psychology, 111, 1432–1446. http://dx.doi.org/10.1037/edu0000353

López-Agudo, L.A., Latorre, C.P. & Marcenaro-Gutierrez, O.D. (2024). Grade retention in Spain: The right way? Educational Assessment, Evaluation and Accountability, 36, 53–74. https://doi.org/10.1007/s11092-023-09421-6

López-Rupérez, F., García-García, I., & Expósito-Casas, E. (2021). La repetición de curso y la graduación en Educación Secundaria Obligatoria en España. Análisis empíricos y recomendaciones políticas. Revista de Educación, 394, 325–353. https://doi.org10.4438/1988-592X-RE-2021-394-510

Lorence, J. (2006). Retention and academic achievement research revisited from a United States perspective. International Education Journal, 7(5), 731–777.

Mejía-Rodríguez, A. M., Luyten, H., & Meelissen, M. R. (2021). Gender differences in mathematics self-concept across the world: An exploration of student and parent data of TIMSS 2015. International Journal of Science and Mathematics Education, 19(6), 1229–1250.

Méndez, I., & Cerezo, F. (2018). La repetición escolar en Educación Secundaria y factores de riesgo asociados. Educación XXI, 21(1), 41–62. https://doi.org/10.5944/educxx1.20172

Michavila, F., & Narejos, A. (2021). Algunas debilidades del sistema educativo español. Ministerio de Educación y Formación Profesional.

Mullis, I. V. S., von Davier, M., Foy, P., Fishbein, B., Reynolds, K. A., & Wry, E. (2023). PIRLS 2021 International Results in Reading. Boston College, TIMSS & PIRLS International Study Center. https://doi.org/10.6017/lse.tpisc.tr2103.kb5342

OECD (2010). PISA 2009 Results (Volume I): What students know and can do – student performance in reading, mathematics and science. OECD Publishing. https://doi.org/10.1787/9789264091450-en

OECD (2016). PISA 2015 Results (Volume I): Excellence and Equity in Education. OECD Publishing. https://doi.org/10.1787/9789264266490-en

Peña-Suárez, E., Fernández-Alonso, R., & Fernández, J. M. (2009). Estimación del valor añadido de los centros escolares. Aula Abierta, 37(1), 3–18.

Postigo, Á., Cuesta, M., Fernández-Alonso, R., García-Cueto, E., & Muñiz, J. (2021a). Academic grit modulates school performance evolution over time: A latent transition analysis. Revista de Psicodidáctica, 26(2), 87–95. https://doi.org/10.1016/j.psicoe.2021.03.001

Postigo, Á., Cuesta, M., Fernández-Alonso, R., García-Cueto, E., & Muñiz, J. (2021b). Temporal stability of grit and school performance in adolescents: A longitudinal perspective. Psicología Educativa, 27(1), 77–84. https://doi.org/10.5093/psed2021a4

Primi, R., Santos, D., De Fruyt, F., & John, O. P. (2019). Comparison of classical and modern methods for measuring and correcting for acquiescence. British Journal of Mathematical and Statistical Psychology, 72(3), 447–465. https://doi.org/10.1111/bmsp.12168

R Core Team (2023). R: A language and environment for statistical computing. R Foundation for Statistical Computing. https://www.R-project.org/

Raudenbush, S. W., Bryk, A. S., Cheong, Y. F., Congdon, R. T., & Du Toit, M. (2011). HLM7 Hierarchical Linear and Nonlinear Modeling. Scientific Software International.

Rodríguez-Rodríguez, D. (2022). Grade Retention, Academic Performance and Motivational Variables in Compulsory Secondary Education: A Longitudinal Study. Psicothema, 34(3), 429–436. https://doi.org/10.7334/psicothema2021.582

Salza, G. (2022). Equally performing, unfairly evaluated: The social determinants of grade repetition in Italian high schools. Research in Social Stratification and Mobility, 77, Article e100676. https://doi.org/10.1016/j.rssm.2022.100676

Sävje, F., Higgins, M., & Sekhon, J. (2021). Generalized Full Matching. Political Analysis, 29(4), 423–447. https://doi.org/10.1017/pan.2020.32

Sekhon, J. S. (2011). Multivariate and propensity score matching software with automated balance optimization: The matching package for R. Journal of Statistical Software, 42(1), 1–52. https://doi.org/10.18637/jss.v042.i07

Shepard, L. A., & Smith, M. L. (1989). Flunking grades: Research and policies on retention. The Falmer Press.

Shepard, L. A., & Smith, M. L. (1990). Synthesis of research on grade retention. Educational Leadership, 47(8), 84–88.

Stuart, E. A. (2010). Matching methods for causal inference: A review and a look forward. Statistical Science, 25(1), 1–21. https://doi.org/10.1214/09-STS313

Timmerman, M. E., & Lorenzo-Seva, U. (2011). Dimensionality assessment of ordered polytomous items with Parallel Analysis. Psychological Methods, 16(2), 209–220. https://doi.org/10.1037/a0023353-

Urbano, A., & Álvarez, L. (2019). La repetición de curso en la adolescencia: Influencia de variables sociofamiliares. HEKADEMOS, 27, 51–59.

Valbuena, J., Mediavilla, M., Choi, Á., & Gil, M. (2021). Effects of Grade Retention Policies: A Literature Review of Empirical Studies Applying Causal Inference. Journal of Economic Surveys, 35(2), 408–451. https://doi.org10.1111/joes.12406

Wu, W., West, S. G., & Hughes, J. N. (2010). Effect of grade retention in first grade on psychosocial outcomes. Journal of Educational Psychology, 102, 135–152. http://doi.org/10.1037/a0016664

Xia, N., & Kirby, S. N. (2009). Retaining students in grade: A literature review of the effects of retention on students’ academic and nonacademic outcomes. RAND Technical Report.

Zhao, Q. Y., Luo, J. C., Su, Y., Zhang, Y. J., Tu, G. W., & Luo, Z. (2021). Propensity score matching with R: conventional methods and new features. Annals of Translational Medicine, 9(9), 812. http://dx.doi.org/10.21037/atm-20-3998

Información de contacto / Contact info: Laura M. Cañamero. Universidad de Oviedo, Facultad de Psicología, Departamento de Psicología. E-mail: lauramcanamero@uniovi.es