Repetición escolar, determinantes socioeconómicos y calidad de las investigaciones

Grade retention, socioeconomic determinants, and research quality

https://doi.org/10.4438/1988-592X-RE-2025-409-687

Rubén Fernández-Alonso

Universidad de Oviedo

https://orcid.org/0000-0002-7011-0630

Laura M. Cañamero

Universidad de Oviedo

https://orcid.org/0000-0001-5828-004X

Álvaro Postigo

Universidad de Oviedo

https://orcid.org/0000-0003-4228-8965

José Carlos Núñez

Universidad de Oviedo

https://orcid.org/0000-0002-9187-1201

Resumen

Palabras clave:

repetición, educación, estatus socio-económico, modelos jerárquicos, análisis de propensión

Abstract

Keywords:

Introducción

La repetición escolar es una medida decimonónica. La escuela graduada posibilitó la escolarización masiva en los emergentes estados liberales y la repetición fue la solución final para el alumnado que se apartaba de la homogeneidad del grupo o no alcanzaba los estándares establecidos (Shepard & Smith, 1989). La medida fue polémica desde su nacimiento, como lo atestiguan los trabajos primigenios (Ayres, 1909), los compendios de la investigación de la primera mitad del siglo XX (Goodlad, 1954; Jackson, 1975) o el que probablemente sea el primer monográfico sobre el tema editado por el California Journal of Elementary Education (Heffernan et al., 1952). Estos estudios seminales pronto identificaron sus causas, mayoritariamente asociadas a factores personales: rendimiento académico bajo, funcionamiento cognitivo deficitario, desajuste socioemocional y conductual o problemas de salud. Todos ellos mantienen plena vigencia, habiéndose replicado, con mayor o menor intensidad, en los metanálisis cuantitativos (Goos et al., 2021; Holmes, 1989; Holmes & Matthews, 1984; Jimerson, 2001a) y en las revisiones sistemáticas cualitativas (Biegler & Green, 1993; Jimerson, 2001b; Shepard & Smith, 1990, Valbuena et al., 2021; Xia & Kirby, 2009). Por tanto, los estudios sobre repetición deberán considerar estos factores en sus análisis.

Una segunda fuente explicativa de la repetición residiría en ciertas características socio-demográficas, familiares y contextuales, tales como: ser hombre; emigrante; más joven que sus iguales; provenir de hogares desestructurados, familias reconstruidas y más diversas; y disponer de menos estímulos y recursos culturales o económicos (Cordero et al., 2014; Organisation for Economic Co-operation and Development [OECD], 2016; Urbano y Álvarez, 2019; Xia & Kirby, 2009). El presente trabajo se centrará en analizar la relación entre repetición y esta segunda fuente de variación.

Por otro lado, varios hechos indican que la repetición está culturalmente condicionada. Por ejemplo, su alcance varía ampliamente entre países, reflejando el grado de aceptación o rechazo de las sociedades hacia la medida (v.g., OECD 2010, 2016). También hay diferencias en las normativas nacionales que regulan la repetición (European Education and Culture Executive Agency, 2011) y en el modo en cómo los países manejan la diversidad del alumnado, lo cual parece asociado a la eficacia de la medida (Goos et al., 2021). Finalmente, los efectos de la repetición parecen depender de las medidas paliativas previstas: en algunos sistemas educativos la repetición no se acompaña de apoyos adicionales, mientras que en otros se prevén acciones complementarias, alternativas o programas especiales (Fernández-Alonso et al., 2022¸Valbuena et al., 2021). Todo ello justifica centrar el resto de la revisión teórica en el contexto español.

Comparada con la tradición anglosajona, la investigación española sobre repetición es muy reciente y, en gran parte, se desarrolla gracias a los datos liberados por las evaluaciones a gran escala nacionales (v.g., López-Agudo et al., 2024) e internacionales (v.g., Agasisti y Cordero, 2017; Blanco-Varela & Amoedo, 2025). Las conclusiones sobre la relación entre repetición y estatus social no parecen unánimes. Duran-Bonavila et al. (2024) encuentran que el estatus social pierde su capacidad para predecir la repetición cuando se controlan las habilidades cognitivas; y Fernández y Rodríguez (2008) señalan que el nivel socioeconómico deja de ser estadísticamente significativo al considerar los resultados en PISA. En línea similar, Carabaña (2011) afirma que la repetición no es una medida clasista, y que repetir se explica por lo que razonablemente cabría esperar: el desempeño escolar, medido también como las puntuaciones en PISA.

No obstante, la investigación española ha concluido mayoritariamente que existe una relación inversa entre las medidas de estatus social y la probabilidad de repetir (Arroyo et al., 2019; Cabrera et al, 2019; Carabaña, 2013, 2015; Choi et al., 2018; Cobreros & Gortazar, 2023; Cordero et al., 2014; García-Pérez et al., 2014; González-Betancor y López-Puig, 2016; López-Rupérez et al., 2021). Sin embargo, dentro de este grupo las estimaciones de la fuerza de la relación son variadas. Por ejemplo, Arroyo et al. (2019, p. 85) afirman que en la repetición “la preponderancia de las variables socioeconómicas no es clara”, y Carabaña (2015, p. 24) señala que “los determinantes sociales son mucho menos importantes” para explicar la repetición. En el extremo contrario, Cobreros & Gortazar (2023) y OECD (2016) concluyen que, a igualdad de competencias escolares el 25% del alumnado de menor nivel socioeconómico tiene casi cuatro veces más probabilidades de repetir que el 25% del alumnado de mayor nivel socioeconómico. Los datos de Choi et al., (2018) permiten estimar que la probabilidad de repetir de un estudiante situado en la mediana del cuarto inferior de estatus social es 4,4 veces mayor que la del alumnado ubicado en la mediana del cuarto superior. Los informes de fuentes oficiales, que generalmente contienen análisis descriptivos, ofrecen estimaciones aún más sombrías y compatibles con un sistema altamente reproductor de las desigualdades de acceso a la escuela (Instituto Vasco de Evaluación e Investigación Educativa [IVEI], 2009). El Alto Comisionado contra la Pobreza Infantil (2020) advierte que uno de cada dos estudiantes en hogares situados en el primer cuartil de renta repite durante la escolaridad obligatoria, mientras que en los hogares con más recursos esta cifra no llega a uno de cada diez; y la Consejería de Educación del Principado de Asturias (2016) concluye que el 60% de las repeticiones se concentran en el 30% del alumnado del estrato social bajo.

Esta variabilidad de resultados, que es muy poco útil para el diseño de las políticas educativas, podría explicarse, al menos en parte, por la calidad del diseño de los estudios: las investigaciones con escaso control sobre el sesgo de selección y el ajuste de covariables tienden a sobrestimar los efectos adversos de la repetición (Allen et al., 2009; Jackson, 1975; Lorence, 2006). En España, salvo excepciones (López-Agudo et al., 2024; Rodríguez-Rodríguez, 2022), la mayoría de la investigación sobre repetición está basada en diseños transversales (Choi et al., 2018) donde la principal variable independiente (por lo general los resultados en una prueba externa) se mide después de la dependiente (Carabaña, 2015). Ello puede contaminar las conclusiones, al ser imposible garantizar la equivalencia de los grupos (repetidores y promocionados) antes de repetir, introduciendo, por tanto, un sesgo de selección en las estimaciones.

El presente trabajo tiene como finalidad estimar las probabilidades de repetir de tres grupos de estatus sociocultural. Si bien, el objetivo no es original, nuestra investigación aporta una perspectiva novedosa en un doble sentido. En primer lugar, lo hará con una base de datos que cumple todas las características exigibles a una investigación de calidad sobre repetición (Goos et al., 2021; Valbuena et al., 2021): maneja una muestra representativa; dispone de un conjunto de covariables sustantivas medidas pre y post-repetición; y ejecuta un análisis de propensión para minimizar el sesgo de selección antes de repetir.

En segundo lugar, las precitadas características de la base de datos permiten plantear un objetivo adicional y novedoso en la literatura sobre repetición en España: mostrar cómo variaciones en el plan de análisis de unos mismos datos ofrecerán estimaciones diferentes sobre la magnitud de la relación repetición-estatus sociocultural. Para ello se compararán los resultados de tres modelos que se enuncian a continuación:

• Modelo 1: descriptivo. No incluye variables de control y reproduce las estimaciones de los informes oficiales (v.g., IVEI, 2009) y de los análisis de más baja calidad.
• Modelo 2: transversal. Recrea los resultados de la aproximación analítico-metodológica más habitual en la investigación española: análisis de regresión multivariada sobre un diseño descriptivo expost facto (v.g., Cobreros & Gortazar, 2023), con ajuste de covariables post-repetición.
• Modelo 3: longitudinal. Es el diseño de más calidad al incluir un doble control: ajuste de covariables post-repetición y equiparación de grupos ante-repetición para minimizar el sesgo de selección (Krestschmann et al., 2019).

Hasta donde alcanza nuestro conocimiento, no existe en España un trabajo que incluya el doble control ante-y post-repetición sobre una única muestra. A la vista de las evidencias previas (v.g., Allen et al., 2009) se espera que el modelo con menor control de sesgos muestre efectos mayores, es decir, que sobreestime la probabilidad de repetir del alumnado de estatus social bajo. Sin embargo, el arreglo con mejor control experimental ofrecerá efectos más moderados que, en ciertas condiciones, podrían llegar a diluir la significación estadística.

Método

La muestra inicial era de 7479 estudiantes que, en la práctica, conformaban la población escolar de 4º de Educación Primaria del Principado de Asturias en año académico 2008/09. Todo el alumnado fue evaluado en dos ocasiones, en 4º EP y 2º ESO, que en adelante denominaremos respectivamente T₁ y T₂. Para disponer de una muestra lo más homogénea posible, de la base original se eliminaron los siguientes casos: estudiantes sin información suficiente antes de T₁ (N = 100); quienes repitieron antes de T₁ (N = 677); quienes repitieron al finalizar 4º curso, es decir, seis semanas después de T₁ (N = 149); y quienes no participaron en T₂ por traslado entre T₁ y T₂ o por ausencia en T₂ (N = 554). La muestra final quedó compuesta por 5999 estudiantes nacidos en 1999, que en T₁ eran de la misma edad y curso. De ellos, 762 repetirán entre T₁ y T_2.

Instrumentos 

La información manejada proviene de tres fuentes: registros administrativos, pruebas cognitivas y cuestionarios de contexto para el alumnado.

Variable dependiente

Condición de repetición, variable binaria (1 = haber repetido entre T₁ y T₂) extraída de los registros administrativos de la Consejería de Educación del Principado de Asturias.

Variable de interés

Grupo-ISEC del alumnado. El profesorado respondió a una encuesta que registraba los estudios y profesiones de los progenitores de cada estudiante. Este modo de recabar la información es más fiable que los autoinformes del alumnado y apenas produce pérdida de datos. Con estos registros se construyó un Índice Socioeconómico y Cultural (ISEC) que, siguiendo el procedimiento establecido por Peña-Suárez et al. (2009), fue tipificado [N(0,1)]. El Análisis Factorial Exploratorio señaló que el ISEC es esencialmente unidimensional: la implementación óptima del Análisis Paralelo (Timmerman & Lorenzo-Seva, 2011) recomendó un único factor; el porcentaje de varianza explicada por el primer factor (61,41%) es elevado; y los índices de unidimensionalidad (UniCo = ,952; MIREAL = ,307) y ajuste del modelo (CFI = ,977; RMSR = .049) son muy buenos. A partir de la puntuación del ISEC individual se creó, por recodificación, la variable Grupo-ISEC que divide la muestra en terciles: ISECBajo, Medio y Alto.

Variables de ajuste

Se consideraron 8 variables sociodemográficas. Dos de nivel individual procedentes de los registros administrativos: género (1 = Mujer) y nacionalidad (1 = Emigrante). El resto son variables de centro medidas en T₁ y T₂: titularidad (1 = Centro público), proporción de emigrantes (yEmigraT1 e yEmigraT2), y promedio del ISEC (yZISEC_T1 e yZISEC_T2).

La trayectoria escolar y el rendimiento académico se definieron con 12 variables. La medida de trayectoria fue Cambio de centro entre T₁ y T₂, variable dicotómica (1 = Sí). El resto son medidas de rendimiento académico que incluyeron las Calificaciones Lengua española, Matemáticas e Inglés en T₁ y T₂, las cuales también se promediaron para obtener una Media General de Rendimiento (ZMGR_T1 y ZMGR_T2). Las ocho variables de calificaciones fueron estandarizadas a la escala N(0,1) y en el análisis multinivel centradas sobre la media del centro, para que valores positivos señalen rendimientos por encima de su centro. Finalmente, como medida de rendimiento cognitivo en T₁ se incluyeron las puntuaciones en la Evaluación de Diagnóstico Asturias 2009, que evaluó tres competencias: Comunicación en Lengua Inglesa, Aprender a Aprender y Competencia Social y Ciudadana (Test_ING, TestAaA y Test_SOC)1. Dichas puntuaciones se calcularon mediante modelos derivados de la Teoría de Respuesta al Ítem (logísticos unidimensionales de 2 y 3 parámetros) con el programa Parscale 4,1 (du Toit, 2003), y se expresaron en una escala N(500,100). A su vez las 11 variables de rendimiento académico se promediaron por centro, para disponer de un proxy del nivel medio del centro.

Finalmente, se consideraron dos variables socioemocionales: autoconcepto y esfuerzo académico. El alumnado respondió a un cuestionario de contexto que contenía cinco afirmaciones del tipo: “aprendo las lecciones fácilmente”. Cada afirmación fue valorada en una escala Likert de cuatro puntos: nunca o casi nunca; a veces; habitualmente; siempre o casi siempre. Con las respuestas se construyó la escala Autoconcepto académico (ZAutoCon_T1 y ZAutoCon_T2) que en T₁ es esencialmente unidimensional: el primer factor explica el 66,55 % de la varianza; la implementación óptima del análisis paralelo recomendó una única dimensión; y, tanto los índices de unidimensionalidad (UNICO = ,999, ECV = ,982, MIREAL = .090; Calderón-Garrido et al., 2019), como los de ajuste (CFI = ,999; RMSEA = .011; RMSR = .008) fueron excelentes. En T₂ los datos van en la misma línea. El primer factor explica el 72,84% de la varianza; el análisis paralelo sigue recomendando una única dimensión; y los indicadores de unidimensionalidad (UNICO = ,998, ECV = ,959, y MIREAL = ,155) y ajuste (CFI = ,996; RMSEA = .060; RMSR = .023) son buenos. Finalmente, pese al reducido número de ítems, la escala parece consistente en los dos momentos (T₁: α = ,87, ω = ,88; T₂: α = ,91; ω = ,91). Las puntuaciones ZAutoCon_T1 y ZAutoCon_T2 se expresaron en una escala normal [N(0,1)], donde valores positivos señalan buen autoconcepto académico.

Finalmente, la variable del esfuerzo académico (ZEsfuerzo_T1 y ZEsfuerzo_T2) se construyó a partir de las respuestas a cinco afirmaciones del tipo: “termino mis tareas aunque sean muy difíciles”. El grado de acuerdo con cada afirmación se valoró igual que con el autoconcepto. Pese a contener pocos ítems, la escala mostró alta consistencia interna (T₁: α = ,80, ω = ,80; T₂; α = ,77, ω = ,78). En T₁ el primer factor explica el 55,5% de la varianza total y muestra excelentes índices de ajuste (GFI = ,999, RMSR = .022; Calderón-Garrido et al., 2019). En T₂ las propiedades psicométricas son similares: el primer factor explica el 52,6% de la varianza y los índices de ajuste son muy buenos (GFI = ,998, RMSR = .029). Los pesos factoriales de todos los ítems oscilan entre ,523 and ,748, lo que confirma que la escala es esencialmente unidimensional en los dos momentos (Postigo et al., 2021a, b). Para el estudio de las evidencias de validez de la estructura interna y de la fiabilidad de las puntuaciones se empleó el programa FACTOR,12.04.04 (Ferrando & Lorenzo-Seva, 2017).

Procedimiento

El estudio es una explotación secundaria de la Evaluación de Diagnóstico Educativo del Principado de Asturias, un programa que fue regulado por la Consejería de Educación regional con el siguiente reparto de responsabilidades: los equipos directivos gestionaron la aplicación dentro de su centro; el Servicio de Inspección realizó el control de calidad del programa; y el Servicio de Evaluación codificó y analizó los datos.

Análisis de datos

Como se señaló, para mitigar los sesgos inherentes a todo estudio sobre repetición esta investigación implementa una estrategia de doble de control: la equiparación de puntuaciones y el ajuste de modelos multinivel.

Equiparación de puntuaciones en T₁

La equiparación de puntuaciones se realizó mediante un análisis de propensión (PSM, por la siglas en inglés: Propensity Score Matching), que es la aproximación más usada por la investigación psicoeducativa sobre repetición (Krestschmann et al., 2019; Wu et al., 2010). Su finalidad es emparejar un grupo experimental (repetidores) con un grupo control (promocionados) para sean equivalentes antes del tratamiento (repetición, Stuart, 2010; Zhao et al., 2021). El PSM sigue una serie de pasos (Ho et al., 2011) que aquí se resumen en tres etapas: planificación, ejecución y evaluación de los resultados.

Inicialmente se seleccionaron las siguientes variables de emparejamiento en T₁: (1) factores sociodemográficos: Mujer, Emigrante, Centro_Publico_T1 e yZISEC_T1; (2) proxis del rendimiento previo: calificaciones en Lengua, Matemáticas e Inglés en T₁, la media general de rendimiento (ZMGR_T1) y las puntuaciones en la Evaluación de Diagnóstico Asturias 2009; (3) medidas socioemocionales: ZAutoCon_T1 y ZEsfuerzo_T1. Todas las medidas actitudinales y de rendimiento, se consideraron a nivel individual y de centro. Por otro lado, las mujeres, en comparación con los hombres, muestran mejores desempeños en las áreas comunicativo-lingüísticas (Mullis et al., 2023) y suelen esforzarse más académicamente (Postigo et al., 2021a), aunque tienden a percibirse menos competentes, especialmente en matemáticas (Mejía-Rodríguez et al, 2021). Además, los centros públicos presentan desempeños escolares más bajos y mayor proporción de emigrantes y repetidores (Instituto Nacional de Evaluación Educativa, 2019). Por ello, el emparejamiento también incluyó las interacciones entre estas variables. En suma, las puntuaciones de propensión se estimaron mediante un modelo que contenía 27 covariables y 16 términos de interacción entre variables.

En la fase de ejecución los estudiantes de cada grupo se emparejan según sus puntuaciones de propensión, las cuales se expresan como la probabilidad condicional de recibir un tratamiento (v.g., repetir) dado el vector de covariables especificadas (Zhao et al., 2021). Existen diversos métodos de emparejamiento y la literatura recomienda comparar varios y elegir el que ofrezca mejor balance (Austin, 2014). En este caso se compararon dos tipos de algoritmos. Por un lado, métodos de emparejamiento de casos uno a uno: vecino más próximo sin reemplazo, emparejamiento óptimo por pares y emparejamiento genético. Por otro, los algoritmos que emplean pesos no uniformes: vecino más próximo con reemplazo, emparejamiento generalizado completo y subclasificación. Para mejorar el balance de las equiparaciones, y dependiendo de las posibilidades de cada método, se incluyeron customizaciones como el emparejamiento en un orden específico, el reemplazo de casos, restricción de las distancias entre pares o emparejamientos con k > 1.

Finalmente, .el método de emparejamiento se seleccionó en función de dos criterios: robustez del balance y alcance muestral. Nótese que cada criterio minimiza un tipo de sesgo que, en ocasiones, son contrapuestos: efecto del tratamiento y selección muestral. Mejor balance indica una adecuada equiparación y, por tanto, menor sesgo al estimar el efecto del tratamiento. Sin embargo, si para lograr una equiparación robusta deben imponerse fuertes restricciones (por ejemplo, emparejar solo los casos con diferencias muy pequeñas en sus puntuaciones de propensión) entonces aumenta la probabilidad de excluir casos del emparejamiento, lo que introduce el sesgo de selección muestral o por emparejamiento incompleto. En este estudio, se consideró balance satisfactorio cuando las diferencias estandarizadas entre los grupos y las diferencias en la función de distribución acumulada empírica (eCDF) eran cercanas a cero; y las ratios de varianza cercanas a uno. Por otro lado, el sesgo por emparejamiento incompleto se valoró según el porcentaje de casos descartados, no emparejados y el tamaño de la muestra efectiva lograda por cada algoritmo. El emparejamiento se realizó con el paquete Matching (Sekhon, 2011), y la evaluación del balance con Cobalt (Greifer, 2023), ambos en R (R Core Team, 2023).

Modelos multinivel en T2

Los fenómenos escolares son de naturaleza multinivel y, lógicamente, cada nivel de jerarquía tiene una variabilidad distinta y los errores no son independientes (Gaviria & Castro, 2005). Los modelos jerárquicos o multinivel están específicamente desarrollados para analizar datos que tienen estructura anidada y corrigen el problema del “efecto del diseño” en los casos donde los errores no son independientes (Fernández-Alonso & Muñiz, 2019). Por otro lado, dado que la variable dependiente es binaria no es realista asumir el supuesto de normalidad. Por ello, se empleó el modelo logístico binario multinivel (Bernouilli), que permite emplear variables predictoras de distinto tipo (continuas, discretas, binarias…) en todos los niveles de análisis.

Según lo señalado al final de la Introducción, en este estudio se ajustaron tres modelos. El modelo 1, que estima las probabilidades de repetir de cada grupo ISEC sin variables de control, tiene dos funciones: servir de comparación para el resto de modelos y recrear las estimaciones brutas del análisis descriptivo. El modelo 2 incluye las covariables sociodemográficas, escolares, cognitivas y socioemocionales medidas en T₂ y reproduce las estimaciones del diseño cross-sectional, mayoritario entre la investigación española sobre repetición. El modelo 3 añade al anterior las ponderaciones de la equiparación de grupos previa a la repetición y contiene, por tanto, un doble control estadístico: el ajuste de covariables post-repetición del diseño transversal y la equiparación de grupos ante-repetición (Krestschmann et al., 2019).

Los resultados de estos modelos se presentarán en términos odds (posibilidades) y odds ratios (OR). Estás últimas permiten comparar las odds de diferentes valores de una variable independiente, cuantificando y señalando el sentido de la asociación entre la variable dependiente y sus predictores en la regresión logística binaria. Los análisis se realizaron con HLM 7.0 (Raudenbush et al., 2011). 

Valores perdidos

El volumen de datos perdidos osciló, según la variable, entre 0% y 12% y se recuperaron en un procedimiento de dos etapas: cuando un caso tiene datos incompletos en una variable, los datos faltantes se reemplazaron por la media del sujeto. Para los valores completamente perdidos se empleó el algoritmo Expectation-Maximization con variables auxiliares que ofrece el programa SPSS 24 (IBM, 2016). Fernández-Alonso et al., (2012) mostraron que este procedimiento en dos etapas es el que mejor recupera los datos perdidos cuando, como es este caso, el tamaño de pérdida es pequeño y el sesgo moderado.

Resultados

Previo a presentar el resultado de los modelos ajustados es necesario ofrecer evidencias sobre la calidad del emparejamiento de los grupos en T₁. Es un punto básico para interpretar la comparación de los modelos posteriores, especialmente el resultado del modelo 3, donde se asume que la correlación entre repetición y los predictores en T₁ (ante repetición) es igual a 0.

Equiparación de los grupos en T₁

Los dos procedimientos de emparejamiento con mejor balance fueron: el vecino más próximo sin reemplazo (NN) entre los algoritmos de equiparación uno-a-uno y el emparejamiento generalizado completo (GFM) entre los algoritmos con pesos no-uniformes. Finalmente el eligió el GFM porque, a diferencia del NN, permite usar todos los casos del grupo de control, criterio preferible cuando, como era este caso, dos procedimientos ofrecen un balanceo similar (Sävje et al., 2021). La muestra equiparada quedó compuesta por 762 repetidores y 5237 no-repetidores que equivalen a una muestra de control efectiva de 395 casos.

El Gráfico I representa las diferencias de medias estandarizadas entre los grupos antes y después de la equiparación. Antes de la equiparación, la posición de los círculos advierte de diferencias altamente significativas que favorecen al grupo de promocionados: por ejemplo, la diferencia de las calificaciones escolares está en torno a 1,5 desviaciones típicas. Con este desequilibrio en T₁ será imposible dilucidar si las potenciales diferencias que se encuentren en T₂ son fruto de haber repetido o sólo reflejan la discrepancia inicial.

GRAFICO I. Diferencia de medias (puntos Z) entre los grupos antes y después de la equiparación.

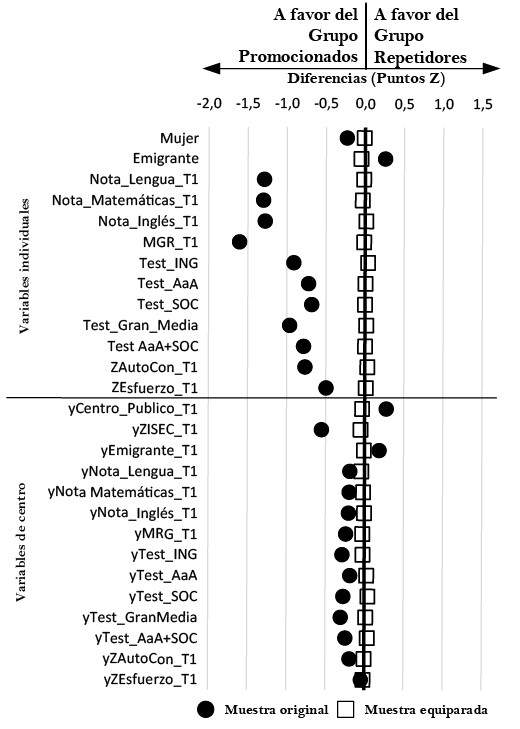
Nota. MGR = Media General de Rendimiento; ING = Inglés; AaA = Aprender a Aprender; SOC = Competencia Social y Ciudadana; AutoCon = Autoconcepto Académico; Esfuerzo = Esfuerzo Académico; ISEC = Índice Socioeconómico y Cultural.

Fuente: elaboración propia

Los cuadrados reflejan las diferencias después de la equiparación: todas ellas son inferiores a |0,1| y, por ello, los marcadores oscilan sobre el valor Z = 0. Así, el emparejamiento estadístico configuró dos grupos que antes de repetir eran comparables en cuanto a rendimiento previo, rasgos socio-emocionales y características sociodemográficas. Ello permite descartar que las diferencias que potencialmente se encuentren en T₂ estén relacionadas con las variables equiparadas en T₁, minimizando el sesgo de selección de los grupos a comparar.

Comparación de modelos

La Tabla I muestra los resultados del modelo descriptivo. El intercepto (-1,94) corresponde al logit del ISEC_Medio, el cual tiene asociada una probabilidad de repetir baja (OR = 0,14) y bastante precisa dado el estrecho margen del intervalo de confianza. Por su parte, la OR del grupo ISEC_Alto (0,17) señala una probabilidad de repetir aproximadamente un 85% más baja que en el grupo de referencia, mientras que el alumnado del grupo bajo tiene más del doble de posibilidades de repetir que el grupo medio y casi unas 13 veces más (2,11 / 0,17) que el grupo alto.

TABLA I. Modelo sin covariables de ajuste: predicción de repetir

La Tabla II recoge las estimaciones del modelo transversal. Al incluir las variables de control, la probabilidad de repetir en el grupo ISEC_Medio se reduce en casi dos tercios (OR = 0,06). La OR del grupo alto prácticamente se duplica (0,30), señalando que la probabilidad de repetir se reduce al 70%, mientras que en el grupo ISEC_Bajo la probabilidad de repetir es aproximadamente un 66% más alta que en el grupo de referencia y unas 5,5 veces superior al grupo ISEC_Alto.

TABLA II. Modelo transversal: predicción de repetir

En el modelo longitudinal (Tabla III) el principal cambio ocurre con el alumnado de ISEC_Bajo: el coeficiente queda en el límite de la significación estadística y su probabilidad de repetir es solo un 3% mayor que la del grupo ISEC_Medio. En la comparación entre los grupos extremos el efecto también se reduce drásticamente, prácticamente a la mitad: la OR del grupo ISEC_Bajo es ahora 2,4 veces mayor que la del ISEC_Alto. Algunas covariables en T₂ pierden su significación estadística por el efecto de la equiparación estadística en T₁.

TABLA III. Modelo longitudinal: predicción de repetir

El gráfico II representa una forma alternativa de comparar las estimaciones de los modelos. Muestra la probabilidad de repetir en cada grupo según el modelo. Se observa cómo el modelo longitudinal rebaja drásticamente las posibilidades de repetición de los grupos medio y bajo, manteniendo bastante estable la probabilidad del grupo más favorecido.

GRAFICO II. Probabilidad de repetir por modelo y grupo de ISEC

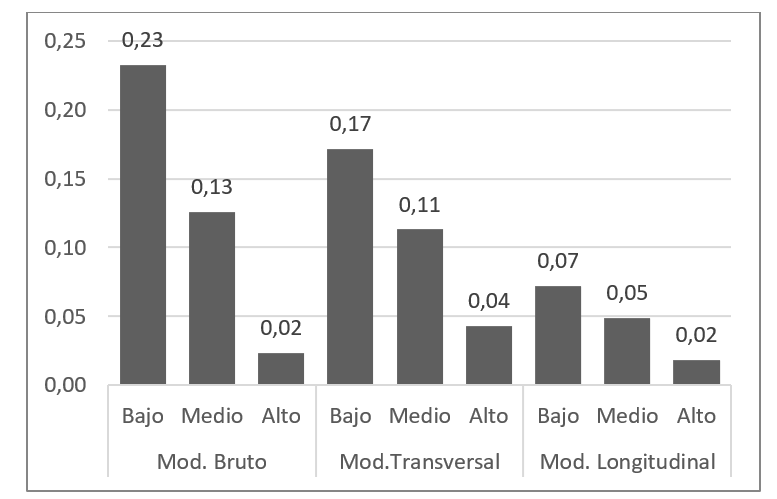
Fuente: elaboración propia

Discusión

Mayoritariamente, la investigación educativa ha identificado una asociación inversa entre los indicadores de estatus social y la probabilidad de repetir. No obstante, las conclusiones no son unánimes (v.g., Fernández & Rodríguez, 2008). Además, entre las investigaciones que encuentran relaciones significativas las estimaciones de la fuerza de la asociación son bastante variables (v.g., Carabaña, 2015; Cobreros & Gortazar, 2023). Una razón plausible de estas diferencias pudiera ser el diseño de los estudios, estando bien documentado que la falta de control de los sesgos tiende a sobrestimar los efectos negativos de la repetición (Lorence, 2006).

En este contexto, la presente investigación compara la probabilidad de repetir en función del estatus socioeconómico y cultural, ajustando sobre una misma base de datos tres modelos analíticos que simulan otros tantos diseños de investigación: (1) descriptivo, sin control de variables; (2) transversal, con control de covariables post-repetición; y (3) longitudinal, con doble control de sesgos ante- y post-repetición. Hasta donde alcanza nuestro conocimiento, se trata de un estudio inédito en la investigación española sobre la asociación repetición-estatus social. La comparación es posible porque se dispone de una base de datos de alta calidad que permite simular condiciones de análisis que incluyan paulatinamente mayores controles de los sesgos asociados a la repetición.

En coherencia con la mayor parte de la investigación previa (v.g., Choi et al., 2018; Cordero et al., 2014; García-Pérez et al., 2014; López-Rupérez et al., 2021) el estudio concluye que la repetición está afectada por la clase social. Esta evidencia también ha sido confirmada en estudios realizados en sistemas educativos muy diversos (v.g., Bastos & Ferrão, 2019; Ferrão et al., 2017; Klapproth & Schaltz, 2015; Salza, 2022; Xia & Kirby, 2009). Sin embargo, nuestros datos señalan que, al menos en el contexto español, la relación entre repetición y clase social debe ser matizada. Como era esperable en el modelo descriptivo el estatus socio-cultural tiene un fuerte impacto en la probabilidad de repetir. Los estudiantes de ISEC bajo enfrentan mayores probabilidades de repetir que su compañeros de ISEC medio, mientras que los estudiantes de ISEC alto están significativamente protegidos frente al riesgo de repetición. El modelo 2 reproduce las estimaciones de los análisis transversales, mayoritarios en la investigación española: todas las covariables en T₂ son significativas y, una vez controladas, la probabilidad de repetir del grupo ISEC_Bajo es 5,5 veces mayor que la del ISEC_Alto, un valor similar al estimado para Asturias con los datos de los dos últimos PISA (6,2 veces, Cobreros & Gortazar, 2023).

En el tercer modelo se producen algunos cambios interesantes que se resumen en tres conclusiones. En primer lugar, comparado con el modelo transversal, el modelo longitudinal reduce la disparidad en la probabilidad de repetir entre los grupos de ISEC extremos (bajo vs alto) en un 56%, pasando de 5,5 a 2,4 veces. Ello parece confirmar que un mayor control de sesgos produce estimaciones más conservadoras del efectos negativos de la repetición (Allen et al., 2009). Aunque en España hay trabajos que van más allá del ajuste de covariables en diseños descriptivos expost-facto (v.g., Rodríguez-Rodríguez, 2022), las evidencias ahora aportadas apuntan a la necesidad de desarrollar investigaciones que consideren todas las potenciales fuentes de sesgo en el estudio de la repetición (Goos et al., 2021; Valbuena et al., 2021).

En segundo lugar, se observó que, en el modelo longitudinal la diferencia en las OR de los grupos de ISEC medio y bajo prácticamente desaparece. Ello introduce una matización a las conclusiones previas sobre la relación entre repetición y clase social. Existe cierto consenso (v.g., Carabaña, 2015; García-Pérez et al., 2014) al señalar que la repetición tiende a concentrarse en los hijos de madres con pocos estudios o en la minoría cuyos progenitores presentan niveles de instrucción muy bajos. Los datos actuales apuntan a una interpretación alternativa ya que las clases medias y bajas muestran probabilidades de repetición similares. En el contexto español, donde repite un tercio de la población escolar, este hallazgo tampoco parece tan sorprendente: con semejante alcance tampoco cabría esperar que la clase media salga indemne. Por tanto, a la vista de las estimaciones del modelo longitudinal bien parece que lo más correcto sería decir que en España puede repetir el hijo de cualquiera, salvo que provenga de un hogar de estatus socio-cultural alto.

Por último, al margen del efecto del estatus social, el modelo longitudinal ha identificado dos variables personales altamente significativas en T₂: las calificaciones escolares y el esfuerzo académico, es decir, los dos criterios fundamentales empleados por los equipos docentes para proponer la medida de repetición. En ese sentido, el modelo ofrece una imagen coherente con lo esperado en el tema (Carabaña, 2011).

Las anteriores matizaciones no deben ocultar que la conclusión general de este trabajo es preocupante: en España, a igualdad de dificultades de aprendizaje, niveles de esfuerzo y otras características sociodemográficas, la clase social impacta diferencialmente en las propuestas de repetición de los equipos docentes. Ello invita a reflexionar sobre el contexto en que se toma la decisión y sus consecuencias sobre la equidad del sistema. La repetición está catalogada como una medida extraordinaria de atención a la diversidad. Sin embargo, un hecho que afecta al 30% no debiera considerarse tan extraordinario. Nuestras evidencias insisten en la necesidad de tomar la decisión con cautela para que no contribuya a incrementar las desigualdades de acceso y permanencia en el sistema educativo o, como señalan estos datos, para no reproducir la situación de privilegio de la minoría situada en el escalón más alto del estatus socio-cultural.

Finalmente, los datos de este estudio deben interpretarse a la luz de varias limitaciones. En primer lugar, las dos medidas están separadas por cuatro cursos. Disponer de una medida intermedia hubiera permitido tener mayor control de las trayectorias escolares: tal distancia entre las dos medidas ha podido introducir variaciones que afecten a los resultados (Kretschmann et al., 2019). Por otro lado, aunque el conjunto de variables de ajuste es bastante sustantivo, no se dispone de medidas específicas de habilidades cognitivas y de relaciones sociales y, por ello, no es posible saber cómo afectaría a los resultados contar con este tipo de variables que parecen modular la relación entre repetición y estatus social (Duran-Bonavila et al, 2024; Wu et al., 2010). Además, las medidas socioemocionales empleadas (autoconcepto y esfuerzo) fueron autoinformadas por el alumnado y todas las afirmaciones de los ítems estaban redactadas en sentido positivo. Por tanto, no puede descartarse que las puntuaciones socioemocionales empleadas incluyan sesgos de aquiescencia (Hernández-Dorado et al., 2025; Primi et al., 2019). Para superar estas limitaciones la investigación futura sobre repetición en España necesitará diseñar estudios específicos que incluyan el seguimiento de cohortes a lo largo de la escolarización y medidas repetidas pre- y post-repetición. Son necesarios, por tanto, diseños con muestras equiparadas o que alternativamente empleen algún enfoque cuasi-experimental (análisis de discontinuidad en la regresión, métodos basados en variables instrumentales o análisis de diferencias en diferencias) para controlar los sesgos y disponer de estimaciones ajustadas. Igualmente, convendría considerar un conjunto amplio de resultados educativos, más allá del rendimiento académico (v.g., esfuerzo, factores socio-afectivos y de ajuste social, etc.) y conectar la repetición con resultados a medio-largo plazo, tales como abandono educativo temprano de la educación y la formación o la incorporación al mercado de trabajo.

En países con alta tasa de repetición como España, impera la cultura de la repetición, es decir, la creencia socialmente compartida de que repetir es beneficioso (European Education and Culture Executive Agency, 2011). Sin embargo, la evidencia indica que esta práctica tiene un alto coste económico y social sin beneficios académicos claros (Goos et al., 2021). En todo caso, disponer de evidencias no cambia automáticamente las prácticas docentes (IVEI, 2009), por lo que se requieren medidas alternativas más equitativas y eficaces (Consejería de Educación del Principado de Asturias, 2016). Para alinear el sistema español con las tasas internacionales de repetición (v.g., OCDE, 2016) se proponen cinco estrategias, especialmente beneficiosas para el alumnado con mayor situación de vulnerabilidad (Fernández-Alonso et al, 2022). En primer lugar, adaptar la repetición al carácter excepcional que tiene en la normativa vigente, la cual ha eliminado el número fijo de materias suspensas como criterio de decisión automático y promueve decisiones colegiadas basadas en la relevancia de las asignaturas no superadas y las expectativas de recuperación y éxito en el curso siguiente. Igualmente es esencial reforzar la detección temprana de dificultades académicas mediante sistemas de alerta y apoyo individualizado, evitando que el bajo rendimiento derive en repetición, especialmente en educación secundaria, donde la medida carece de sentido preventivo en la mayoría de los casos. En tercer lugar, se recomienda el empleo de metodologías de enseñanza adaptadas a la diversidad, como la enseñanza diferenciada y el aprendizaje cooperativo, junto con la ampliación de programas de refuerzo educativo, tutorías especializadas y recursos extracurriculares. Por su parte, la formación docente debe priorizar la evaluación formativa y enseñanza inclusiva, para que la respuesta a la heterogeneidad no sea la repetición. Finalmente, sería necesario flexibilizar la estructura curricular y organizativa de los centros, permitiendo la personalización de los itinerarios educativos y la promoción adaptativa del alumnado.

Material suplementario

Este artículo dispone de material suplementario online donde se muestran los detalles del análisis PSM (comparación de los algoritmos de equiparación, evaluación del balance y ejemplos de script): https://osf.io/nq7c3/files/osfstorage

Referencias bibliográficas

Agasisti, T., & Cordero, J. M. (2016). The determinants of repetition rates in Europe: Early skills or subsequent parents’ help? Journal of Policy Modeling, 39(1), 129–146. https://doi.org/10.1016/j.jpolmod.2016.07.002

Allen, C. S., Chen, Q., Willson, V. L., & Hughes, J. N. (2009). Quality of research design moderates effects of grade retention on achievement: A meta-analytic, multi-level analysis. Educational Evaluation and Policy Analysis, 31(4), 480–499. https://doi.org/10.3102/0162373709352239

Alto Comisionado contra la Pobreza Infantil (2020). Pobreza infantil y desigualdad educativa en España. Autor.

Arroyo, D., Constante, I. A., & Asensio, I. (2019). La repetición de curso a debate: Un estudio empírico a partir de PISA 2015. Educación XX1, 22(2), 69–92. https://doi.org10.5944/educXX1.22479

Austin, P. C. (2014). A comparison of 12 algorithms for matching on the propensity score. Statistics in Medicine, 33, 1057–1069. https://doi.org/10.1002/sim.6004

Ayres, L. P. (1909). Laggards in our schools. Charities Publication Committee.

Bastos, A., & Ferrão, M. E. (2019). Analysis of grade repetition through multilevel models: A study from Portugal. Cadernos de Pesquisa, 49, 270–288. https://doi.org/10.1590/198053146131

Biegler, C. D., & Green, V. P. (1993). Grade retention: A current issue. Early Child Development and Care, 84, 117–122. https://doi.org/10.1080/0300443930840111

Blanco-Varela, B., & Amoedo, J. M. (2025). Efectos de la repetición escolar según el perfil socioeconómico del estudiante. Revista de Educación, (407), 257–288. https://doi.org/10.4438/1988-592X-RE-2025-407-658

Cabrera, L., Pérez, C., Santana, F. & Betancort, M. (2019). Desafección escolar del alumnado repetidor de segundo curso de Enseñanza Secundaria Obligatoria. International Journal of Sociology of Education, 8(2), 173–203. https://doi.org/10.17583/rise.2019.4139

Calderón-Garrido, C., Navarro-González, D., Lorenzo-Seva, U., & Ferrando, P. J. (2019). Multidimensional or essentially unidimensional? A multi-faceted factor-analytic approach for assessing the dimensionality of tests and items. Psicothema, 31(4), 450–457. https://doi.org/10.7334/psicothema2019.153

Carabaña, J. (2011). Las puntuaciones PISA predicen casi toda la repetición de curso a los 15 años en España. Revista de Sociología de la Educación-RASE, 4(3), 283–303.

Carabaña, J. (2013). Repetición de curso y puntuaciones PISA ¿cuál causa cuál? En Ministerio de Educación, Cultura y Deporte (Ed.), PISA 2012. Programa para la Evaluación Internacional de los Alumnos. Informe Español (Vol. II, pp. 32-66). Autor.

Carabaña, J. (2015). Repetir hasta 4º de Primaria: determinantes cognitivos y sociales según PIRLS. Revista de Sociología de la Educación-RASE, 8(1), 7–27.

Choi, Á., Gil, M., Mediavilla, M., & Valbuena, J. (2018). Predictors and effects of grade repetition. Revista de Economía Mundial, 48, 21–42. https://doi.org10.33776/rem.v0i48.3882

Cobreros, L, & Gortazar, L. (2023). Todo lo que debes saber de PISA 2022 sobre equidad. EsadeEcPol – Save The Children.

Consejería de Educación del Principado de Asturias (2016). La repetición escolar: hechos y creencias. Informes de Evaluación, 2.

Cordero, J. M., Manchón, C., & Simancas, R. (2014). La repetición de curso y sus factores condicionantes en España. Revista de Educación, 365, 13–37. https://doi.org/10.4438/1988-592X-RE-2014-365-263

du Toit, M. (2003). IRT from SSI: BILOG-MG, MULTILOG, PARSCALE, TESTFACT. Scientific Software International.

Duran-Bonavila, S., Rodríguez-Gómez, A., & Becerril-Galindo, M. (2024). Determinants of grade repetition in Spain. Analysis of cognitive and socio-economic, mediated by ethnic factors. International Journal of Educational Psychology, 13(1), 63–85. https://doi.org/10.17583/ijep.12804

European Education and Culture Executive Agency. (2011). Grade retention during compulsory education in Europe. Regulations and statistics. European Commission Publications Office. https://data.europa.eu/doi/10.2797/50570

Fernández, J. J., & Rodríguez, J. C. (2008). Los orígenes del fracaso escolar en España: Un estudio empírico. Mediterráneo económico, 14, 323–349.

Fernández-Alonso, R., Suárez-Álvarez, J., & Muñiz, J. (2012). Imputación de datos perdidos en las evaluaciones diagnósticas educativas [Imputation methods for missing data in educational diagnostic evaluation]. Psicothema, 24(1), 167–175. https://psycnet.apa.org/record/2012-02525-026

Fernández-Alonso, R., & Muñiz, J. (2019). Calidad de los sistemas educativos: modelos de evaluación. Propósitos y Representaciones, 7(spe), e347–347. http://dx.doi.org/10.20511/pyr2019.v7nSPE.347

Fernández-Alonso, R., Postigo, Á., García-Crespo, F. J., Govorova, E., & Ferrer, Á. (2022). Repetir no es aprender. Mitos desmentidos y alternativas posibles a una práctica ineficiente e inequitativa. Save the Children.

Ferrando, P. J., & Lorenzo-Seva, U. (2017). Program FACTOR at 10: Origins, development and future directions. Psicothema, 29(2), 236–240. https://doi.org/10.7334/psicothema2016.304

Ferrão, M. E., Costa, P. M., & Matos, D. A. S. (2017). The relevance of the school socioeconomic composition and school proportion of repeaters on grade repetition in Brazil: A multilevel logistic model of PISA 2012. Large-scale Assessments in Education, 5, 1–13. https://doi.org/10.1186/s40536-017-0036-8

García-Pérez, J. I., Hidalgo-Hidalgo, M., & Robles-Zurita, J. A. (2014). Does grade retention affect students’ achievement? Some evidence from Spain. Applied Economics, 46(12), 1373–1392. https://doi.org/10.1080/00036846.2013.872761

Gaviria, J. L., & Castro, M. (2005). Modelos jerárquicos lineales. La Muralla.

González-Betancor, S. M., & López-Puig, A. J. (2016). Grade retention in primary education is associated with quarter of birth and socioeconomic status. PloS one, 11(11), Article e0166431. https://doi.org/10.1371/journal.pone.0166431

Goodlad, J. I. (1954). Some effects of promotion and non-promotion upon the social and personal adjustment of children. The Journal of Experimental Education, 22(4), 301–328. http://dx.doi.org/10.1080/00220973.1954.11010490

Goos, M., Pipa, J., & Peixoto, F. (2021). Effectiveness of grade retention: A systematic review and meta-analysis. Educational Research Review, 34, 1–14. https://doi.org10.1016/j.edurev.2021.100401

Greifer, N. (2023). cobalt: Covariate Balance Tables and Plots. R package version 4.5.1

Heffernan. H., Gilbertson, E., Greenblatt, E., & Hills, J. A. (1952). What research says about nonpromotion. California Journal of Elementary School, XXI(1), 7–28.

Hernández-Dorado, A., Ferrando, P. J., & Vigil-Colet, A. (2025). The impact and consequences of correcting for acquiescence when correlated residuals are present. Psicothema, 37(1), 11–20. https://doi.org/10.70478/psicothema.2025.37.02

Ho, D. E., Imai, K., King, G., & Stuart, E. A. (2011). MatchIt: Nonparametric Preprocessing for Parametric Causal Inference. Journal of Statistical Software, 42(8), 1–28. https://doi.org/10.18637/jss.v042.i08

Holmes, C. T. (1989). Grade level retention effects: A meta-analysis of research studies. In L. A. Shepard, & M. L. Smith (Eds.), Flunking Grades: Research and Policies on Retention (pp. 16–33). The Flamer Press.

Holmes, C. T., & Matthews, K. M. (1984). The effects of nonpromotion on elementary and junior high school pupils: A meta-analysis. Review of Educational Research, 54(2), 225–236. https://doi.org/10.2307/1170303

Hong, G., & Yu, B. (2008). Effects of kindergarten retention on children´s social-emotional development: an application of propensity score method to multivariate, multilevel data. Developmental Psychology, 44(2), 407–421. https://doi.org/10.1037/0012-1649.44.2.407

Hunt, C. S., & Seiver, M. (2017). Social class matters: Class identities and discourses in educational contexts. Educational Review, 70(3), 342–357. https://doi.org10.1080/00131911.2017.1316240

Instituto Nacional de Evaluación Educativa (2019). PISA 2018 - Programa para la Evaluación Internacional de los Estudiantes. Informe español. Ministerio de Educación y Formación Profesional.

Instituto Vasco de Evaluación e Investigación Educativa (IVEI). (2009) Efecto de las repeticiones de curso en el proceso de enseñanza-aprendizaje del alumnado. Gobierno Vasco.

Jackson, G. B. (1975). The research evidence on the effects of grade retention. Review of Educational Research, 45(4), 613–635. https://doi.org/10.2307/1170067

Jimerson, S. R. (2001a). Meta-analysis of grade retention research: Implications for practice in the 21st century. School Psychology Review, 30(3), 420–437. http://dx.doi.org/10.1080/02796015.2001.12086124

Jimerson, S. R. (2001b). A synthesis of grade retention research: Looking backward and moving forward. California School Psychologist, 6, 47–59. https://doi.org/10.1007/BF03340883

Klapproth, F., & Schaltz, P. (2015). Who is retained in school, and when? Survival analysis of predictors of grade retention in Luxembourgish secondary school. European Journal of Psychology of Education, 30, 119–136. https://doi.org/10.1007/s10212-014-0232-7

Kretschmann, J., Vock, M., Lüdtke, O., Jansen, M., & Gronostaj, A. (2019). Effects of grade retention on students’ motivation: A longitudinal study over 3 years of secondary school. Journal of Educational Psychology, 111, 1432–1446. http://dx.doi.org/10.1037/edu0000353

López-Agudo, L.A., Latorre, C.P. & Marcenaro-Gutierrez, O.D. (2024). Grade retention in Spain: The right way? Educational Assessment, Evaluation and Accountability, 36, 53–74. https://doi.org/10.1007/s11092-023-09421-6

López-Rupérez, F., García-García, I., & Expósito-Casas, E. (2021). La repetición de curso y la graduación en Educación Secundaria Obligatoria en España. Análisis empíricos y recomendaciones políticas. Revista de Educación, 394, 325–353. https://doi.org10.4438/1988-592X-RE-2021-394-510

Lorence, J. (2006). Retention and academic achievement research revisited from a United States perspective. International Education Journal, 7(5), 731–777.

Mejía-Rodríguez, A. M., Luyten, H., & Meelissen, M. R. (2021). Gender differences in mathematics self-concept across the world: An exploration of student and parent data of TIMSS 2015. International Journal of Science and Mathematics Education, 19(6), 1229–1250.

Méndez, I., & Cerezo, F. (2018). La repetición escolar en Educación Secundaria y factores de riesgo asociados. Educación XXI, 21(1), 41–62. https://doi.org/10.5944/educxx1.20172

Michavila, F., & Narejos, A. (2021). Algunas debilidades del sistema educativo español. Ministerio de Educación y Formación Profesional.

Mullis, I. V. S., von Davier, M., Foy, P., Fishbein, B., Reynolds, K. A., & Wry, E. (2023). PIRLS 2021 International Results in Reading. Boston College, TIMSS & PIRLS International Study Center. https://doi.org/10.6017/lse.tpisc.tr2103.kb5342

OECD (2010). PISA 2009 Results (Volume I): What students know and can do – student performance in reading, mathematics and science. OECD Publishing. https://doi.org/10.1787/9789264091450-en

OECD (2016). PISA 2015 Results (Volume I): Excellence and Equity in Education. OECD Publishing. https://doi.org/10.1787/9789264266490-en

Peña-Suárez, E., Fernández-Alonso, R., & Fernández, J. M. (2009). Estimación del valor añadido de los centros escolares. Aula Abierta, 37(1), 3–18.

Postigo, Á., Cuesta, M., Fernández-Alonso, R., García-Cueto, E., & Muñiz, J. (2021a). Academic grit modulates school performance evolution over time: A latent transition analysis. Revista de Psicodidáctica, 26(2), 87–95. https://doi.org/10.1016/j.psicoe.2021.03.001

Postigo, Á., Cuesta, M., Fernández-Alonso, R., García-Cueto, E., & Muñiz, J. (2021b). Temporal stability of grit and school performance in adolescents: A longitudinal perspective. Psicología Educativa, 27(1), 77–84. https://doi.org/10.5093/psed2021a4

Primi, R., Santos, D., De Fruyt, F., & John, O. P. (2019). Comparison of classical and modern methods for measuring and correcting for acquiescence. British Journal of Mathematical and Statistical Psychology, 72(3), 447–465. https://doi.org/10.1111/bmsp.12168

R Core Team (2023). R: A language and environment for statistical computing. R Foundation for Statistical Computing. https://www.R-project.org/

Raudenbush, S. W., Bryk, A. S., Cheong, Y. F., Congdon, R. T., & Du Toit, M. (2011). HLM7 Hierarchical Linear and Nonlinear Modeling. Scientific Software International.

Rodríguez-Rodríguez, D. (2022). Grade Retention, Academic Performance and Motivational Variables in Compulsory Secondary Education: A Longitudinal Study. Psicothema, 34(3), 429–436. https://doi.org/10.7334/psicothema2021.582

Salza, G. (2022). Equally performing, unfairly evaluated: The social determinants of grade repetition in Italian high schools. Research in Social Stratification and Mobility, 77, Article e100676. https://doi.org/10.1016/j.rssm.2022.100676

Sävje, F., Higgins, M., & Sekhon, J. (2021). Generalized Full Matching. Political Analysis, 29(4), 423–447. https://doi.org/10.1017/pan.2020.32

Sekhon, J. S. (2011). Multivariate and propensity score matching software with automated balance optimization: The matching package for R. Journal of Statistical Software, 42(1), 1–52. https://doi.org/10.18637/jss.v042.i07

Shepard, L. A., & Smith, M. L. (1989). Flunking grades: Research and policies on retention. The Falmer Press.

Shepard, L. A., & Smith, M. L. (1990). Synthesis of research on grade retention. Educational Leadership, 47(8), 84–88.

Stuart, E. A. (2010). Matching methods for causal inference: A review and a look forward. Statistical Science, 25(1), 1–21. https://doi.org/10.1214/09-STS313

Timmerman, M. E., & Lorenzo-Seva, U. (2011). Dimensionality assessment of ordered polytomous items with Parallel Analysis. Psychological Methods, 16(2), 209–220. https://doi.org/10.1037/a0023353-

Urbano, A., & Álvarez, L. (2019). La repetición de curso en la adolescencia: Influencia de variables sociofamiliares. HEKADEMOS, 27, 51–59.

Valbuena, J., Mediavilla, M., Choi, Á., & Gil, M. (2021). Effects of Grade Retention Policies: A Literature Review of Empirical Studies Applying Causal Inference. Journal of Economic Surveys, 35(2), 408–451. https://doi.org10.1111/joes.12406

Wu, W., West, S. G., & Hughes, J. N. (2010). Effect of grade retention in first grade on psychosocial outcomes. Journal of Educational Psychology, 102, 135–152. http://doi.org/10.1037/a0016664

Xia, N., & Kirby, S. N. (2009). Retaining students in grade: A literature review of the effects of retention on students’ academic and nonacademic outcomes. RAND Technical Report.

Zhao, Q. Y., Luo, J. C., Su, Y., Zhang, Y. J., Tu, G. W., & Luo, Z. (2021). Propensity score matching with R: conventional methods and new features. Annals of Translational Medicine, 9(9), 812. http://dx.doi.org/10.21037/atm-20-3998

Información de contacto / Contact info: Laura M. Cañamero. Universidad de Oviedo, Facultad de Psicología, Departamento de Psicología. E-mail: lauramcanamero@uniovi.es