¿Qué pasó en España con PISA 2018? Una explicación a partir de los tiempos de respuesta a los ítems

What happened with PISA 2018 in Spain? An explanation based on response times to items

https://doi.org/10.4438/1988-592X-RE-2025-411-727

José G. Clavel

Universidad de Murcia

https://orcid.org/0000-0001-5800-319X

Francisco Javier García-Crespo

Universidad Complutense de Madrid

https://orcid.org/0000-0002-1050-462Y

Luis Sanz San Miguel

Instituto Nacional de Evaluación Educativa (INEE)

https://orcid.org/0000-0002-1050-462X

Resumen

Palabras clave:

PISA 2018, fluidez lectora, rapid guessing, process data, comportamientos anómalos, modelo loglinear, rendimiento en lectura

Abstract

Keywords:

Introducción

El 19 de noviembre de 2019, la OCDE emitió una nota oficial adelantando que los datos de lectura para España no se harían públicos con los datos del resto de países el 3 de diciembre de 2019. En el comunicado decían:

“Spain’s data met PISA Technical Standards with no apparent technical errors or manipulations identified. However, the data show implausible student-response behaviour. Consequently, the OECD is unable to assure full international comparability of Spain’s results at this moment. Spain has agreed to follow the OECD’s recommendation to defer the publication of its results and data while possible sources of those anomalies are investigated”.

Meses más tarde, el 23 de julio de 2020 se hacían públicos los datos de lectura, con un breve estudio independiente dando una posible explicación al hecho a partir de las fechas de realización de la prueba PISA, entre otras razones. En ese mismo documento, llamado Annex A9, se apuntaba que quizás el efecto de una parte de la prueba, los Reading Fluency, podrían tener más importancia de la prevista:

“The analysis of Spain’s data also reveals how the inclusion of reading fluency items may have strengthened the relationship between test performance and student effort in PISA more generally. The OECD is therefore exploring changes to the administration and scoring of reading fluency items to limit the occurrence of disengaged response behaviour and mitigate its consequence”.

Aparentemente, por tanto, el comportamiento anómalo de algunos estudiantes en los Reading Fluency (RF en adelante) fue lo que desencadenó los resultados inesperados en algunas CCAA, y que ocasionó la suspensión de la publicación, en diciembre de 2019, de los resultados de lectura PISA 2018, de España. Pero… ¿Qué características tienen los estudiantes que tuvieron ese comportamiento anómalo? ¿Por qué en unas CCAA hubo ese problema, y en otras no? ¿Qué pudo provocar este comportamiento? A estas preguntas trataremos de responder en el siguiente estudio empleando los resultados de lectura de PISA 2018, finalmente publicados para España.

Se encuadra nuestro trabajo entre aquellos que analizan los datos disponibles desde que las pruebas se realizan, como en el caso de PISA 2018, en una tableta (Goldhammer et al. 2020). En efecto, hacer los exámenes por ordenador (computer-based assessments) ha tenido varias consecuencias metodológicas. Entre otras, ha permitido diseñar pruebas adaptativas, que cambian según las respuestas de los estudiantes (como ocurre en las pruebas PISA); ha permitido diseñar ítems de respuesta que antes no eran técnicamente posibles, y sobre todo, ha permitido afinar en la evaluación de las pruebas, al incorporar toda esa información colateral al modelo (ver por ejemplo Bezirhan et al., 2020) ahora disponible. Dentro de esta tercera área está nuestro trabajo: usamos la traza informática (log-files) que genera el estudiante según avanza en la prueba (process data) para combinarla con lo que ha contestado (response data). Para una revisión de cómo se están integrando las dos fuentes de información en las LSAs como PISA puede consultarse Anghel et al (2024).

Dependiendo de la prueba, los mencionados log-files pueden incluir, para cada ítem y para cada persona, desde qué teclas pulsó, o el desplazamiento del cursor por la pantalla, hasta en evaluaciones más sofisticadas, el movimiento de los ojos o las pulsaciones cardiacas. En PISA 2018, los log-files recogían los tiempos de respuesta: unos tiempos excesivamente breves serían una indicación de rapid guessing behavior al contestar (Wise, 2017), que manifestaría lo que la OECD define como test-taker disengagement (Avvisati et al, 2024) y que es un riesgo posible en pruebas como PISA, donde los estudiantes, no se juegan nada (lo que la literatura denomina un low-stakes context).

Una segunda fuente de información disponible en PISA 2018 es la no-respuesta a ciertos ítems. Como señalan (Weeks et al. 2016), que un estudiante no responda no necesariamente significa que no sepa: puede ser que no haya llegado por falta de tiempo, o que simplemente no sé esforzó suficientemente. Sería otro aspecto, por tanto del test-taker disengagement. Sin embargo, como lo que pasó en España con PISA 2018 está relacionado con los RF, y estos fueron contestados por todos los participantes, dejaremos este aspecto de los logfiles para posteriores investigaciones.

Continuando con la introducción nos extenderemos en describir la estructura de la prueba, con especial mención por su importancia en nuestro trabajo de los RF. En la sección correspondiente a la metodología, presentaremos las variables seleccionadas para el estudio, un estudio descriptivo de los comportamientos anómalos por CCAA, y finalmente el modelo multinivel, log lineal, que explica qué factores están detrás de esos comportamientos anómalos. Los resultados de las estimaciones y una predicción de lo que hubiera pasado si los RF hubieran tenido otra ponderación se presentan en la sección siguiente. El trabajo termina con unas conclusiones y algunas recomendaciones que podrían evitar que lo que pasó en España con PISA 2018, se repita.

La estructura de la prueba: el diseño adaptativo multietapa

El hecho de poder realizar la evaluación PISA por ordenador permite implementar el proceso evaluativo mediante un diseño adaptativo multietapa (MSAT, MultiStage Adaptive Testing), que va presentando nuevos ítems al estudiante, según la habilidad que éste muestra hasta ese momento en el examen. Se logra así conocer con mayor precisión qué saben hacer con lo que saben los estudiantes en sus diferentes rangos de habilidad, consiguiendo una prueba más sensible, especialmente en los niveles más bajos de rendimiento de PISA.

El diseño MSAT para PISA 2018 constaba de tres etapas: core, stage1 y stage2. En cada una de estas etapas hay un cierto número de unidades (5 en el core, 24 en stage1 y 16 en stage2) cada una de ellas a su vez conteniendo varios ítems. En el dispositivo móvil en el que hace la prueba, al estudiante se le presenta una selección de estas unidades. En concreto, del total de 45 unidades y 245 ítems disponibles, cada estudiante se enfrentó a 7 unidades con un total de entre 33 y 40 ítems, en función de la habilidad mostrada al ir contestando. Una explicación detallada puede encontrarse en el Capítulo 2 del informe técnico de la prueba (OECD, 2018 https://www.oecd.org/pisa/data/pisa2018technicalreport/).

Además de esas tres etapas core, stage1 y stage2, PISA2018 incluyó una etapa previa para medir la fluidez lectora (RF) de los estudiantes. En esta etapa previa cada estudiante leía una expresión y luego indicaba si era lógica o no. Estos reading fluency items eran frases sencillas en las que los estudiantes únicamente tenían que indicar si tenía o no tenía sentido la expresión. Un ejemplo de frase sin sentido sería: “la ventana cantó la canción en voz alta”. Un ejemplo de frase que sí tiene sentido sería: “el hombre condujo el coche hasta el almacén”. Ambos ejemplos han sido extraídos de la prueba PISA 2018.En resumen, el estudiante empezaba la prueba con unos ítems RF extremadamente sencillos, seguía con una etapa principal aleatoria (core) y dos etapas posteriores (stage1 y stage2) que dependía de cómo fueran contestando la prueba: a partir del core, la asignación de los ítems ya está influenciada por el desempeño de los estudiantes en los ítems de puntuación automática realizados. Recordemos que, por la teoría de respuesta al ítem (IRT), la función estimada de rendimientos para cada alumno depende, no sólo de cómo contestó, sino también de cómo eran de difíciles las preguntas que acertó. Por tanto, un buen estudiante, al que sólo le preguntan cuestiones sencillas a las que responde correctamente, obtendrá una función estimada peor que un buen estudiante que ha respondido bien preguntas difíciles.

La medida de la fluidez en lectura

Como ya se ha señalado, la fluidez lectora (RF) de los estudiantes se midió en una etapa previa. Los resultados de esta etapa previa no influyen en qué ítems se incluyen en el cuadernillo (testlet) del estudiante. Respecto a su repercusión en la medida del rendimiento, la OCDE decidió no incluir los resultados de los RF en la medida de las diferentes subescalas en las que se descompone la lectura (location of information; understanding; evaluating and reflecting) pero sí incluirlos en la medida final del rendimiento en la competencia. No hemos encontrado publicada por la OCDE cómo han repercutido exactamente, pero a cambio, la OCDE proporciona, previa petición, los valores plausibles alternativos para cada estudiante, si no se hubiera tenido en cuenta el resultado del estudiante en los RF.

A partir de esos datos alternativos proporcionados por la OCDE, hemos obtenido los rendimientos medios por región y comparado con los resultados publicados, considerados los RF. Como se observa en la Figura 1 es evidente que en las CCAA de Cantabria, Madrid, Navarra, La Rioja y País Vasco, el efecto de los RF ha sido muy significativo, y distinto al patrón del resto de regiones, donde los resultados son más parecidos entre sí.

Figura 1

Rendimientos medios en Lectura en PISA 2018 por regiones, según se incluya o no en la calificación final el efecto de los reading fluency (RF)

Nota: Los valores numéricos están en la Tabla AI del Anexo.

Hay bastante información en la base de datos de PISA 2018 para cada uno de los ítems que miden la fluidez lectora, RF. La mayoría de los estudiantes se encontraron con 22 ítems. Para cada uno de ellos sabemos la respuesta, el tiempo que tardó en contestar, y si acertó o no en su respuesta. El número medio de aciertos para España fue de 19,33, con una mediana de 20 aciertos. Lo que se esperaba por otra parte, dada la sencillez de la prueba.

Sin embargo, al analizar los tiempos de respuesta, el total de tiempo empleado por el estudiante en responder a las 22 preguntas que se le presentaban, apareció un hecho extraordinario: una proporción no despreciable de alumnos (hasta un 15% en algunas CCAA) habían empleado menos de 22 segundos en responder a las 22 preguntas, lo que es demasiado poco tiempo. De hecho, esto era posible gracias a que los 22 ítems aparecían en la tableta consecutivamente y la respuesta, que era “sí” o “no”, se mostraba en sendos recuadros, siempre en la misma posición en pantalla. Bastaba con pulsar repetidamente en el cuadro con la respuesta para completar esta parte en menos de 22 segundos, acertando alrededor de la mitad de las preguntas. En la Figura 2 puede apreciarse, de nuevo, un comportamiento anómalo en los tiempos de respuesta de las Comunidades Autónomas de Madrid, Navarra, Rioja y País Vasco.

Figura 2

Distribución del tiempo empleado en responder a las 22 preguntas del RF en las distintas regiones.

Nota: La línea roja discontinua marca los 22 segundos

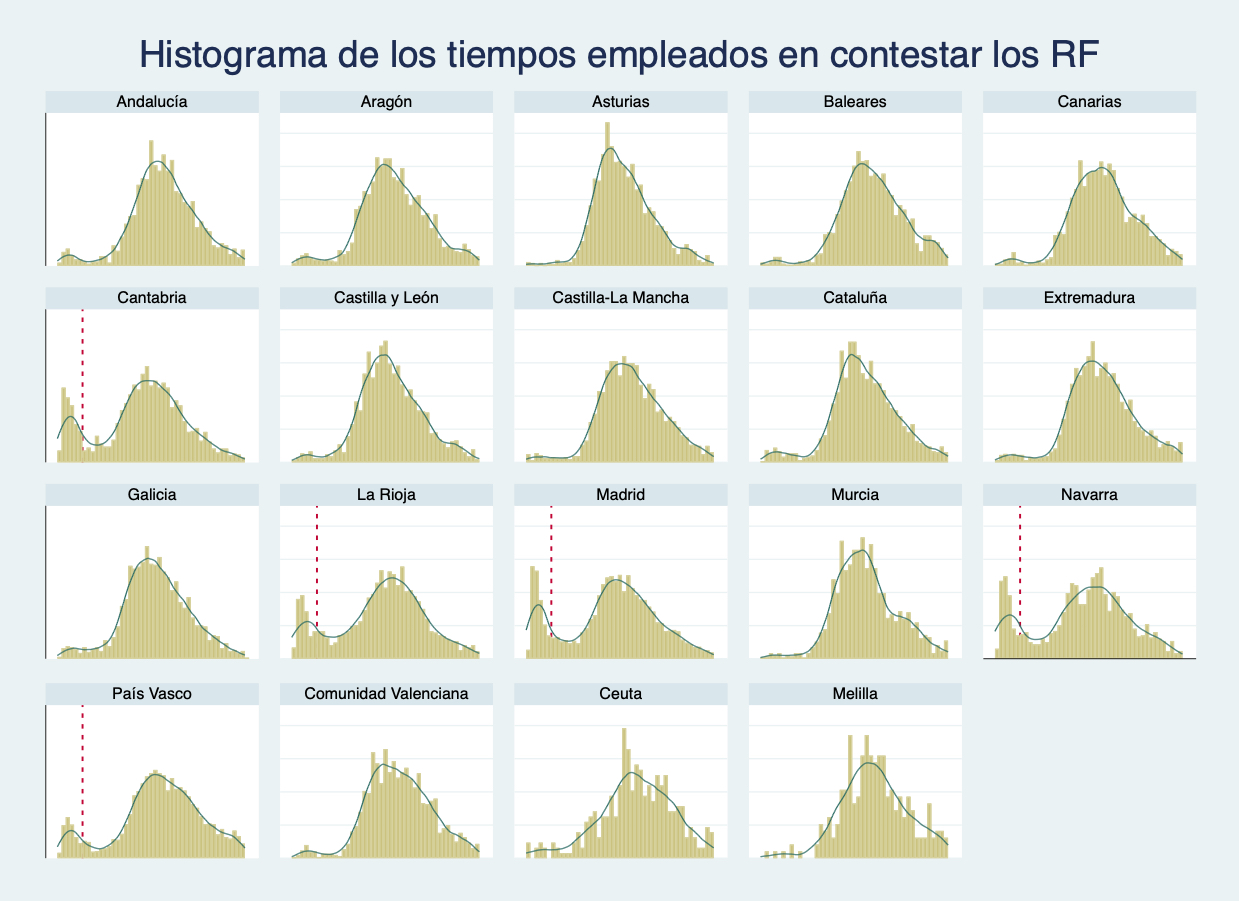
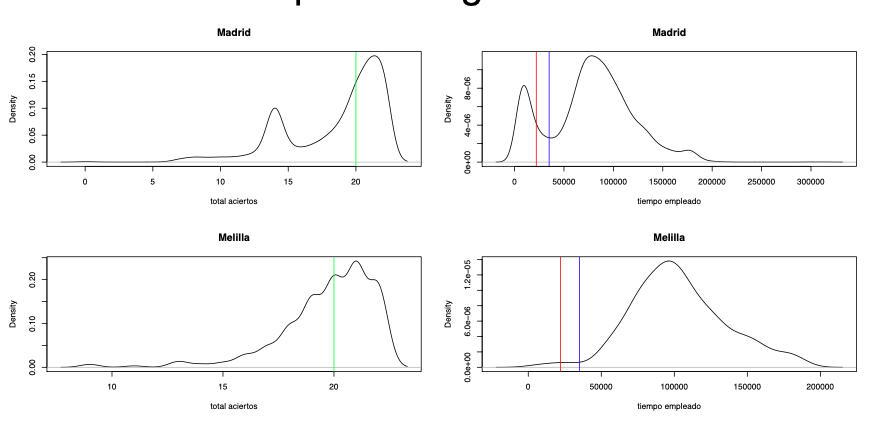
Fue ese patrón de tiempos de respuesta lo que nos dio la pista de lo que podría haber pasado. Comprobamos que la distribución en el número de aciertos de los ítems que medían la RF también estaba afectada por la misma anomalía, como refleja la Figura 3 que recoge la distribución de ambas variables para Madrid y Melilla. Era evidente por tanto que un grupo de estudiantes, relevante en algunas CCAA, había contestado los RF de modo “a la ligera”. Ahora quedaba determinar las características de los estudiantes que se comportaron así y, sobre todo, qué repercusión, si la hubiera, tenían en los resultados globales en lectura de la prueba.

Figura 3

Distribución del número de respuestas acertadas (izquierda) y los tiempos de respuesta (derecha) a las preguntas del RF para Madrid y Melilla en PISA 2018

Nota: La línea roja marca los 22 segundos; la azul los 35 segundos. El tiempo está medido en milisegundos.

Fuente: Elaboración propia a partir de los datos de PISA2018

Método

Lo primero que hicimos fue describir qué comportamientos eran anómalos. Para eso, estudiamos los tiempos de respuesta de los RF, relacionándolo con el desempeño a la lo largo de la prueba. A continuación, vimos cómo se distribuían estos estudiantes por CCAA, y sus características. Finalmente, con un modelo logit, estudiamos qué podría haber desencadenado el comportamiento anómalo de estos estudiantes.

Variable dependiente: el comportamiento anómalo

El comportamiento anómalo se da cuando un estudiante responde mal a los RF pero muy bien al resto de la prueba. Hay por tanto que definir que consideramos “responder mal” en la etapa previa, y “responder muy bien” en el resto de la prueba. Para la primera parte, calculamos la variable “puntuación obtenida en los RF” como:

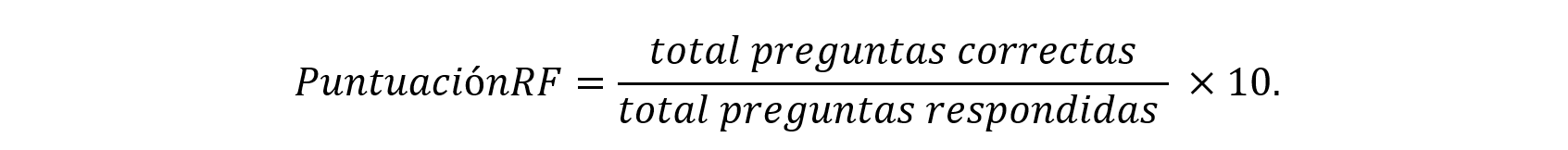
A partir de ella, en este trabajo hemos decidido que un estudiante respondió mal en la etapa previa del test cuando obtuvo una puntuación inferior a 8 sobre 10 en los RF. La distribución por regiones de los estudiantes, ponderados y sin ponderar, que obtuvieron puntuación inferior a 8 en RF se muestra en la Tabla 1. Alrededor del 28% de estos estudiantes pertenecen a centros educativos de la Comunidad de Madrid, el 18% son de centros de Andalucía y el 11% de Catalunya; País Vasco y Comunidad Valenciana presentan en torno al 6-7% y del resto de regiones los porcentajes son inferiores al 5%.

Tabla 1

Distribución por regiones de estudiantes con puntuación inferior a 8 en RF.

Evidentemente, una puntuación inferior a 8 en los ítems del RF también podría significar que el estudiante tiene dificultades de lectura. Por eso, el criterio para señalar un comportamiento anómalo es una combinación de cómo contestaron los RF, y el comportamiento en la siguiente fase de la prueba, el core. En concreto, distinguimos entre los estudiantes que tuvieron un mal inicio y “consistentemente” luego fueron clasificados en los niveles bajo y medio en el core y los de comportamiento “inconsistente”: los que se repusieron del mal inicio en los RF y obtuvieron un nivel alto en la etapa siguiente. Estos últimos representan el 16,66% (s.e.: 0,845) de los estudiantes que obtuvieron menos de un 8 en los RF y son los que señalamos como anómalos: buenos estudiantes que respondieron muy mal a los sencillos RF.

En la Tabla 2 se recoge, por comunidades autónomas (regiones), la proporción de estudiantes que habiendo obtenido puntuación inferior a 8 en la parte de RF, sin embargo, alcanzaron un nivel alto de rendimiento en el core. Galicia, País Vasco, Castilla y León, La Rioja, Navarra, Madrid y Cantabria, muestran los porcentajes más elevados, entre el 20% y el 30%, de esos estudiantes que estamos llamando de comportamiento anómalo.

Tabla 2

Porcentaje de estudiantes de “comportamiento anómalo” en cada región

Fuente: elaboración propia

Variables independientes

Para tratar de caracterizar a los estudiantes con comportamientos anómalos, hemos seleccionado diversas variables independientes, tanto a nivel estudiante como a nivel centro, que pasamos a describir en este apartado. Se presentan agrupadas según su naturaleza. Las variables categóricas están en la Tabla 3 y las continuas en la Tabla 4. La población objetivo del estudio son los estudiantes que obtuvieron una puntuación en los RF inferior a 8 puntos independientemente de su desempeño posterior. Para las variables cualitativas se recoge el porcentaje de cada categoría; para las variables continuas se presenta la media y la desviación típica y sus errores estándar respectivos. Debe tenerse en cuenta que estas últimas tienen media cero y desviación típica 1 para el conjunto de estudiantes evaluados en PISA 2018.

Tabla 3

Análisis de Variables Categóricas.

Nota: Porcentaje estimado de estudiantes en cada categoría, junto con el error estándar de la estimación entre los estudiantes que han obtenido puntuación inferior a 8 sobre 10 en el RF.

Fuente: Elaboración propia

Como se observa en la Tabla 3, de los estudiantes con puntuación inferior a 8 en RF, el 71,84% estaban matriculados en centros de titularidad pública, y, de estos, el 14,3% obtuvo un rendimiento de nivel alto en el CORE; mientras que esa cifra llegó al 23,0% de los estudiantes matriculados en centros de titularidad privada. Además, el 41,4% de los estudiantes con puntuación inferior a 8 en RF pertenecían a centros que adelantaron al mes de junio la evaluación extraordinaria, de los cuales alrededor del 23,6% obtuvo un nivel alto en el CORE; mientras que esa proporción es prácticamente la mitad entre los estudiantes de los centros que no adelantaron a junio dicha evaluación.

En el conjunto de estudiantes con puntuación inferior a 8 en RF, el 39,51% eran chicas y, de ellas, aproximadamente el 21,8% consiguieron llegar al nivel alto en el CORE, mientras que solo el 13,3% de los chicos alcanzó dicho nivel. De otra parte, en torno al 16,5% de estudiantes con menos de 8 puntos en RF tenían antecedentes de inmigración (1ª o 2ª generación) y de estos, alrededor del 9,2% llegó al nivel alto del CORE, por más del doble en el caso de los estudiantes nativos (19%) (Tabla 3).

Finalmente, entre los estudiantes con puntuación inferior a 8 en RF, el 41,6% ha repetido al menos un curso y de estos, solo un 3,8% obtuvo puntuación de nivel alto en el CORE, mientras que esa cifra llegó al 26,1% de los estudiantes que no han repetido curso (Tabla 3). En resumen, más de 7 de cada 10 estudiantes que tuvieron puntuación inferior a 8 en RF pertenecen a centros de titularidad pública, alrededor del 60% son chicos y la gran mayoría son nativos (83,5%). Además, debe observarse que 6 de cada 10 de estos estudiantes pertenecen a centros educativos de comunidades autónomas que adelantaron a junio del curso 2017-18 los exámenes extraordinarios, que habitualmente se celebraban en septiembre.

En la Tabla 4 están recogidas las estadísticas básicas para los estudiantes con una puntuación en los RF menor de 8 de las variables continuas del modelo. Hay dos que tienen que ver con los centros: Week que hace referencia a la semana en que se realizó la prueba en ese centro, y COLT que mide la implicación del profesorado en la prueba de lectura. Todas las variables están estandarizadas para tener media cero y desviación típica igual a uno en el conjunto de estudiantes participantes en PISA 2018.

Tabla 4

Análisis de variables continuas.

Nota: Media y desviación típica estimada de las estimaciones entre los estudiantes que han obtenido puntuación inferior a 8 sobre 10 en el RF.

Fuente: Elaboración propia

La media de la variable Week toma un valor alto positivo, lo que indica que una buena parte de los estudiantes incluidos en este análisis pasó las pruebas PISA de la mitad de la ventana de aplicación hacia delante, con lo que coincidirían en buena medida con las pruebas finales de su curso académico y esta coincidencia es más acusada en aquellos centros de comunidades que adelantaron a junio las pruebas de la evaluación extraordinaria. En cuanto a la colaboración del profesorado en la prueba de lectura (COLT), su valor negativo (-0,1380) indica un nivel bajo de colaboración de los docentes con la prueba PISA 2018.

En el conjunto de estudiantes objetivo de este trabajo, el esfuerzo realizado para responder a las pruebas (EFFORT), el apoyo del profesorado en las clases de lengua (TEACHSUP), la percepción de la propia dificultad para la lectura (SCREADFIFF), el uso de las TIC en las clases relacionadas con la materia (ICTCLASS) y la información proporcionada por el centro educativo sobre el mercado laboral (INFOJOB1) quedan muy próximas al valor cero, de modo que no parecen ser, para este conjunto de alumnado, aspectos que influyan por encima ni por debajo de la media general.

Aquellos que acertaron menos de 8 ítems en la parte de RF, muestran valores significativamente por encima de la media general en los aspectos relacionados con sentido de la vida (EUDMO), el clima escolar discriminatorio (DISCRIM) y el uso de las TIC tanto para actividades de trabajo escolar fuera del centro (HOMESCH) como para interacción social (SOIAICT). Por el contrario, estos estudiantes se declaran significativamente por debajo de la media general en lo que se refiere a su autoeficacia en cuestiones globales (GCSELFEFF) así como su experiencia en ser acosados (BEGBULLIED). Y aún son más negativas su percepción de la competencia propia en lectura (SCREACOMP), su percepción del clima disciplinario en sus clases de lengua (test language lessons) (DISCLIMA) y el nivel socioeconómico de su familia (ESCS) (Tabla IV).

Modelos log lineal

Terminamos la Sección metodológica del trabajo presentando el modelo que hemos empleado para caracterizar a los estudiantes con comportamiento “anómalo” en la prueba. Dada la estructura jerárquica de los datos y la naturaleza de la variable dependiente, el mejor recurso es un modelo multinivel log lineal. En efecto, como en otras oleadas de PISA, la selección de estudiantes que realizaron la prueba sigue un muestreo clásico de dos etapas (centros-alumnos) por conglomerados. En concreto, el modelo usado fue el bietápico estratificado secuencial por conglomerados (OCDE, 2017). Una vez determinado qué estratos representan mejor la población objetivo de cada estudio (Comunidad Autónoma y titularidad, el caso de España), dentro de cada uno, el procedimiento secuencial de selección de muestra comprende dos etapas. Una primera etapa de muestreo donde se seleccionan los centros secuencialmente y de manera proporcional a su tamaño (el tamaño del centro viene determinado por el número de estudiantes objetivo matriculados en el mismo). Por tanto, la probabilidad de que un centro sea seleccionado es proporcional a su tamaño (centros grandes tienen más probabilidad de ser seleccionados que centros pequeños). En la segunda etapa de muestreo se seleccionaron 42 alumnos que cumplían 16 años durante el curso de aplicación de la prueba independientemente de la clase o el curso en el que estuvieran matriculados. Si un centro seleccionado tenía 42 o menos alumnos objetivo matriculados, todos hacían la prueba.

Como hemos ya señalado, el modelo que mejor se ajusta a la estructura de muestreo y datos de este trabajo es el modelo de regresión logística multinivel (Cohen, Cohen, West, & Aiken, 2013; Gelman & Hill, 2006; Merino Noé, 2017; Snijders & Bosker, 2012), que modelizan adecuadamente la variabilidad de los datos en los diseños muestrales de las evaluaciones educativas internacionales a gran escala (De la Cruz, 2008; Iñiguez-Berrozpe & Marcaletti, 2018), al tiempo que evitan el uso de las ponderaciones replicadas presentes en las bases de datos (Fishbein, Foy, & Yin, 2021).

Por todo ello, para analizar el impacto de las variables predictoras sobre la condición de estudiante con comportamiento anómalo se han utilizado modelos logísticos multinivel de efectos fijos que recogen la estructura anidada de la muestra. Para la estimación de los modelos construidos para este trabajo se ha utilizado el software HLM6© utilizando la aproximación de Laplace para la estimación del modelo de Bernoulli (Raudenbush & Bryk, 2002) que permite llevar a cabo análisis utilizando variables dependientes binarias y niveles jerárquicos.

Las ecuaciones del modelo usado son:

Nivel 1 del modelo:

Nivel 2 del modelo:

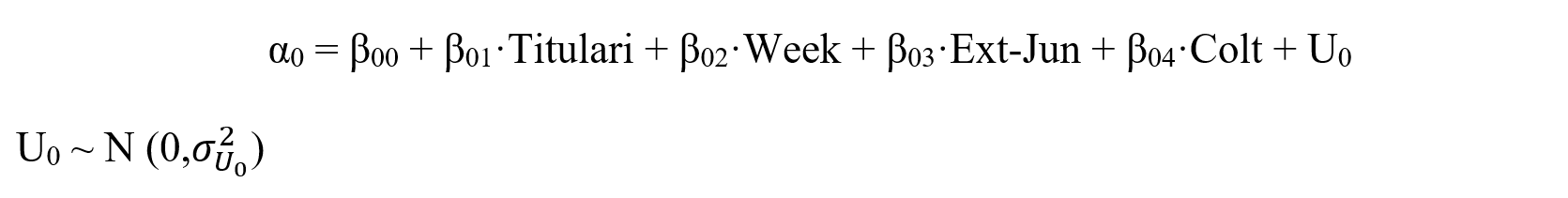
Donde,

Y, representa la condición o no de alumnado con comportamiento anómalo.

α_i, son los coeficientes fijos para cada variable predictora del nivel 1.

β_0i, son los coeficientes fijos para cada variable predictora del nivel 2.

β₀₀, es el intercepto de la regresión.

Las variables están ya presentadas en las Tablas III y IV.

Resultados

La Tabla 5 recoge los resultados del modelo jerárquico logístico, en el que la variable dependiente era la condición “comportamiento anómalo”. El modelo jerárquico construido consta de dos niveles: nivel de centro y nivel de alumnado. Se han observado variables altamente significativas en ambos niveles. En el nivel de centro cabe destacar que ni la titularidad del centro (TITULARI), ni el apoyo colaborativo del profesorado de lengua (COLT_MEA) tienen relevancia significativa sobre la probabilidad de que el alumnado esté considerado como de comportamiento anómalo. Lo que deja patente que el comportamiento anómalo en las respuestas del estudiante no se debe a características particulares del centro educativo. Sin embargo, sí es estadísticamente significativa la semana en la que el centro educativo realizó la prueba PISA (WEEK) (incremento de 10 puntos porcentuales para el alumnado que realizó la prueba en semanas más tardías) y aún en mayor medida resulta significativo que la Comunidad Autónoma haya adelantado a junio los exámenes extraordinarios (EXT_JUN), aumentando en 87 puntos porcentuales la probabilidad de alumnado de comportamiento anómalo en los centros de dicha Comunidad Autónoma. Variables íntimamente relacionadas, cuanto más tarde se realizó la prueba PISA en el centro educativo más probabilidad tenía de coincidir con el fin de curso y como consecuencia con la evaluación final de sus estudios en secundaria. No cabe duda que son variables exógenas al alumnado, pero sí que les provocaron un cierto grado de desgana o desmotivación hacia la prueba PISA. Pues, como decíamos antes, se vieron abocados a realizar una prueba externa al centro y a sus estudios conducentes al bachillerato durante el proceso de evaluación final de sus estudios secundarios.

Cómo y en qué medida afectaron estas variables de centro al comportamiento individual del estudiante se analizan considerando a nivel de alumnado del modelo multinivel ajustado, ni su sexo (SEXO), ya que afectó a chicas y chicos en igual medida o al menos no en proporciones estadísticamente diferentes, ni si consideraban tener apoyo educativo de su profesorado (TEACHSUP), como ya vimos en la variable del centro asociada al profesorado de lengua, tuvieron significación estadística en las estimaciones realizadas. No obstante, un considerable número de otras variables sí presentaron esta significación, cabe destacar las variables que midieron la repetición (REPETICI), la condición de inmigrante (INMIGRAN) y el clima discriminante del centro (DISCRIM). Un alumno o alumna repetidor tiene 80 puntos porcentuales menos de probabilidad de tener un comportamiento anómalo, siendo 30 puntos porcentuales menos de probabilidad en el caso del alumnado inmigrante y llega a disminuir hasta 25 puntos porcentuales la probabilidad de tener un comportamiento anómalo cuando el clima escolar es muy discriminatorio.

Es destacable que aquel alumnado que tenía más posibilidades de titular en 4º de ESO tuvo más probabilidad de considerarse de comportamiento anómalo, probablemente por el poco interés que puso al realizar la prueba PISA por su interferencia con sus estudios “principales”. Un estudiante que tiene un alto autoconcepto en la competencia lectora (SCREADCO) puede llegar a tener 38 % más de probabilidad de ser considerado raro. Adicionalmente, entre 15 y 20 puntos porcentuales significativos de probabilidad se encuentran las estimaciones de un gran número de variables, siendo las más relevantes el esfuerzo realizado por el alumnado (EFFORT: +19 puntos), el Índice Social Económico y Cultural (ESCS: + 18 puntos), el clima escolar positivo (DISCLIMA: +17 puntos) o la autoeficacia en la respuesta a aspectos globales (GCSELFEF: + 20 puntos). Variables estas que se consideran de carácter positivo en cuanto a sus antecedentes contextuales, pero de alguna manera marcan a un alumnado que no realizó la prueba con el interés o la motivación adecuada.

Entre las variables que disminuyen la probabilidad de ser identificado como estudiante anómalo son las que miden la percepción de dificultad en la competencia lectora (SCREADDI: -13 puntos) o el uso de las ICT fuera del ámbito escolar (SOIAICT: -9 % Puntos?).

Tanto la variable que mide la percepción de la dificultad en competencia lectora como el uso de ICT fuera del ámbito escolar están alineadas con las que medían incrementos porcentuales positivos en la probabilidad de considerarse al alumno o la alumna con un comportamiento anómalo. Debemos considerar que estas dos variables suelen medir rendimientos menores en el alumnado con carácter general y, por tanto, valores positivos en ellas hacen esperar más desmotivación hacia la competencia lectora con carácter general y más aún en las circunstancias que se desarrolló PISA en el ciclo 2018 y que se ha venido estudiando a lo largo de todo este artículo.

Tabla 5

Resultados del análisis multinivel

Fuente: Elaboración propia

Conclusiones

La exclusión, en diciembre de 2019, de los resultados de España en la prueba de lectura de PISA 2018 fue una decisión prudente por parte de la OCDE, después de observar unos rendimientos inesperadamente bajos en algunas Comunidades Autónomas. No toda la caída en el rendimiento en lectura es achacable a la naturaleza y estructura de la prueba, pero en este trabajo se ha demostrado que sí tuvo influencia significativa en algunos casos.

En concreto, la presencia de una parte inicial, los RF, que algunos estudiantes contestaron “como si no contara para la nota final”, repercutió negativamente en los rendimientos medios de ciertas Comunidades Autónomas ya que el diseño adaptativo multietapa de la prueba, y la obtención de los rendimientos personales a partir de la Teoría de Respuesta al Ítem, impide a los buenos estudiantes recuperar un mal comienzo.

La proporción de estudiantes que respondió “a la ligera” a los ítems de RF, empleando tiempos anormalmente cortos, no supera en la mayoría de las regiones el 5%, en el País Vasco y la Comunitat Valenciana se quedan ligeramente por debajo del 7% y es muy alta particularmente en tres regiones: Cataluña (11,09%), Andalucía (17,7%) y la Comunidad de Madrid (28,32%)

A los estudiantes que, realizando mal la parte de los RF, contestan muy bien en la etapa siguiente de la prueba (CORE) los hemos definido como de comportamiento anómalo. En siete regiones, la proporción de estudiantes que respondieron a la ligera en los RF pero alcanzaron un nivel alto en el CORE es elevada, cerca o por encima del 20%: Cantabria, Castilla y León, La Rioja, Comunidad de Madrid, Comunidad Foral de Navarra, País Vasco y Galicia (Tabla II). Un modelo logístico multinivel ha permitido descartar la titularidad del centro, el sexo de los estudiantes o el apoyo por parte del profesorado de lengua como factores relevantes para que el estudiante tenga un comportamiento anómalo. Por el contrario, que la prueba se realizara en las últimas semanas del curso (segunda ventana de aplicación), o que la Comunidad Autónoma haya adelantado a junio los exámenes extraordinarios, sí influyo de manera significativa a que el estudiante no tomara en serio la parte de los RF. A nivel estudiante, que la prueba le haya supuesto más esfuerzo y que el estudiante piense que es buen lector también hace más probable que tenga un comportamiento anómalo.

Por tanto, esos buenos estudiantes que tuvieron un comportamiento anómalo en la prueba de lectura de PISA 2018, que por diferentes razones respondieron de manera aleatoria -como indican sus tiempos de respuesta- a la parte de los RF: quizás les dijeron que no contaban, quizás entendieron que eran ejemplos para calibrar la tableta, quizás pensaron que no podría ser tan fácil la prueba… Pero, por el diseño de la prueba, ya no consiguieron rendir como sería esperable.

La OCDE ya manifestó que exploraría cambios en la administración y la repercusión de esos RF en el rendimiento final de los jóvenes, pero hasta que no vuelva a ser la lectura la competencia principal evaluada no podremos saberlo. Mientras, podría ser interesante estudiar en qué más países hubo un comportamiento anómalo de ciertos estudiantes, y qué características tenían estos. Es poco realista pensar que sólo en España se haya dado este fenómeno.

Finalmente, dada la transcendencia que los resultados de las evaluaciones internacionales a gran escala, como es PISA, tienen en la opinión pública y en las posibles mejoras de los programas educativos, consideramos que es importante resaltar cuáles son las principales causas que se han manifestado como relevantes de este aparente comportamiento anómalo en un porcentaje importante de estudiantes. A este respecto recomendamos:

• Modificación de la estructura de la prueba, de modo que incluya los RF pero no permita responder de modo automático. Por ejemplo, cambiando la presentación de cada uno de los ítems para que las posibles elecciones no aparezcan en el mismo sitio.

• Adelantar la realización de la prueba, de tal manera que se lleve a cabo los suficientemente lejos del final de curso y los estudiantes no estén preocupados con dicho final y puedan dedicarle más atención.

• Campaña de concienciación del alumnado sobre la importancia de la prueba, haciendo hincapié en la relevancia de la misma tanto a nivel nacional (comparación entre regiones) como internacional (comparación entre países).

Anexo

Para valorar la repercusión que ese comportamiento tuvo en el rendimiento medio final del estudiante contamos con los datos que la propia OCDE proporciona, a demanda, de los rendimientos en lectura sin contar la parte de los RF. Es decir, después de solicitarlo en la OCDE, contamos con una puntuación alternativa, diez valores plausibles alternativos en concreto, para medir el efecto medio de los RF.

En la Tabla AI está recogido el valor medio para cada Región incluyendo la parte de los RF (por tanto, los valores ya publicados por la OCDE en su informe de 23 de Julio de 2020), el valor medio de los rendimientos sin tener en cuenta la parte de los RF, y la diferencia entre uno y otro resultado.

TABLA AI. Rendimientos medios por Regiones, con y sin RF y tamaños muestrales. Diferencias en el rendimiento medio presentados en el Gráfico I.

Leyenda

• pv_read_mean: valor medio de los rendimientos en lectura de la Comunidad Autónoma publicados por la OCDE. (incluidos los RF?) ¿Este es el pv_readalt_mean?
• pv_read_mean: valor medio de los rendimientos en lectura de la Comunidad Autónoma sin considerar los resultados en los RF. Datos disponibles, a demanda, en la OCDE.
• pv_read_N: tamaño muestral.
• difere: diferencia entre los valores medios según se incluyan o no los RF. pv_readalt_mean – pv_read_mean

Referencias bibliográficas

Anghel, E., Khorramdel, L. and von Davier, M. (2024). The use of process data in large-scale assessments: a literature review. Large-scale Assess Educ 12, 13. https://doi.org/10.1186/s40536-024-00202-1

Avvisati, F. et al. (2024), “Item characteristics and test-taker disengagement in PISA”, OECD Education Working Papers, No. 312, OECD Publishing, Paris, https://doi.org/10.1787/7abea67b-en

Bezirhan, U., von Davier, M., and Grabovsky, I. (2020). Modeling Item Revisit Behavior: The Hierarchical Speed–Accuracy–Revisits Model. Educational and Psychological Measurement, 81(2), 363-387. https://doi.org/10.1177/0013164420950556

Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2013). Applied multiple regression/correlation analysis for the behavioral sciences. New York: Routledge.

De la Cruz, F. (2008). Modelos multinivel. Epidemiol, 12(3), 1-8. Obtenido de http://sisbib.unmsm.edu.pe/bvrevistas/epidemiologia/v12_n3/pdf/a02v12n3.pdf

Fishbein, B., Foy, P., & Yin, L. (2021). TIMSS 2019 User Guide for the International Database. Boston College, TIMSS & PIRLS International Study Center. Retrieved from timssandpirls.bc.edu/timss2019/international-database/

Gelman, A., & Hill, J. (2006). Data analysis using regression and multilevel/hierarchical models. Cambridge: Cambridge University Press.

Goldhammer F, Scherer R and Greiff S (2020) Editorial: Advancements in Technology-Based Assessment: Emerging Item Formats, Test Designs, and Data Sources. Front. Psychol. 10:3047. doi: 10.3389/fpsyg.2019.03047

Iñiguez-Berrozpe, T., & Marcaletti, F. (2018). Modelos lineales multinivel en SPSS y su aplicación en investigación educativa [Linear multilevel models in SPSS and its application in educational research]. REIRE Revista d’Innovació i Recerca en Educació, 11(1), 26-40. doi:10.1344/reire2018.11.118984

Merino Noé, J. (2017). La potencialidad de la Regresión Logística Multinivel. Una propuesta de aplicación en el análisis del estado de salud percibido. Revista de Metodología de Ciencias Sociales, 36, 177-211. doi:empiria.36.2017.17865

OCDE. (2017). PISA 2015 Technical Report. Retrieved from www.oecd.org/pisa/data/2015-technical-report/

Raudenbush, S. W., & Bryk, A. S. (2002). Hierarchical Linear Models: Applications and data analysis methods. Thousand Oaks: Sage Publications, Inc.

Snijders, T. A., & Bosker, R. J. (2012). Multilevel analysis: An introduction to basic and advanced multilevel modeling. London: Sage.

Weeks, J., von Davier M. and Yamamoto K. (2016): Using response time data to inform the coding of omitted responses. Psychological Test and Assessment Modeling, Volume 58, (4), 671-701

Wise, S.L. (2017), Rapid-Guessing Behavior: Its Identification, Interpretation, and Implications. Educational Measurement: Issues and Practice, 36: 52-61. https://doi.org/10.1111/emip.12165