Cognitive demand in Mathematics assessment criteria of the Galician curriculum: teaching implications

Demanda cognitiva en criterios de evaluación de Matemáticas del currículo de Galicia: implicaciones docentes

https://doi.org/10.4438/1988-592X-RE-2025-409-699

Laia Francina Tugores Blanco

Universidade de Vigo

https://orcid.org/0000-0001-7679-7683

Manuela Raposo-Rivas

Universidade de Vigo

https://orcid.org/0000-0001-7781-7818

Olalla García Fuentes

Universidade de Vigo

https://orcid.org/0000-0001-9084-0078

Abstract

Keywords:

cognitive processes, assessment criteria, curriculum, mathematics, Secondary Education

Resumen

Palabras clave:

Introduction

Cognitive processes are "the procedures carried out by human beings to acquire knowledge, in which very diverse faculties are involved, such as intelligence, attention, memory, and language, which may operate either consciously or unconsciously" (Suárez, 2016, p. 5). Regarding those involved in learning, the American psychologist and pedagogue Benjamin Bloom publishes, in the mid-20th century (1956), a taxonomy bearing his name, based on two types of thinking skills: lower-order thinking skills (LOST), namely knowledge, comprehension, and application, and higher-order thinking skills (HOST), which include analysis, synthesis, and evaluation. Subsequently, Anderson and Krathwohl (2001) revise this taxonomy, structuring the cognitive dimension into six major categories, expressed in the infinitive form to emphasize their dynamic nature. Arranged from lower to higher levels of complexity, these categories are remember, understand, apply, analyze, evaluate, and create. Abbreviated as RBT (Revised Bloom’s Taxonomy), each category represents objectives to be achieved as learning outcomes. Such authors conceptualize these processes as follows: remembering involves retrieving information; understanding consists of explaining ideas or concepts; applying means using information in another familiar situation; analyzing entails breaking information into components to explore insights and relationships; evaluating involves justifying a decision or course of action; and creating is based on generating new ideas, products, or perspectives.

In the field of mathematics, the cognitive processes involved in the Revised Bloom’s Taxonomy incorporate characteristics specific to the area of knowledge as direct complements. For instance, symbols, concepts, formulas, propositions, or operational procedures are recalled; reasoning processes, theorems, or explicit data from exercises are understood; mechanical procedures or methods for solving similar tasks are applied; abstract expressions, the rationale behind hypotheses, or relationships between different notions are analyzed; various approaches to reaching a solution or techniques for tackling the same problem are evaluated; and interpretative graphs, innovative proposals, or extrapolations to other mathematical contexts and scientific-social disciplines are created. According to Radmehr and Drake (2018), this taxonomy holds the greatest potential for the entire educational process in mathematics.

On the other hand, the so-called PASS theory of intelligence, formulated by Das et al. (1994), postulates the existence of four cognitive processes involved in mental activity, which typically operate in an interrelated manner: planning, attention, simultaneous processing, and successive processing. Planning involves designing or developing a work plan; attending refers to selecting and maintaining focus on a specific stimulus; simultaneous processing entails integrating separate stimuli into a whole; and successive processing consists of establishing the sequential order of a series of stimuli.

These PASS processes are closely linked to the actions required for solving mathematical tasks. Thus, planning, which is the predominant cognitive process in mathematics, enables the development of methods for solving problems when solutions are not immediately apparent (Tellado, 2001); attention facilitates intense and sustained concentration to perform a specific mathematical task (Iglesias-Sarmiento et al., 2017); simultaneous processing is correlated with number identification, automatic execution of operations, and problem comprehension (Deaño et al., 2006), and successive processing is associated with calculation sequence, mental arithmetic, and the step-by-step resolution of problems (Iglesias-Sarmiento et al., 2014).

Different studies have examined the enhancement of PASS processes in mathematical learning. Chronologically, Kirby and Williams (1991) identify difficulties related to planning, such as reliance on random and inadequate solutions, the use of incorrect strategies, and failure to implement the "trial-and-error" method effectively. Tellado (2001) proposes an intervention model for the class-group that improves planning functions in arithmetic operations through self-reflective verbalization. Iglesias-Sarmiento et al. (2014) highlight a significant relationship between performance in verbal memory, processing speed, PASS processes, and numerical competence, with simultaneous and successive processing emerging as predictors of arithmetic performance. Specifically, in students with learning difficulties, Iglesias-Sarmiento et al. (2017) confirm that simultaneous processing is the only PASS process that predicts arithmetic problem-solving ability. Additionally, attention plays a crucial role in activating higher-order reading comprehension skills (Turégano, 2019), meaning that failure to understand or correctly interpret the statement of a mathematical task may be attributed to deficits in this process. Furthermore, Deaño et al. (2023) demonstrate that the Cognitive Training Program for Mathematics Modules, which focuses on calculation skills and problem-solving based on planning and simultaneous processing, is effective in improving mathematical performance and the PASS processes of the students.

At the same time, the level of complexity of thinking required of students to complete a given task is referred to as cognitive demand or Depth Of Knowledge, abbreviated as DOK. At the end of the 20th century, Webb (1997) develops a cognitive demand model with four levels, ranked from least to most complex: recall thinking, processing thinking, strategic thinking, and extended thinking. In a specifically mathematical context, Smith and Stein (1998) develop a theoretical model to evaluate this framework. Abbreviated as SS, it consists of four categories, ordered from lower to higher complexity: memorization, procedures without connections, procedures with connections, and doing mathematics. This model has only been validated for arithmetic problems, and it does not fully apply to other types of mathematical tasks. Benedicto et al. (2015) modify it to determine the cognitive demand of complex activities based not only on the problem statements, but also on how students solve them. For the cognitive evaluation of geometric tasks, Benedicto (2018) assigns values of 1, 2, 3, and 4 to the SS categories in increasing order of complexity, giving a value of 0 to incorrect solution strategies and unanswered questions. Although originally designed for the cognitive assessment of tasks, Ramos and Casas (2018) apply this model in the field of educational standards and mathematics textbooks in the Algebra block, finding a lack of proper cognitive demand alignment between them. Pincheira and Alsina (2021) also use the SS levels to analyze the cognitive demand of mathematical tasks designed by prospective primary education teachers. Although these authors identify a variety of mathematical tasks, they find that those tasks with a low level of cognitive demand predominantly prevail.

For its part, the National Council of Teachers of Mathematics (2014) has accredited the DOK model to assess both the activities proposed to students, allowing for the design of tasks suited to different purposes, including differentiated instruction, and addressing students with different abilities. Olivares et al. (2020) emphasize the importance of ensuring that the mathematical tasks included in curricula reflect an appropriate DOK level. Furthermore, Parrish and Bryd (2022) argue that the consistent implementation of "cognitively demanding" tasks enhances students´ conceptual understanding of mathematics.

The Webb, SS models, and the RBT and PASS cognitive processes exhibit certain interconnections. In the field of mathematics, considering the actions specified in each of them, we establish the correspondences presented in Figure I.

FIGURE I. Correspondences between the RBT, Webb, SS, and PASS models

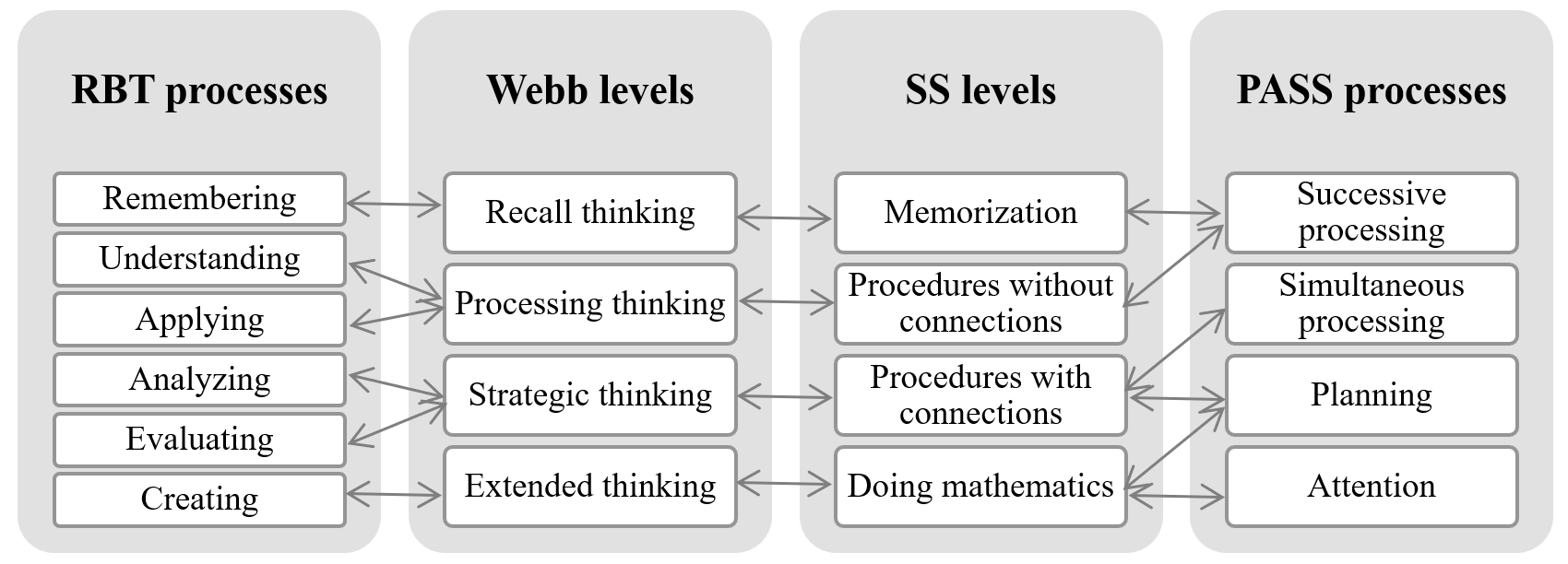
Source: Compiled by the authors

Regarding curricular aspects, Sarmiento and Sarmiento (2023) conducted a study linking the RBT cognitive processes with the descriptors of key competencies in the Primary Education curriculum, to highlight their relationships with knowledge areas and identify potential groupings. Their results show five groups: 1) Artistic Education, related to Linguistic Communication Competence and Cultural Awareness and Expression Competence; 2) Digital Competence; 3) Mathematics and Physical Education, linked to Mathematical, Science, Technology, and Engineering Competence (STEM) and Entrepreneurial Competence; 4) Natural, Social, and Cultural Environment Knowledge, along with Civic and Ethical Values Education, grouped under Citizenship Competence, Personal, Social, and Learning-to-Learn Competence; 6) Spanish Language and Literature and Foreign Language, associated with Multilingual Competence. Thus, their findings confirm that Mathematics contributes to the development of two key competencies: STEM and Entrepreneurial Competence.

Concerning the Secondary Education curriculum (ESO), the study highlights the importance of assessment criteria and mathematical domains. Assessment criteria play a essential role in the educational process, as they establish a set of fundamental knowledge, that integrates skills, competencies, and attitudes in each facet of the subject, ensuring that learning is considered satisfactory. Cognitively, Organic Law 3/2020, which amends Organic Law 2/2006 on Education (LOMLOE), stipulates that achievement indicators for assessment criteria should incorporate cognitive processes in various application contexts and be connected to all mathematical domains. Subsequently, Royal Decree 217/2022 establishes the framework and minimum educational requirements for this stage, defining its objectives, key and specific competencies, assessment criteria, fundamental knowledge, and learning scenarios. Specifically, the structure and curriculum of ESO in the Autonomous Community of Galicia are outlined in Decree 156/2022, which defines assessment criteria as "benchmarks indicating the expected levels of student performance in situations or activities related to the objectives of each subject or area at a given stage of their learning process". Each assessment criterion is linked to a subject objective. However, López (2022) disapproves of them for being merely indicative and, consequently, are difficult to interpret when unequivocally determining students´ academic achievement.

In the field of mathematics, real-life problems are solved concerning quantity, the shape and size of objects, and the randomness of events. Each of these variables requires specific knowledge and skills, collectively known as mathematical domains. The content of Mathematics subjects is structured around six domains: numerical, metric, geometric, algebraic, stochastic, and socio-affective. Each of these encompasses a distinct set of actions aimed at fostering students´ mathematical competence. These domains enable content to expand its link to academic years through transversal connections, allow for the functional application of knowledge, and provide the flexibility needed to establish interconnections between them (Royal Decree 217/2022). It is important to emphasize that the socio-affective domain should not be considered the least mathematical. On the one hand, it includes enthusiasm for rational thinking and strategies that strengthen self-esteem when challenged by incorrect problem-solving approaches, difficulties in grasping certain concepts, operational errors... On the other hand, in its role in promoting gender equality, it offers an approach to mathematics designed to prevent female students from perceiving themselves as less capable than their male counterparts. Additionally, it ensures that collaborative learning is structured so that all students actively participate in each assigned task, fostering peer support and preventing disengagement. Furthermore, mathematical domains are not isolated categories, so certain knowledge belongs to more than one; this is the case for operational knowledge, which is addressed both from a numerical and from an algebraic domain.

Ruiz-Hidalgo et al. (2019) highlight the inherent global nature of mathematical domains, as it places equal emphasis on conceptual understanding and the development of computational skills and techniques. Furthermore, the interaction between mathematical content and domains has been analyzed by the Spanish Mathematics Committee (2021), which presented a study identifying the content areas that should receive more or less focus at different educational stages to effectively develop mathematical domains.

With the aforementioned references, the present research aims, as a general objective, to identify the cognitive processes associated with the Revised Bloom’s Taxonomy and the PASS model, within the assessment criteria of Mathematics in the ESO curriculum in the Autonomous Community of Galicia. All of this with the purpose of identify potential “cognitive mismatches” in this educational stage and propose relevant recommendations for improving their implementation in the classroom. Accordingly, the specific objectives are:

• To determine the predominant cognitive demand within the assessment criteria for each mathematical domain.
• To quantify the cognitive demands present in the assessment criteria in relation to the academic year.

Method

The present study is part of a broader research project (Tugores, 2024) aimed at determining the relationship between cognitive processes and the mathematics curriculum in ESO, knowing and analyzing both its curriculum and the most commonly used didactic materials by teachers for the instruction of the subject. The present study focuses exclusively on the curricular perspective.

A multimethod research approach is adopted, following a concurrent nested design with a dominant model (Hernández-Sampieri, 2006). The method guiding the study, used to identify cognitive demand, is qualitative and is enriched with quantitative data and a descriptive approach, allowing for the quantification of the demands present in the assessment criteria and facilitate the characterization and manifestation of a given phenomenon by assessing various components or dimensions (Hernández-Sampieri, 2006).

In Spain, each autonomous community establishes its own ESO academic curricula; for this study, the curriculum of Galicia is selected. A content analysis of Decree 156/2022 is conducted, where the units of analysis correspond to the assessment criteria in mathematics. These criteria are categorized according to mathematical domains and academic years. As noted by Colás and De Pablos (2012), content analysis is the most appropriate methodological approach for the study of legislation. Thus, a total of 186 assessment criteria are analyzed, whose distribution by academic years and domains is shown in Table I.

TABLE I. Assessment criteria by academic years and mathematical domains

Source: Compiled by the authors

Instrument

For data collection, an ad hoc rubric is used for each mathematical domain, adopting a double-entry table format, in which the RBT and PASS cognitive processes associated with each of the assessment criteria in Decree 156/2022 are indicated (see Tables III and IV). Given that the contents of each academic year are sequentially linked to those of preceding years, the assessment criteria exhibit the same continuity. The rubric was reviewed and validated by three experts, two from the area of Didactics of Mathematics and one with extensive psychometric knowledge, all of them familiar with the variable being quantified. (Hernández-Sampieri, 2006).

The application of the RBT and PASS scales to the units of analysis yielded Cronbach’s alpha coefficients of .748 and .726, respectively, confirming their reliability. The rubric was independently applied to the assessment criteria by two of the authors, achieving a high level of inter-rater agreement (Cohen’s kappa coefficient = .821), and, in cases of discrepancy, the assessment of a third evaluator was considered.

The development of this instrument is based on multiple sources: Decree 156/2022, the cognitive processes defined in RBT, the processes of the PASS model, and the corresponding cognitive actions outlined in Anderson and Krathwohl (2001). For instance, a definition corresponds to remembering, a classification to understanding, a demonstration to applying, a graph to analyzing and evaluating, and designing a project to creating.

Data Analysis

The data analysis is carried out based on two categories (RBT and PASS) and ten subcategories: six from the RBT category (remembering, understanding, applying, analyzing, evaluating, and creating) and four from the PASS category (planning, attention, simultaneous processing, and successive processing). Table II presents these categories, subcategories, and the meaning of the latter.

TABLE II. RBT and PASS categories

Source: Adapted from Anderson & Krathwohl (2001) and Ergin (2021).

Numerical cognitive scales are defined for the RBT and PASS processes. Unlike the scale proposed by Benedicto (2018), these scales are applicable to all types of mathematical problems. The levels of cognitive demand are quantified by assigning a numerical value to each RBT and PASS process within respective ordinal scales, which serve as measurement instruments. The RBT processes are ranked according to their position in the cognitive hierarchy: remembering = 1, understanding = 2, applying = 3, analyzing = 4, evaluating = 5, and creating = 6.

Regarding PASS processes, the assessments of Pérez-Álvarez and Timoneda-Gallart (2000) are considered: “Sequential processing is less complex, less intricate, and more primitive than simultaneous processing, which, in turn, is less intricate than the planning function, the most phylogenetically advanced” (p. 612) and Turégano (2019): “In the PASS model, attention is a more complex process because, in addition to focusing resources on the stimulus to be processed and resisting interference from irrelevant ones, it also involves the minimal necessary mental activation required for a specific task to occur” (p. 10). Accordingly, PASS processes are ranked from least to most complex as follows: successive processing = 1, simultaneous processing = 2, planning = 3, and attention = 4. These scales are termed uniform gradations, based on the hypothesis of "cognitive equidistance" between their respective processes, analogous to the cognitive gradation introduced in a mathematical education, context by Benedicto (2018). The designed matrices are structured with criteria as rows and cognitive processes as columns. A value of 0 is assigned if a process is not involved in a given criterion, while the corresponding scale value is recorded if it is.

A frequency analysis of the cognitive processes is carried out, by mathematical domains and academic years, using the χ² test; the calculation of the mean scores of cognitive demand, along with their confidence intervals, and the comparisons of such scores, using the Kruskal-Wallis H test and the Mann-Whitney U test. Statistical computations are carried out using SPSS software. In all hypothesis tests, decisions are made at a .05 significance level. A difference is considered statistically significant when the p-value is less than .05.

Procedure

All assessment criteria in the mathematics curriculum for all academic years of Compulsory Secondary Education are labelled, identifying the associated level of cognitive demand. In the curriculum for the fourth year, a distinction is made between Mathematics A (applied mathematics) and Mathematics B (academic mathematics), which are denoted as 4th A and 4th B, respectively. Following the guidelines of Decree 156/2022, each label consists of the prefix CE (Assessment Criterion), followed by two digits. The first digit corresponds to a mathematical domain (1 = numerical, 2 = measurement, 3 = spatial, 4 = algebraic, 5 = stochastic, and 6 = socio-affective), while the second digit indicates the criterion’s order within the list. Examples of this labelling system are presented in Tables III and IV. These tables illustrate the process of mapping the cognitive processes from RBT and PASS, respectively, to the assessment criteria in two mathematical domains, for this implementation and analysis, Excel is used.

TABLE III. RBT cognitive processes in an assessment criterion for 1st and 2nd year of ESO

Source: Compiled by the authors.

TABLA IV. PASS cognitive processes in an assessment criterion for 1st, 2nd and 3rd year of ESO

Source: Compiled by the authors.

Results

In the Mathematics subjects of ESO, a total of 186 assessment criteria have been analyzed, but considering their propaedeutic nature, only 57 are distinct (30.6%). Within these criteria, a total of 678 cognitive processes have been identified. Next, the frequencies and the existence of significant differences in cognitive demand presented by the evaluation criteria are examined, according to the RBT and PASS processes.

RBT Cognitive Processes in the Assessment Criteria

Overall, the applying process stands out as the most frequent (122, 28.7%), while understanding is the least frequent (33, 7.8%). The frequencies of remembering (63, 14.8%), evaluating (65, 15.3%), and analyzing (66, 15.5%) are relatively similar, whereas the frequency of creating is slightly higher (76, 17.9%). The χ² test supports statistically significant difference among these proportions (p < .001), but no significant differences are found among the proportions of remembering, analyzing, evaluating, and creating (p = .867).

Table V presents the distribution of RBT cognitive processes across different mathematical domains.

TABLE V. Frequencies of RBT processes by mathematical domains

Source: Compiled by the authors

In each mathematical domain, the predominant process is applying (along with evaluating in the socio-affective domain), while the least frequent is understanding (tied with evaluating in the numerical domain). When considering the total set of criteria, applying remains the most prevalent process; secondly, creating emerges, indicating a high level of cognitive demand. The χ² test does not detect significant difference in the distribution presented in Table V (p = .654). The distribution of the socio-affective domain clearly differs from the others; however, when compared to the aggregated remaining domains, no significant difference is observed (p = .061).

In some cases, the applying process is inherently embedded within the wording of the assessment criterion, as seen in: "solve mathematical problems, by mobilizing the necessary knowledge and applying appropriate tools and strategies" (numerical domain, first three academic years). On the other hand, the understanding process is often accompanied by others, as illustrated in: "reformulate mathematical problems both verbally and graphically, interpreting data, the relationships between them, and the posed questions while utilizing the necessary technological tools" (algebraic domain, 4th A), where applying and creating also play a role.

Actions such as debating, expressing opinions, or making judgments are actions closely linked to the formulation of strategies for solving mathematical tasks, particularly, to the cognitive process of evaluating (Anderson & Krathwohl, 2001). These actions are required in various criteria related to the socio-affective domain, such as: "actively collaborate in teamwork, respecting different opinions, communicating effectively, thinking critically and creatively, and making informed decisions and judgments" (socio-affective domain, 1st, 2nd, and 3rd year).

The distribution of RBT cognitive processes across academic years is presented in Table VI.

TABLE VI. Frequencies of RBT processes in assessment criteria by academic year

Source: Compiled by the authors

In all academic years, applying and understanding occupy the first and last positions, respectively. The assessment criteria for the first, second, and third years of ESO are nearly identical, as are those for 4th A and 4th B. Across the first three years, 21 out of 23 criteria (91.3%) are repeated, while in the fourth year, 23 out of 34 distinct criteria (67.6%) coincide. This situation explains why Table VI reflects nearly identical quantities for each cognitive process across the first three years on one hand, and the two fourth-year courses on the other, with frequency differences not exceeding two points. For this reason, Table VII is prepared, grouping the academic years into two distributions.

TABLE VII. Frequencies of RBT processes by grouped academic years

Source: Compiled by the authors

In the first three years, the predominant process is applying, which corresponds to an intermediate level of cognitive demand, followed by remembering, the lowest-hierarchy RBT process. In the two fourth-year courses, applying remains the most frequent process, but it is followed by creating (the highest-hierarchy cognitive process). The χ² test does not indicate significant difference in the distribution shown in Table VII (p = .231).

The RBT cognitive demand, considering the mean score based on the uniform gradation of all processes within the assessment criteria, is 3.62 (σ = 1.63), exceeding the scale mean (3.5) and falling between the values of applying (3) and analyzing (4). This mean corresponds to 5.25 on a 0-to-10 scale, with a 95% confidence interval of (4.94, 5.56). The mean scores by mathematical domain can be observed in Graph I.

GRAPH I. Mean level of RBT cognitive demand for each mathematical domain

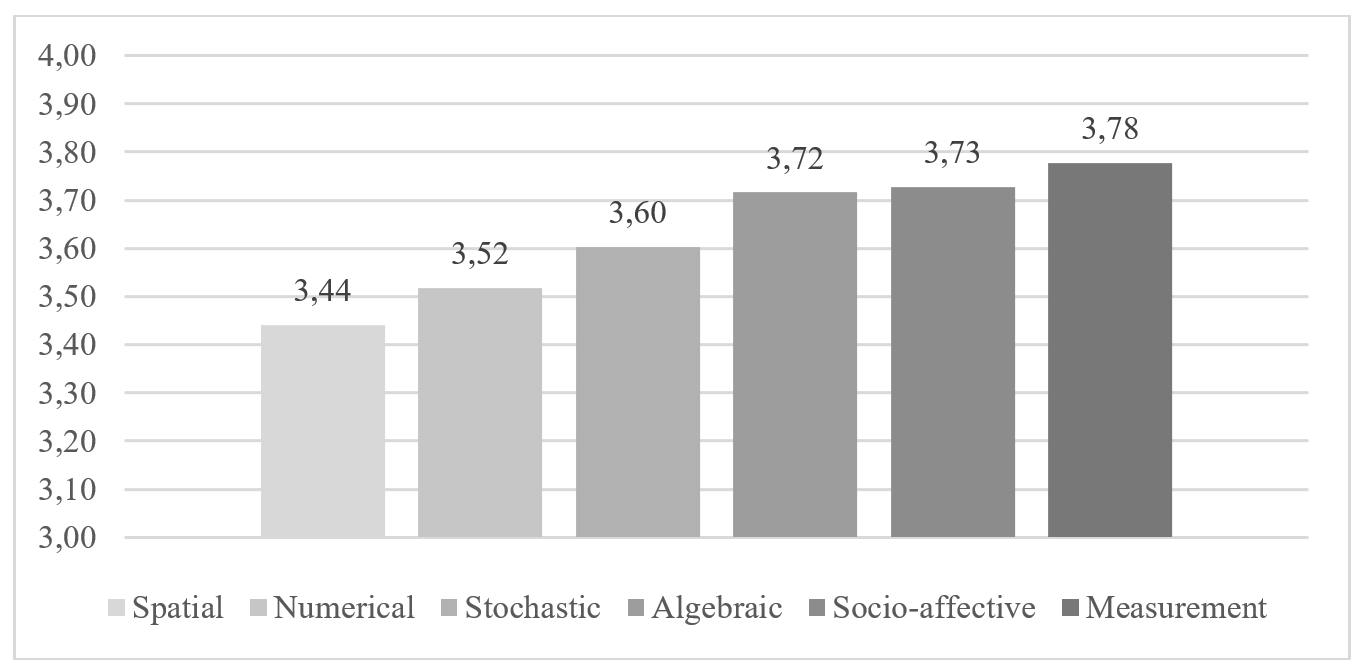
Source: Compiled by the authors

The measurement domain (3.78) exhibits the highest RBT cognitive demand, primarily due to the minimal involvement of remembering and understanding processes in its assessment criteria. The mean scores obtained by the socio-affective domain (3.73) and algebraic domain (3.72) are very close. The Kruskal-Wallis H test supports the equality of these means (p = .838).

For the combined first three years of ESO, the mean score on a 0-to-10 scale is 4.92, while for the two fourth-year courses, it is 5.66. The Mann-Whitney U test rejects the equality of these means (p = .025), indicating that cognitive demand is higher in the final year (4th A and 4th B).

PASS Cognitive Processes in the Assessment Criteria

Simultaneous processing is the most frequently occurring cognitive process (80, 31.6%), while successive processing is the least frequent (52, 20.6%). Planning and attention exhibit similar frequencies (61, 24.1%, and 60, 23.7%, respectively). The χ² test does not indicate significant difference among these proportions (p = .383). Table VIII presents the frequencies of PASS cognitive processes for each mathematical domain.

TABLE VIII. Frequencies of PASS processes by mathematical domains

Source: Compiled by the authors

Simultaneous processing is the predominant process for all domains, except for algebraic and stochastic ones, in which planning stands out. In the stochastic domain, planning appears alongside successive processing in equal measure. The χ² test does not support significant difference in the distribution presented in Table VIII (p = .106), a conclusion that would be reached with greater certainty if the algebraic and stochastic domains were excluded (p = .605).

An example of simultaneous processing can be observed in the criterion: "relate mathematical knowledge and experiences to form a coherent whole" (4th A). Meanwhile, the criterion: "communicate information, using appropriate mathematical language to describe, explain, and justify reasoning, procedures, and conclusions", which belongs to the first three years of Secondary Education, illustrates the emphasis placed on planning within the stochastic domain.

Table IX displays the distribution of PASS process frequencies by course levels, grouping the first three years together and, separately, the two fourth-year courses corresponding to Applied Mathematics and Academic Mathematics.

TABLE IX. Frequencies of PASS processes by grouped academic years

Source: Compiled by the authors

Simultaneous processing stands out as the most frequent process in the first three years. In the fourth year, all cognitive processes exhibit a similar distribution. The χ² test does not indicate significant difference in the distribution of values shown in Table IX (p = .793).

Regarding PASS cognitive demand, the mean score across all processes is 2.51 (σ = 1.07), closely aligning with the scale mean (2.5). This mean corresponds to 5.03 on a 0-to-10 scale, with a 95% confidence interval of (4.59, 5.56). The mean scores by mathematical domain are graphically represented in Graph II.

GRAPH II. Mean level of PASS cognitive demand for each mathematical domain

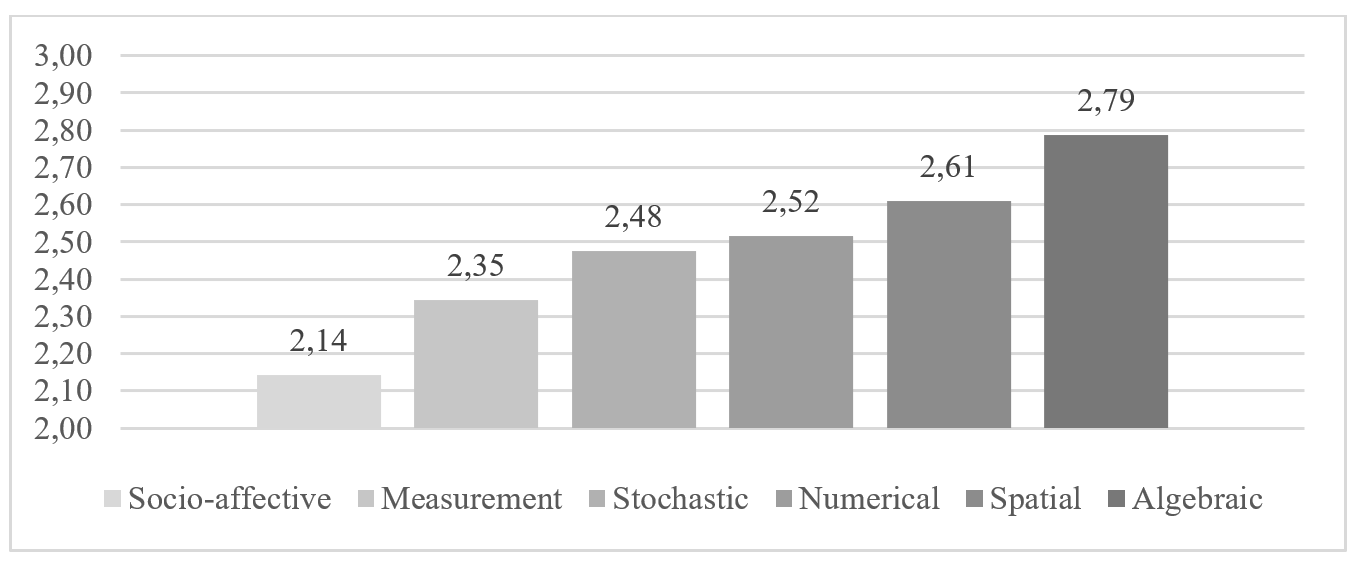
Source: Compiled by the authors

All score values fall within the range of 2.14 to 2.79, with the mean being exceeded in the numerical, spatial, and algebraic domains. The Kruskal-Wallis H test supports the acceptance of score equality among these domains (p = .263). Regarding academic years, the mean score for 1st, 2nd, and 3rd years is 2.47, while for 4th A and 4th B, it is 2.58. The U test allows for accepting their equality (p = .424).

In summary, the obtained results are shown in Table X, which presents the highest and lowest frequencies of RBT and PASS processes, as well as cognitive demand across mathematical domains and academic levels.

TABLE X. Frequencies and cognitive demand of RBT and PASS processes

Source: Compiled by the authors

Discussion and Conclusions

The aim of this study has been to analyze the distribution of the RBT and PASS processes associated with the assessment criteria in Mathematics for Compulsory Secondary Education, as well as to quantify and assess their cognitive demand considering different mathematical domains and academic years. This assessment has been possible through the introduction of a uniform gradation for each cognitive model.

Regarding distribution, the fact that, within the assessment criteria, understanding (33) and applying (122) represent the least and most significantly present RBT processes, respectively, suggests a preference for ensuring that students can effectively utilize the knowledge they acquire, while less emphasis is placed on assessing the extent to which they internalize it. It is likely assumed that using a formula, a rule, a postulate… inherently implies an understanding of the mathematical objects being handled, or that applying theory is a suitable way to consolidate it. This imbalance could be mitigated by placing greater emphasis on aspects that require reflection, ensuring that students assimilate the meaning of mathematical concepts and propositions before applying them in context. Apart from these two extremes, the frequency of the highest hierarchy RBT process, creating (76), stands out with a slight difference, followed by the mid-level complexity process analyzing (66). This is very similar to evaluating (65), which also entails a high cognitive demand, and remembering (63), which represents the lowest cognitive demand. This distribution highlights a form of "cognitive centralization" within the assessment criteria, with a clear predominance of a mid-level cognitive process (applying) and an equitable distribution of the remaining processes, except for understanding, which is notably underrepresented.

This distribution is also consistent across the different mathematical domains, where applying is always the most frequently identified cognitive process in the corresponding assessment criteria. However, differences are observed in second place: creating in the algebraic, stochastic, and measurement domains, associated with a high level of cognitive demand; analyzing is dominant in the numerical domain, representing a medium level of complexity; while remembering is the most recurrent in the spatial domain, associated with the lowest cognitive demand.

Considering the different academic years in ESO, by the fourth academic year, while applying remains the most frequent cognitive process, the two lower-order RBT processes (remembering and understanding) lose prominence in favour of the two higher-order ones (creating and evaluating), whose sum of frequencies more than doubles that of the first two. This shift suggests that remembering and understanding should already be mastered by the time students reach the final year of the stage.

Undoubtedly, a higher-order process may require less effort than a lower-order one; for instance, finding an immediate example is easier than recalling a long definition. Therefore, if this category were assessed numerically, an additional numerical value could be incorporated to the uniform gradations, establishing new and more comprehensive hierarchical cognitive scales. This aligns with the modification made by Benedicto et al. (2015) to the Smith and Stein (1998) model by introducing a category they call “required effort”.

On the other hand, given that applying is the most frequent RBT process, one would expect successive processing to be the predominant PASS process, as there is an established association between applying and successive processing (Figure I). This is based on the fact that applying involves carrying out different mathematical sequences, such as, for example, the very common chain: recognizing a formula, linking operations to arrive at a solution, and verifying its correctness. However, the prevailing process, both in the analysis by mathematical domains and by academic years, is simultaneous processing.

The cognitive demands of RBT and PASS, as explicitly stated in the assessment criteria, can be considered to meet a “cognitive passing grade”. These demands are balanced across mathematical domains. However, a higher RBT demand, but not PASS, is observed in the two Mathematics subjects of the 4th year of ESO compared to those of the first three academic years. This “cognitive leap” could be mitigated by increasing the level of rigor at the end of the 3rd year. Therefore, the role of the teacher is crucial, as they are responsible for the implementation of the curriculum in the classroom. As Ramos and Casas (2018) state, “if a true alignment between educational standards, textbooks, and assessments is ensured, it helps improve curriculum implementation processes, better evaluate assessment results, and engage teachers in improvement processes” (p. 1134).

Although mathematics teachers, according to Parrish and Byrd (2022), strive to maintain the cognitive demand of the tasks implemented, this does not necessarily contribute to increasing mathematical competence. Having a quantification of curricular demand now makes it possible to establish a threshold that the level of rigor should not exceed, if the goal is to increase the complexity of classroom tasks, as suggested by these authors. In the case of pre-service teachers, Pincheira and Alsina (2021) confirm a trend of this group (81.8%) to design low-level tasks for their students. If the cognitive demand levels of the RBT and PASS processes in the examined assessment criteria are considered separately, the resulting distributions are 51.3% and 47.8%, respectively. This suggests that future teachers set the “cognitive bar” relatively low compared to students´ theoretical capabilities and contrary to the expectations set by the assessment criteria.

Ramos and Casas (2018) argue that if the proportional distribution of Smith and Stein’s (1998) levels is similar across educational standards, textbooks, and assessments, then curriculum implementation improves, assessment results gain more significance, and teachers become more involved. Nevertheless, these authors do not provide a numerical representation of cognitive demand. The fact that this study does so, in a broader context than learning standards, enables comparisons between different demands, independent of how cognitive processes are distributed.

The results obtained have implications for teaching practice, as this study can serve as a reference for teachers when selecting tasks that align with assessment criteria, based on their respective mathematical domains and the academic year of ESO in which they are implemented. This selection should consider students’ specific characteristics, prior classroom activities, and the reinforcement or attenuation of particular content, among other factors. Teachers can periodically adjust the cognitive demand of activities to ensure that their complexity and the distribution of cognitive processes remain aligned with curricular requirements. Additionally, classroom diversity can be addressed by balancing the cognitive load of tasks with students’ abilities, especially in lower ESO levels. Furthermore, understanding the distribution of cognitive processes by mathematical domains and their associated cognitive demands may be valuable when designing didactic scenarios that integrate multiple mathematical domains, if the aim is for such interactions between mathematics and real-world contexts to align with what the curriculum establishes.

Limitations

A key limitation of this study lies in the inherent subjectivity involved in determining the cognitive processes associated with certain assessment criteria, whose wording is overly generic. To mitigate this issue, a dual coding process has been implemented in such cases.

Another difficulty has been the inability to compare the values obtained in this research with “individualized” cognitive demands, those that result from the specific way each teacher designs certain tasks to practically develop the assessment criteria.

Prospective

One of the advantages of this analysis is that it provides an instrument and procedure that can be extrapolated to Mathematics curricula at other educational stages or even to different subjects, enabling appropriate comparisons by academic years or mathematical domains within the framework established by Decree 156/2022. Furthermore, cognitive demand levels could be assessed in Secondary Education Mathematics curricula from other autonomous communities, allowing for corresponding analogies or differences to be established.

Referencias bibliográficas

Anderson, L. W., & Krathwohl, D. R. (2001). A taxonomy for learning, teaching, and assessing: A revision of Bloom’s taxonomy of educational objectives. Longman.

Benedicto, C. (2018). Diseño y aplicación de un instrumento para valorar la demanda cognitiva de problemas matemáticos resueltos por estudiantes de enseñanza obligatoria: el caso de las altas capacidades [Tesis de doctorado, Universidad de Valencia]. RODERIC. https://roderic.uv.es/handle/10550/66468

Benedicto, C., Jaime, A., & Gutiérrez, A. (2015). Análisis de la demanda cognitiva de problemas de patrones geométricos. En C. Fernández, M. Molina, & N. Planas (Eds.), Investigación en Educación Matemática XIX (pp. 153-162). SEIEM. https://rua.ua.es/dspace/handle/10045/51384

Colás, P., & De Pablos, J. (2012). Aplicaciones de las tecnologías de la información y la comunicación en la investigación cualitativa. Revista Española de Pedagogía, 251, 77-92. https://dialnet.unirioja.es/servlet/articulo?codigo=3803557

Comité Español de Matemáticas. (2021). Bases para la elaboración de un currículo de Matemáticas en Educación no Universitaria. https://bit.ly/3ytlGg1

Das, J. P., Naglieri, J. A., & Kirby, J. R. (1994). Assessment of cognitive processes: The PASS theory of intelligence. Allyn and Bacon.

Deaño, M., Alfonso, S., Diniz, A. M., Iglesias-Sarmiento, V., & Das, J. P. (2023). Math modules training improves math achievement & associated cognitive processing. Psychology, 14, 1053-1069. https://doi.org/10.4236/psych.2023.146057

Deaño, M., Alfonso, S., & Fernández, M. J. (2006). El D.N: CAS como sistema de evaluación cognitiva para el aprendizaje. En Formación del profesorado para atender a las necesidades específicas de apoyo educativo: Actas de la XXXII Reunión Científica Anual.

Decreto 156/2022, de 15 de septiembre, por el que se establecen la ordenación y el currículo de la Educación Secundaria Obligatoria en la Comunidad Autónoma de Galicia. Diario Oficial de Galicia, 183, 26 de septiembre de 2022, 50010-50542. https://bit.ly/3RU7vIU

Ergin, Ü. T. (2021). Testing the effectiveness of PASS theory-based cognitive games on students’ cognitive processing areas and academic performance. HAYEF: Journal of Education, 18(3), 517-538. https://doi.org/10.5152/hayef.2021.21027

Hernández-Sampieri, R. (2006). Definición del alcance de la investigación a realizar: exploratoria, descriptiva, correlacional o explicativa. En Metodología de la investigación (pp. 57-68), McGraw-Hill. https://bit.ly/4kiN85q

Iglesias-Sarmiento, V., Alfonso, S., Conde, A., & Deaño, M. (2014). Predictores del rendimiento aritmético en 4º de Educación Primaria. International Journal of Developmental and Educational Psychology, 3(1), 223-232. https://revista.infad.eu/index.php/IJODAEP/article/view/497

Iglesias-Sarmiento, V., Deaño, M., Conde, A., Alfonso, S., Limia, S., & Tellado, F. (2017). Resolución de problemas aritméticos en alumnos con dificultades de aprendizaje y TDAH. International Journal of Developmental and Educational Psychology, 3, 167-176. https://revista.infad.eu/index.php/IJODAEP/article/view/909

Kirby, J. R., & Williams, N. (1991). Learning problems: A cognitive approach. Kagan and Woo.

Ley Orgánica 3/2020, de 29 de diciembre, por la que se modifica la Ley Orgánica 2/2006, de 3 de mayo, de Educación. BOE núm. 340, de 30 de diciembre de 2020. https://www.boe.es/boe/dias/2020/12/30/pdfs/BOE-A-2020-17264.pdf

López, F. (2022). El enfoque del currículo por competencias: un análisis de la LOMLOE. Revista Española de Pedagogía, 281, 55-68. https://bit.ly/4bL60Ff

National Council of Teachers of Mathematics. (2014). Principles to actions: Ensuring mathematical success for all. NCTM. https://bit.ly/4hGwI57

Olivares, D., Lupiáñez, J. L., & Segovia, I. (2020). Roles and characteristics of problems solving in the mathematics curriculum: A review. International Journal of Mathematical Education in Science and Technology, 52(7), 1079-1096. https://dx.doi.org/10.1080/0020739X.2020.1738579

Parrish, C. W., & Bryd, K. O. (2022). Cognitively demanding tasks: Supporting students and teachers during engagement and implementation. International Electronic Journal of Mathematics Education, 17(1), em0671. https://doi.org/10.29333/iejme/11475

Pérez-Álvarez, F., & Timoneda-Gallart, C. (2000). La dislexia como disfunción del procesamiento secuencial. Revista de Neurología, 30(7), 614-619. https://bit.ly/4hPNbn7

Pincheira, N., & Alsina, Á. (2021). Explorando la demanda cognitiva de tareas matemáticas de búsqueda de patrones diseñadas por futuros profesores de Educación Primaria. En P. D. Diago, D. F. Yáñez, M. T. González-Astudillo, & D. Carrillo (Eds.), Investigación en Educación Matemática XXIV (pp. 489-496). SEIEM. https://www.seiem.es/docs/actas/24/Comunicaciones/489.pdf

Radmehr, F., & Drake, M. (2018). Revised Bloom’s taxonomy and major theories and frameworks that influence the teaching, learning, and assessment of mathematics: A comparison. International Journal of Mathematical Education in Science and Technology, 50(6), 895-920. https://doi.org/10.1080/0020739X.2018.1549336

Ramos, L. A., & Casas, L. M. (2018). Demanda cognitiva de estándares educativos y libros de texto para la enseñanza del álgebra en Honduras. Bolema, 32(62), 1134-1151. http://dx.doi.org/10.1590/1980-4415v32n62a19

Real Decreto 217/2022, de 29 de marzo, por el que se establece la ordenación de las enseñanzas mínimas de la Educación Secundaria Obligatoria. Boletín Oficial del Estado, 76, de 30 de marzo de 2022, 41571-41789. https://bit.ly/3WHIEMf

Ruiz-Hidalgo, J. F., Flores, P., Ramírez-Uclés, R., & Fernández-Plaza, J. A. (2019). Tareas que desarrollan el sentido matemático en la formación inicial de profesores. Educación Matemática, 31(1), 121-143. https://doi.org/10.24844/EM3101.05

Sarmiento, J. A., & Sarmiento, E. (2023). El currículo de primaria desde la LOMLOE: análisis de las relaciones entre sus elementos. Investigación: Cultura, Ciencia y Tecnología, 29, 61-66. https://dialnet.unirioja.es/servlet/articulo?codigo=9174001

Smith, M. S., & Stein, M. K. (1998). Selecting and creating mathematical tasks: From research to practice. Mathematics Teaching in the Middle School, 3(5), 344-350. https://doi.org/10.5951/MTMS.3.5.0344

Suárez, A. (2016). Introducción a la psicología de los procesos cognoscitivos: compilación y adaptación. Universidad Nacional Abierta y a Distancia (UNAD).

Tellado, F. (2001). Programa cognitivo de intervención en dificultades lógico-matemáticas. [Tesis de doctorado, Universidade de Vigo]. https://dialnet.unirioja.es/servlet/tesis?codigo=137394

Turégano, I. (2019). Relación entre procesos cognitivos PASS y procesos lectores en educación primaria [Trabajo fin de máster, Universidad Internacional de La Rioja]. https://bit.ly/3MGNYK5

Webb, N. L. (1997). Criteria for alignment of expectations and assessments in mathematics and science education (Research Monograph No. 6). National Institute for Science Education, University of Wisconsin-Madison; Council of Chief State School Officers. https://eric.ed.gov/?id=ED414305

Información de contacto / Contact info: Laia Francina Tugores Blanco. Universidade de Vigo, Facultad de Educación y Trabajo Social, Departamento de Matemáticas. E-mail: laia.francina.tugores@uvigo.gal