Demanda cognitiva en criterios de evaluación de Matemáticas del currículo de Galicia: implicaciones docentes

Cognitive demand in Mathematics assessment criteria of the Galician curriculum: teaching implications

https://doi.org/10.4438/1988-592X-RE-2025-409-699

Laia Francina Tugores Blanco

Universidade de Vigo

https://orcid.org/0000-0001-7679-7683

Manuela Raposo-Rivas

Universidade de Vigo

https://orcid.org/0000-0001-7781-7818

Olalla García Fuentes

Universidade de Vigo

https://orcid.org/0000-0001-9084-0078

Resumen

Palabras clave:

procesos cognitivos, criterios de evaluación, currículo, matemáticas, Educación Secundaria

Abstract

Keywords:

Introducción

Los procesos cognitivos son “los procedimientos que lleva a cabo el ser humano para incorporar conocimientos, en los que intervienen facultades muy diversas, como la inteligencia, la atención, la memoria y el lenguaje, que pueden ser conscientes o inconscientes” (Suárez, 2016, p. 5). Con relación a los que intervienen en el aprendizaje, el psicólogo y pedagogo estadounidense Benjamín Bloom publica, a mediados del siglo pasado (1956), una taxonomía que lleva su nombre basada en dos tipos de habilidades de pensamiento, las de orden inferior (LOST), a saber, conocimiento, comprensión y aplicación y las de orden superior (HOST), análisis, síntesis y evaluación. Posteriormente, Anderson y Krathwohl (2001) revisan esta taxonomía estructurando la dimensión cognitiva en seis grandes categorías, que expresan en modo infinitivo para resaltar su carácter dinámico. De menor a mayor nivel de complejidad, son: recordar, comprender, aplicar, analizar, evaluar y crear. De forma abreviada, se identifican por RBT (Revised Bloom’s Taxonomy) y cada una representa objetivos que se desean alcanzar como resultado del aprendizaje. Dichos autores conciben estos procesos de la siguiente forma: recordar consiste en recuperar la información; comprender es explicar ideas o conceptos; aplicar significa usar la información en otra situación familiar; analizar equivale a romper la información en partes para explorar comprensiones y relaciones; evaluar es justificar una decisión o curso de acción; y crear se fundamenta en generar nuevas ideas, productos o maneras de ver las cosas.

En el ámbito de las matemáticas, los procesos implicados en la taxonomía revisada de Bloom añaden características propias del área de conocimiento en forma de complemento directo. Así, se recuerdan símbolos, conceptos, fórmulas, proposiciones o procedimientos operacionales; se comprenden razonamientos, teoremas o datos explícitos de ejercicios; se aplican procedimientos mecánicos o formas de resolver tareas similares; se analizan expresiones abstractas, los porqués de las hipótesis o las relaciones entre distintas nociones; se evalúan diferentes caminos para llegar a un resultado o técnicas para abordar un mismo problema y se crean gráficas interpretativas, propuestas imaginativas o extrapolaciones a otros contextos matemáticos y disciplinas científico-sociales. Según Radmehr y Drake (2018), es la taxonomía con mayor potencial en todo el proceso educacional de las matemáticas.

Por otro lado, la llamada teoría PASS de la inteligencia, formulada por Das et al. (1994), postula la existencia de cuatro procesos cognitivos cuando se realiza una actividad mental, los cuales suelen actuar de manera interrelacionada: planificación, atención, procesamiento simultáneo y procesamiento sucesivo. Planificar es disponer o elaborar un programa de trabajo; atender es seleccionar y mantener un determinado estímulo; procesar simultáneamente es integrar estímulos separados en un todo; y procesar sucesivamente es establecer el orden de una serie de estímulos.

Estos procesos PASS están vinculados con acciones que intervienen en la resolución de actividades matemáticas. Así, la planificación, que es el proceso cognitivo predominante en matemáticas, permite elaborar métodos para resolver un problema cuando su solución no es inmediata (Tellado, 2001); la atención posibilita la concentración intensa y duradera para realizar una determinada tarea matemática (Iglesias-Sarmiento et al., 2017); el procesamiento simultáneo está correlacionado con la identificación de los números, la realización automática de las operaciones y la compresión de los problemas (Deaño et al., 2006) y el procesamiento sucesivo está ligado con la secuencia del cálculo, la aritmética mental y los pasos a dar para la resolución de problemas (Iglesias-Sarmiento et al., 2014).

Diversas investigaciones se han ocupado de la mejora de los procesos PASS en el aprendizaje de las matemáticas. Cronológicamente, Kirby y Williams (1991) determinan dificultades adscritas a la planificación, como intentos de soluciones casuales e inadecuadas, utilización de estrategias incorrectas y el fracaso en el uso del método “ensayo-error”. Tellado (2001) aporta un modelo de intervención para el grupo clase, que mejora el funcionamiento de la planificación en la resolución de operaciones de cálculo a través de la verbalización autorreflexiva. Iglesias-Sarmiento et al. (2014) ponen de manifiesto la relación significativa entre el rendimiento en memoria verbal, la velocidad de procesamiento, los procesos PASS y la competencia numérica, emergiendo el procesamiento simultáneo y el sucesivo como predictores del rendimiento aritmético. En particular, para el alumnado con dificultades de aprendizaje, Iglesias-Sarmiento et al. (2017) verifican que el procesamiento simultáneo es el único proceso PASS predictor de la resolución de problemas aritméticos. Por su parte, la atención adquiere relevancia cuando se han de poner en funcionamiento habilidades de comprensión lectora de orden superior (Turégano, 2019), de manera que no entender el enunciado de una tarea matemática o interpretarlo incorrectamente se puede atribuir a un déficit de este proceso. Por otro lado, Deaño et al. (2023) evidencian que el Programa de Entrenamiento Cognitivo de los Módulos de Matemáticas centrado en las habilidades de cálculo y resolución de problemas que se basan en la planificación y el procesamiento simultáneo, resulta efectivo para mejorar el desempeño matemático y los procesos PASS del alumnado.

Al mismo tiempo, el nivel de complejidad de pensamiento que se exige al alumnado para realizar una determinada tarea se denomina demanda cognitiva o profundidad de conocimiento, abreviadamente DOK por sus siglas en inglés (Depth of Knowledge). A finales del siglo XX, Webb (1997) diseñó un modelo de demanda cognitiva con cuatro niveles, de menor a mayor complejidad: pensamiento memorístico, pensamiento de procesamiento, pensamiento estratégico y pensamiento extendido. En un contexto específicamente matemático, Smith y Stein (1998) elaboran un modelo teórico para evaluar esta propuesta. Abreviado por SS, consta de cuatro categorías, de menor a mayor complejidad: memorización, algoritmos sin conexiones, algoritmos con conexiones y hacer matemáticas. Este modelo solo ha sido validado en problemas de aritmética, habiendo otros tipos a los que no se ajusta. Benedicto et al. (2015) lo modifican para determinar la demanda cognitiva de actividades complejas en base no solo a los enunciados de los problemas, sino también a la forma que tienen los estudiantes para resolverlos. Para evaluar cognitivamente tareas geométricas, Benedicto (2018) asigna los valores 1, 2, 3 y 4 a las categorías SS de menor a mayor complejidad, dando el valor 0 a las estrategias de resolución incorrectas y a las cuestiones no respondidas. Aunque fue creado para la valoración cognoscitiva de tareas, Ramos y Casas (2018) emplean este modelo en el ámbito de los estándares educativos y de los libros de texto de matemáticas en el bloque de Álgebra, constatando que no existe un adecuado alineamiento a nivel de demanda cognitiva entre ellos. También Pincheira y Alsina (2021) utilizan los niveles SS para analizar la demanda cognitiva de tareas matemáticas, en este caso, diseñadas por futuros profesores de Educación Primaria. Aunque los autores identifican una variedad de tareas matemáticas, encuentran que predominan mayoritariamente aquellas que poseen un bajo nivel de demanda cognitiva.

Por su parte, el National Council of Teachers of Mathematics (2014) ha acreditado el modelo DOK para valorar tanto las actividades que se proponen a los estudiantes, lo que permite formular tareas adecuadas para diversas finalidades, como la atención a estudiantes con diferentes capacidades. Olivares et al. (2020) subrayan la importancia de que las tareas matemáticas incluidas en el currículo posean un adecuado nivel DOK. Con todo, Parrish y Bryd (2022) defienden que la constante implementación de las tareas “cognitivamente exigentes” mejora la comprensión conceptual de las matemáticas.

Los modelos Webb, SS y los procesos cognitivos RBT y PASS, guardan ciertas relaciones entre sí. En el ámbito de las matemáticas, teniendo en cuenta las acciones especificadas en cada uno de ellos, establecemos las correspondencias que se indican en la Figura I.

FIGURA I. Correspondencias entre los modelos RBT, Webb, SS y PASS

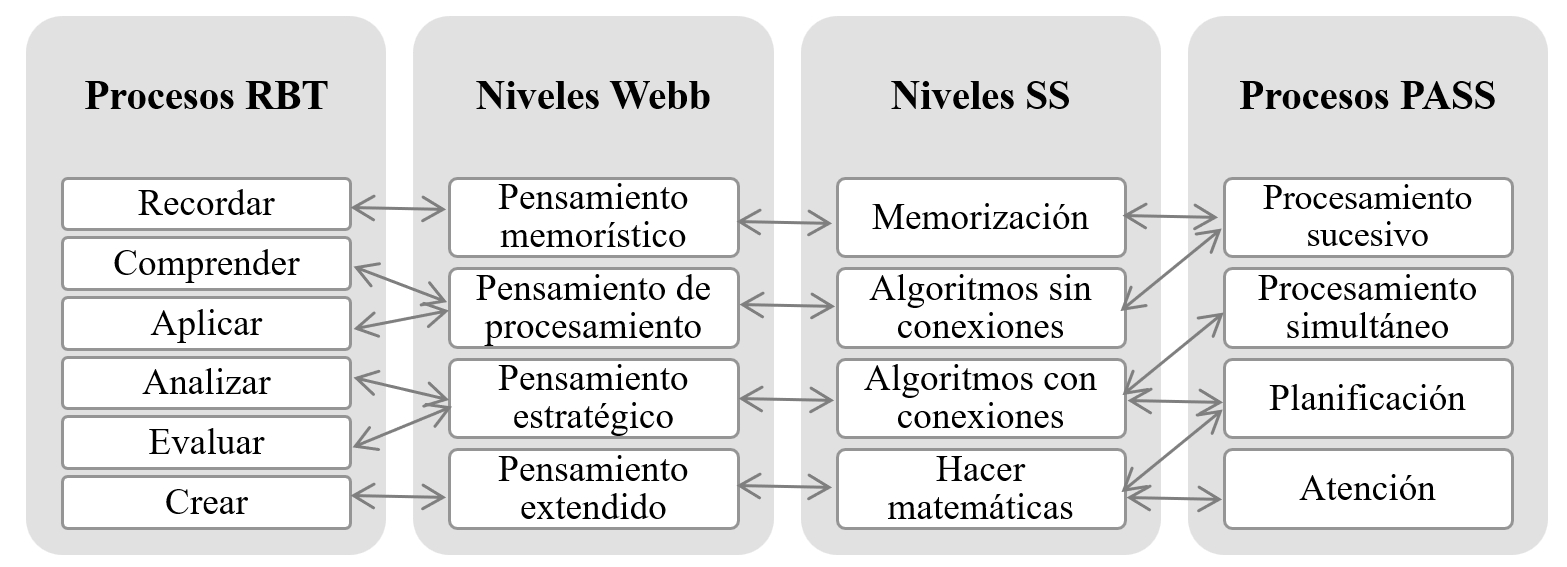
Fuente: Elaboración propia.

En relación con aspectos curriculares, Sarmiento y Sarmiento (2023) realizan un estudio que vincula los procesos cognitivos RBT con los descriptores de las competencias clave del currículo de Educación Primaria, para visibilizar sus relaciones con las áreas de conocimiento e identificar posibles agrupamientos. Sus resultados muestran cinco grupos: 1) Educación Artística relacionada con la Competencia en comunicación lingüística y Competencia en Conciencia y expresión culturales; 2) Competencia digital; 3) Matemáticas y Educación Física vinculadas a la Competencia matemática, ciencia, tecnología e ingeniería y a la Competencia emprendedora; 4) Conocimiento del Medio Natural, Social y Cultural junto con Educación en Valores Cívicos y Éticos agrupadas con la Competencia ciudadana, la Competencia personal, social y de aprender a aprender; 5) Lengua Castellana y Literatura Lengua Extranjera, afines a la Competencia plurilingüe. Constatan, por tanto, la correspondencia del área de Matemáticas en el desarrollo de dos de las competencias clave: la STEM y la emprendedora.

Por lo que respecta al currículo de la Educación Secundaria Obligatoria (ESO), destacan los criterios de evaluación y los sentidos matemáticos. Los criterios de evaluación desempeñan una función esencial en el proceso educativo, en tanto fijan una serie de saberes básicos que integran conocimientos, destrezas y actitudes en cada faceta de la asignatura, para que su aprendizaje sea considerado satisfactorio. En el ámbito cognoscitivo, la Ley Orgánica 3/2020 por la que se modifica la Ley Orgánica 2/2006 de Educación (LOMLOE) establece que los indicadores de logro de los criterios de evaluación contemplen los procesos cognitivos en variados contextos de aplicación y estén conectados a todos los sentidos matemáticos. Posteriormente, el Real Decreto 217/2022 establece la ordenación y las enseñanzas mínimas de la etapa, a la vez que define sus objetivos, competencias clave y específicas, criterios de evaluación, saberes básicos y situaciones de aprendizaje. Particularmente, la ordenación y el currículo de la ESO en la Comunidad Autónoma de Galicia se recogen en el Decreto 156/2022 que define los criterios de evaluación como “referentes que indican los niveles de desempeño esperados en el alumnado en las situaciones o actividades a las que se refieren los objetivos de cada materia o ámbito en un momento determinado de su proceso de aprendizaje”. Cada criterio de evaluación está ligado a un objetivo de la materia. Sin embargo, López (2022) los reprueba por entender que tienen un carácter orientativo y, en consecuencia, son difícilmente interpretables a la hora de determinar inequívocamente el cumplimiento académico de los estudiantes.

En el caso de las matemáticas, se resuelven problemas de la vida real relacionados con la cantidad, con la forma y el tamaño de las cosas y con la aleatoriedad de los sucesos. Cada una de estas variables requiere unos conocimientos y destrezas, que constituyen lo que se conoce como sentido matemático. Los contenidos de las asignaturas de Matemáticas se estructuran en torno a seis sentidos: numérico, métrico, geométrico, algebraico, estocástico y socioafectivo. Cada uno de ellos aglutina un diferenciado conjunto de actuaciones destinadas a que el alumnado desarrolle su competencia matemática. Estos sentidos facilitan que los contenidos amplíen su vinculación a los cursos académicos con una conexión transversal, permiten utilizar los contenidos de una manera funcional y proporcionan la flexibilidad necesaria para establecer conexiones entre ellos (Real Decreto 217/2022). Cabe resaltar que el sentido socioafectivo no se debe entender como el menos matemático de los sentidos ya que, por un lado, incluye el entusiasmo por el pensamiento racional, así como estrategias que fortalecen la autoestima cuando se ve amenazada por planteamientos desacertados de problemas, complicaciones para asimilar algunos conceptos, errores operacionales… Por otro, en su cometido de avanzar en la igualdad de género, proporciona un enfoque de las Matemáticas que pretende evitar que las alumnas puedan sentirse menos cualificadas que los alumnos para su aprendizaje. Asimismo, se ocupa de que el aprendizaje colaborativo se diseñe para que todos los estudiantes participen en cada una de las tareas que se propongan, de forma que unos ayuden a otros y ninguno se descuelgue ni rezague. Además, los sentidos matemáticos no son compartimentos estancos, de forma que hay conocimientos que se ubican en más de uno; tal es el caso de los de tipo operacional, que se abordan desde el numérico y el algebraico.

Ruiz-Hidalgo et al. (2019) destacan la globalidad inherente a los sentidos matemáticos, en cuanto a que prestan la misma atención a la comprensión de conceptos que al aprendizaje de habilidades y técnicas de cálculo. Asimismo, la interacción entre contenidos y sentidos matemáticos ha sido analizada por el Comité Español de Matemáticas (2021), que presentó un estudio enfocado en los contenidos a los que se les debería prestar mayor o menor atención en cada etapa educativa para trabajar los diferentes sentidos matemáticos.

Con los referentes anteriormente descritos, la presente investigación plantea, como objetivo general, identificar los procesos cognitivos asociados a la taxonomía revisada de Bloom y al modelo PASS, en los criterios de evaluación de Matemáticas del currículo de ESO en la Comunidad Autónoma de Galicia. Todo ello con la finalidad de constatar los posibles “desajustes cognitivos” en la etapa y realizar las oportunas consideraciones que permitan mejorar su implementación en el aula. Así, los objetivos específicos son:

• Averiguar la demanda cognitiva predominante en los criterios de evaluación en cada uno de los sentidos matemáticos.
• Cuantificar las respectivas demandas cognitivas presentes en los criterios de evaluación respecto al curso académico.

Método

El estudio que se presenta forma parte de una investigación más amplia (Tugores, 2024) preocupada por determinar la vinculación de los procesos cognitivos con el área de matemáticas en ESO, conociendo y analizando tanto su currículo como el material didáctico más utilizado por los docentes para la enseñanza de dicha asignatura. Se aborda aquí exclusivamente la óptica curricular.

Se realiza una investigación multimétodo, con un diseño anidado concurrente de modelo dominante (Hernández-Sampieri, 2006). El método que guía el estudio, utilizado para identificar la demanda cognitiva, es cualitativo y se enriquece con datos cuantitativos y un enfoque descriptivo, que permiten cuantificar las demandas presentes en los criterios de evaluación y establecer cómo es y cómo se manifiesta un determinado fenómeno evaluando diversos componentes o dimensiones (Hernández-Sampieri, 2006).

Cada comunidad autónoma española establece sus propios currículos académicos de ESO, tomándose en esta investigación el de Galicia. Se lleva a cabo un análisis de contenido del Decreto 156/2022, cuyas unidades de análisis son los criterios de evaluación de Matemáticas, que se clasifican por sentidos matemáticos y cursos académicos. Este tipo de análisis es, según Colás y De Pablos (2012), el más acertado para el estudio de legislación. Así, se analizan un total de 186 criterios, cuya distribución por cursos y sentidos se muestra en la Tabla I.

TABLA I. Criterios de evaluación por cursos y sentidos

Fuente: Elaboración propia.

Instrumento

Para el registro de datos, se utiliza una rúbrica en cada sentido matemático, elaborada ad hoc, que adopta el formato de tabla de doble entrada en la que se señalan los procesos cognitivos RBT y PASS asociados a cada uno de los criterios de evaluación que se indican en el Decreto 156/2022 (ver Tablas III y IV). El hecho de que los contenidos de cada curso estén concatenados con los de los cursos que le anteceden conlleva que suceda lo mismo con los criterios de evaluación. Dicha rúbrica fue revisada y validada por tres expertos, dos del área de Didáctica de las Matemáticas y otro con amplios conocimientos psicométricos, todos ellos familiarizados con la variable que se cuantifica (Hernández-Sampieri, 2006).

La utilización de las escalas RBT y PASS con las unidades de análisis arroja valores de coeficiente alfa de Cronbach de .748 y .726, respectivamente, que avalan su fiabilidad. La aplicación de la rúbrica a los criterios fue realizada separadamente por dos de las autoras, consiguiendo un notable nivel de concordancia (coeficiente kappa de Cohen = .821) y, en caso de discordancia, se tomaba en consideración la valoración de la tercera.

Para la confección de este instrumento se tienen en cuenta: el Decreto 156/2022, los procesos cognitivos RBT, los procesos del modelo PASS y las acciones vinculadas en ellos que se indican en Anderson y Krathwohl (2001). Por ejemplo, una definición se corresponde con recordar; una clasificación, con comprender; una demostración, con aplicar; una gráfica, con analizar y evaluar; un proyecto, con crear.

Análisis de datos

El análisis de datos se realiza atendiendo a dos categorías (RBT y PASS) y diez subcategorías: seis de la categoría RBT (recordar, comprender, aplicar, analizar, evaluar y crear) y cuatro de la PASS (planificación, atención, procesamiento simultáneo y procesamiento sucesivo). La Tabla II recoge dichas categorías, subcategorías y el significado de estas últimas.

TABLA II. Categorías RBT y PASS

Fuente: Elaboración propia a partir de Anderson y Krathwohl (2001) y Ergin (2021).

Además, se definen escalas cognitivas numéricas para los procesos RBT y PASS que, a diferencia de la de Benedicto (2018), son aplicables a todo tipo de problemas matemáticos. Se cuantifican los niveles de demanda cognitiva asignando un guarismo a cada proceso RBT y PASS en sendas escalas ordinales, que constituyen los instrumentos de medición. Los procesos RBT se hacen corresponder con el orden que ocupa cada uno en la jerarquía cognitiva: recordar = 1; comprender = 2; aplicar = 3; analizar = 4; evaluar = 5 y crear = 6.

En cuanto a los procesos PASS, se tienen en cuenta las valoraciones de Pérez-Álvarez y Timoneda-Gallart (2000): “el procesamiento secuencial es menos complejo, menos complicado y más primitivo, que el procesamiento simultáneo, el cual, a su vez, es menos complicado que la función planificadora, la más moderna filogenéticamente” (p. 612) y de Turégano (2019): “en el modelo PASS, la atención es un proceso más complejo porque, además de focalizar recursos hacia el estímulo a procesar y resistirse a la interferencia de otros irrelevantes, supone la activación mental mínima imprescindible para que pueda producirse una determinada tarea” (p. 10). Así, los procesos PASS se ordenan de menor a mayor complejidad de la siguiente forma: procesamiento sucesivo = 1, procesamiento simultáneo = 2, planificación = 3 y atención = 4. Estas escalas reciben el nombre de gradaciones uniformes, porque parten de la hipótesis de que existe “equidistancia cognitiva” entre sus respectivos procesos, tal como sucede en la gradación cognitiva diseñada en un contexto educativo matemático, introducida por Benedicto (2018). Las matrices diseñadas tienen por filas, los criterios y, por columnas, los procesos, con un cero si el proceso no está implicado en el criterio y con su valor en la gradación, si lo está.

Se lleva a cabo un análisis de frecuencias de los procesos cognitivos, por sentidos matemáticos y cursos, utilizándose la prueba χ²; en el cálculo de las puntuaciones medias de la demanda cognitiva, junto con sus intervalos de confianza, y en las comparaciones de tales puntuaciones, mediante las pruebas H de Krustal-Wallis y U de Mann-Whitney. El cálculo de los datos estadísticos se realiza con el software SPSS. En todos los test de hipótesis, las decisiones se toman con un riesgo igual a .05. Se considera que existe diferencia significativa, cuando el nivel de significación p es menor que .05.

Procedimiento

Se etiquetan todos los criterios de evaluación del área de matemáticas en todos los cursos académicos de Educación Secundaria Obligatoria, identificando el nivel de demanda cognitiva que llevan asociados. En el currículo de 4º curso, se distingue entre la asignatura Matemáticas A (aplicadas) y Matemáticas B (académicas), que se denotan, respectivamente, por 4º A y 4º B. Siguiendo el Decreto 156/2022, cada etiqueta está formada por las siglas CE (Criterio de Evaluación), seguidas por dos dígitos, el primero corresponde a un sentido matemático (1 = numérico, 2 = medida, 3 = espacial, 4 = algebraico, 5 = estocástico y 6 = socioafectivo) y el segundo indica el orden que ocupa el criterio en el listado. Se muestran ejemplos de este etiquetado en las Tablas III y IV. Dichas tablas ilustran el proceso de relación entre los procesos cognitivos RBT y PASS, respectivamente, y los criterios de evaluación de dos sentidos matemáticos, para cuya implementación y análisis se utiliza el software Excel.

TABLA III. Procesos cognitivos RBT en un criterio de evaluación de 1º y 2º ESO

Fuente: Elaboración propia.

TABLA IV. Procesos cognitivos PASS en un criterio de evaluación de 1º, 2º y 3º ESO

Fuente: Elaboración propia.

Resultados

En las asignaturas de Matemáticas de ESO se han analizado 186 criterios de evaluación, pero teniendo en cuenta su carácter propedéutico, solamente 57 son diferentes (un 30.6%). En ellos, se han identificado un total de 678 procesos cognitivos. A continuación, se examinan las frecuencias y la existencia de diferencias significativas en la demanda cognitiva que presentan los criterios de evaluación, según los procesos RBT y PASS.

Procesos cognitivos RBT en los criterios de evaluación

De modo general, el proceso aplicar destaca por ser el de mayor frecuencia (122, un 28.7%) y comprender, el de menor (33, un 7.8%). Recordar (63, un 14.8%), evaluar (65, un 15.3%) y analizar (66, un 15.5%) tienen frecuencias similares, en tanto que la frecuencia de crear es algo mayor (76, un 17.9%). La prueba χ² avala la diferencia significativa entre estas proporciones (p < .001), pero no entre las proporciones de recordar, analizar, evaluar y crear (p = .867).

La Tabla V recoge la distribución de los procesos cognitivos RBT en cada uno de los sentidos matemáticos.

TABLA V. Frecuencias de los procesos RBT por sentidos matemáticos

Fuente: Elaboración propia

En cada uno de los sentidos matemáticos, el proceso predominante es aplicar (junto con evaluar en el socioafectivo) y el menos frecuente, comprender (en igualdad con evaluar en el numérico). Si consideramos el total de los criterios, se mantiene aplicar como el más habitual; en segundo lugar, emerge crear, lo que denota un alto nivel de demanda. La prueba χ² no detecta diferencia significativa en el reparto de la Tabla V (p =.654). La distribución del sentido socioafectivo se diferencia claramente del resto, pero si se compara con los otros sentidos agrupados, tampoco se produce diferencia significativa (p = .061).

En algunos casos, el proceso aplicar va implícito en el enunciado del criterio, como en: “resolver problemas matemáticos, movilizando los conocimientos necesarios y aplicando las herramientas y las estrategias apropiadas” (sentido numérico de los tres primeros cursos). Por otro lado, el proceso comprender suele ir acompañado de otros, tal es el caso de: “replantear problemas matemáticos de forma verbal y gráfica, interpretando los datos, las relaciones entre ellos y las preguntas expuestas y utilizando las herramientas tecnológicas necesarias” (sentido algebraico de 4º A), donde también actúan los procesos aplicar y crear.

Debatir, opinar o juzgar son acciones muy ligadas al planteamiento de estrategias para resolver tareas matemáticas, particularmente, al proceso cognitivo evaluar (Anderson y Krathwohl, 2001), y se requieren en diversos criterios relacionados con el sentido socioafectivo, como, por ejemplo: “colaborar activamente en el trabajo en equipo, respetando diferentes opiniones, comunicándose de manera efectiva, pensando de forma crítica y creativa y tomando decisiones y juicios informados" (sentido socioafectivo de 1º, 2º y 3º curso).

La distribución de los procesos cognitivos RBT por cursos se muestra en la Tabla VI.

TABLA VI. Frecuencias de los procesos RBT en los criterios de evaluación por cursos

Fuente: Elaboración propia

En todos los cursos, los procesos aplicar y comprender ocupan el primer y último lugar, respectivamente. Los criterios de evaluación para primero, segundo y tercero de ESO son prácticamente los mismos, como también lo son los de 4º A y 4º B. A lo largo de los tres primeros cursos, se repiten 21 criterios de un total de 23 (91.3%) y en cuarto curso, coinciden 23 de 34 diferentes (67.6%). Esta tesitura motiva que la Tabla VI refleje, para cada proceso cognitivo, cantidades casi idénticas en los tres primeros cursos, por un lado, y en los dos cuartos, por otro, constatando que la diferencia entre las frecuencias no excede de dos puntos. Por esta razón, se elabora la Tabla VII, en la que los cursos se han agrupado en dos reparticiones.

TABLA VII. Frecuencias de los procesos RBT por cursos agrupados

Fuente: Elaboración propia

En los tres primeros cursos, el proceso predominante es aplicar, que se corresponde con un nivel medio de demanda cognitiva, seguido por recordar, que es el de menor jerarquía en los procesos RBT. En los dos cuartos, el de mayor frecuencia también es aplicar, pero seguido por crear (el de mayor jerarquía). La prueba χ² no constata diferencia significativa en el reparto mostrado en la Tabla VII (p = .231).

La demanda cognitiva RBT, considerando la puntuación media con la gradación uniforme de todos los procesos en los criterios de evaluación, es 3.62 (σ = 1.63), por encima de la media de la escala (3.5) y entre los valores de aplicar (3) y analizar (4). Esta media se corresponde con 5.25 en la escala de 0 a 10 y su intervalo de confianza al 95% es (4.94, 5.56). Por sentidos matemáticos, las puntuaciones medias pueden observarse en el Gráfico I.

GRÁFICO I. Nivel medio de demanda cognitiva RBT para cada sentido matemático

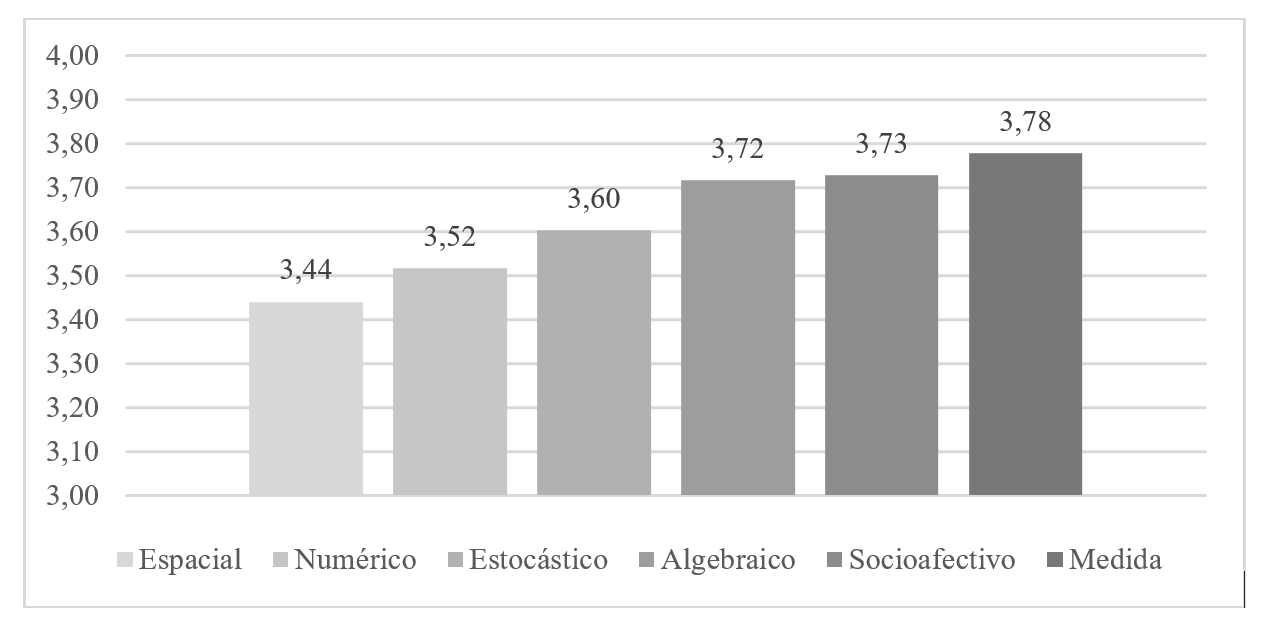
Fuente: Elaboración propia

El sentido de la medida (3.78) es el que presenta mayor demanda cognitiva RBT, fundamentalmente por la escasa implicación de los procesos recordar y comprender en sus criterios de evaluación. Muy próximas están las puntuaciones medias obtenidas por el sentido socioafectivo (3.73) y algebraico (3.72). La prueba H de Krustal-Wallis permite aceptar la igualdad de estas medias (p = .838).

Para el conjunto de los tres primeros cursos de la ESO se obtiene, en la escala de 0 a 10, una media de 4.92 y para los dos cuartos, 5.66. La prueba U de Mann-Whitney rechaza la igualdad de estas medias (p = .025), por lo que es mayor la demanda cognitiva del último curso (4º A y 4º B).

Procesos cognitivos PASS en los criterios de evaluación

El procesamiento simultáneo es el proceso cognitivo de mayor frecuencia (80, 31.6%) y el procesamiento sucesivo, el de menor (52, 20.6%). Los procesos planificación y atención tienen una frecuencia similar (61, un 24.1% y 60, un 23.7%, respectivamente). La prueba χ² descarta diferencia significativa entre estas proporciones (p = .383). La Tabla VIII recoge las frecuencias de los procesos cognitivos PASS para cada sentido matemático.

TABLA VIII. Frecuencias de los procesos PASS por sentidos matemáticos

Fuente: Elaboración propia

El procesamiento simultáneo es el proceso predominante para todos los sentidos, salvo para el algebraico y el estocástico, en los que sobresale la planificación. En el estocástico ex aequo con el procesamiento sucesivo. La prueba χ² no avala diferencia significativa en la repartición mostrada en la Tabla VIII (p = .106), decisión que se tomaría con más holgura si se excluyeran los sentidos algebraico y estocástico (p = .605).

Ejemplo del procesamiento simultáneo se observa en el criterio “relacionar los conocimientos y las experiencias matemáticas entre sí para formar un todo coherente” (4º A). Mientras que el criterio: “comunicar información, utilizando el lenguaje matemático apropiado para describir, explicar y justificar razonamientos, procedimientos y conclusiones”, perteneciente a los tres primeros cursos de Educación Secundaria, ilustra la importancia que se le da a la planificación en el sentido estocástico.

En la Tabla IX se muestra la distribución de las frecuencias de los procesos PASS por cursos, agrupando los tres primeros niveles, por un lado, y por otro, los dos cuartos relativos a Matemáticas aplicadas y a Matemáticas académicas.

TABLA IX. Frecuencias de los procesos PASS por cursos agrupados

Fuente: Elaboración propia

El procesamiento simultáneo destaca sobre el resto de los procesos en los tres primeros cursos. En cuarto, todos los procesos presentan distribución semejante. La prueba χ² no constata diferencia significativa en el reparto de los valores presentes en la Tabla IX (p = .793).

En cuanto a la demanda cognitiva PASS, la puntuación media de todos los procesos es 2.51 (σ = 1.07), próxima al promedio de la escala (2.5). Esta media equivale a 5.03 en la escala de 0 a 10 y su intervalo de confianza al 95% es (4.59, 5.56). Por sentidos matemáticos, las puntuaciones medias se representan gráficamente en el Gráfico II.

GRÁFICO II. Nivel medio de demanda cognitiva PASS para cada sentido matemático

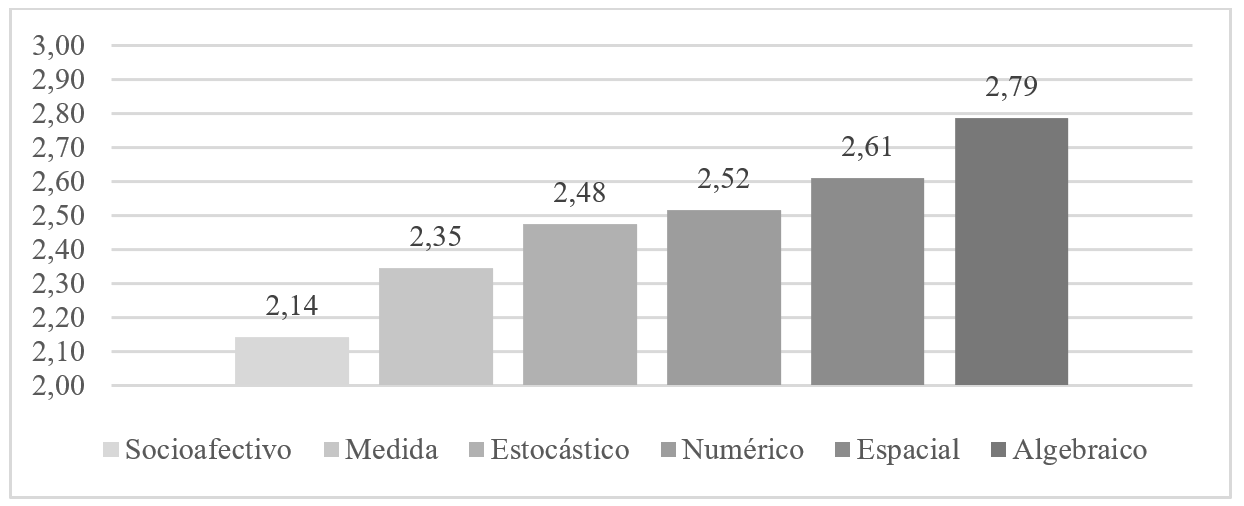
Fuente: Elaboración propia

Los valores de todas las puntuaciones están comprendidos entre 2.14 y 2.79, superándose la media en los sentidos numérico, espacial y algebraico. La prueba H permite aceptar su igualdad (p = .263). Teniendo en cuenta los cursos, en 1º, 2º y 3º se obtiene una media de 2.47 y para 4º A y 4º B, 2.58. La prueba U permite aceptar su igualdad (p = .424).

A modo de síntesis, los resultados obtenidos se muestran en la Tabla X, considerando la mayor y menor frecuencia de los procesos RBT y PASS, así como la demanda cognitiva teniendo en cuenta los diferentes sentidos matemáticos y cursos.

TABLA X. Frecuencias y demanda cognitiva de los procesos RBT y PASS

Fuente: Elaboración propia

Discusión y conclusiones

La finalidad de este estudio ha sido analizar la distribución de los procesos RBT y PASS vinculados a los criterios de evaluación de Matemáticas en Educación Secundaria Obligatoria, así como cuantificar y valorar su demanda cognitiva considerando los diferentes sentidos matemáticos y cursos académicos. Dicha valoración ha sido posible gracias a la introducción de una gradación uniforme para cada modelo cognitivo.

En relación con la distribución, el hecho de que, en los criterios de evaluación, comprender (33) y aplicar (122) son los procesos RBT de menor y mayor presencia significativa, respectivamente, indica que se prima que el alumnado sepa sacar provecho de los conocimientos que adquiere y, en cambio, se concede escasa relevancia a determinar en qué medida los interioriza. Probablemente, se presupone que utilizar una fórmula, una regla, un postulado… lleva implícito haber entendido los objetos matemáticos que se deben manejar o que aplicar la teoría es una buena forma de asentarla. Se podría evitar esta descompensación haciendo más hincapié en aquellas cuestiones que reclaman reflexión, para que el alumnado asimile el significado de los conceptos y proposiciones matemáticas antes de ponerlos en contexto. Al margen de estos dos extremos destacan, con escasa diferencia, la frecuencia del proceso RBT de mayor jerarquía crear (76), seguida por el de complejidad media analizar (66). Muy próximo éste a evaluar (65), asociado también a una alta demanda cognitiva, y a recordar (63), el de menor nivel de demanda. Esto pone de manifiesto una “centralización cognitiva” de los criterios de evaluación, con una clara prevalencia de un proceso cognitivo de nivel medio (aplicar) y una distribución equitativa del resto de procesos, a excepción de la “comprensión” que está escasamente representada.

Esta distribución es también coherente entre los distintos sentidos matemáticos, donde aplicar es siempre el proceso cognitivo más identificado en los correspondientes criterios de evaluación. Sin embargo, se observan diferencias en el segundo lugar: crear en el sentido algebraico, estocástico y de la medida, asociado a un alto nivel de demanda cognitiva; analizar, nivel medio, en el sentido numérico y recordar, menor nivel, en el sentido espacial.

Teniendo en cuenta los cursos académicos de la ESO, al llegar a cuarto, manteniéndose aplicar como el proceso cognitivo más frecuente, los dos procesos RBT de menor jerarquía (recordar y comprender) ceden protagonismo a los dos de jerarquía mayor (crear y evaluar), cuya suma de frecuencias más que duplica la de los dos primeros. Este desplazamiento parece indicar que los procesos recordar y comprender ya deben dominarse al llegar al último curso de la etapa.

Sin duda, un proceso de jerarquía superior puede suponer menos esfuerzo que otro de jerarquía inferior, tal es el caso de encontrar un ejemplo inmediato, que resulta más sencillo que recordar una larga definición. Por ello, si esta categoría se valorase numéricamente, se podría añadir otro guarismo a las graduaciones uniformes y establecer con ambos unas nuevas y más completas escalas jerárquicas cognitivas, en la línea de la modificación realizada por Benedicto et al. (2015) del modelo de Smith y Stein (1998), al introducir una categoría que denominan “esfuerzo requerido”.

Por otro lado, dado que el proceso RBT más frecuente es aplicar, cabría esperar que el proceso PASS predominante fuese el procesamiento sucesivo, ya que existe una asociación entre aplicar y procesamiento sucesivo (Figura I), en base a que aplicar consiste en llevar a cabo diferentes secuencias matemáticas como, por ejemplo, la muy habitual cadena: reconocer una fórmula, encadenar operaciones para llegar a la solución y comprobar que es correcta. Sin embargo, es el procesamiento simultáneo, el imperante tanto en el análisis por sentidos matemáticos como por cursos.

Con respecto a las valoraciones de las demandas cognitivas RBT y PASS que se explicitan en los criterios de evaluación, se pueden calificar con un “aprobado cognitivo”. Dichas demandas están niveladas con respecto a los sentidos matemáticos. Sin embargo, se constata mayor demanda RBT, no así PASS, en las dos asignaturas de 4º ESO que en las de los tres primeros cursos de la etapa, “salto cognitivo” que se podría suavizar intensificando la exigencia del final de 3º ESO. Por ello, el papel del docente es clave, en cuanto responsable del desarrollo del currículo en el aula. Como dicen Ramos y Casas (2018), “si se asegura un verdadero alineamiento entre los estándares educativos, los libros de texto y las evaluaciones, se ayuda a mejorar los procesos de implementación del currículo, a valorar con mejor criterio los resultados de las evaluaciones y a involucrar a los docentes en los procesos de mejora” (p. 1134).

Aunque el profesorado de Matemáticas, según Parrish y Bryd (2022), se esfuerza por mantener la demanda cognitiva de las tareas implementadas, no contribuye a aumentar la competencia matemática. Disponer ahora de una cuantificación de la demanda curricular permite fijar el umbral que el nivel de exigencia no debería sobrepasar, si se opta por incrementar la complejidad de las tareas que se realizan en el aula, como sugieren los citados autores. En el caso de los docentes en formación inicial, Pincheira y Alsina (2021) constatan la tendencia de este profesorado (un 81.8%) a diseñar tareas de bajo nivel para sus estudiantes. Si se hace esta división en el nivel de demanda de los procesos RBT y PASS de los criterios examinados, se obtienen unos equilibrados 51.3% y 47.8%, respectivamente, lo que indica que los futuros docentes colocan el “listón cognitivo” bastante bajo con respecto a las teóricas posibilidades del alumnado y en contra de lo que indican los criterios de evaluación.

Ramos y Casas (2018) afirman que, si las proporciones de los niveles de Smith y Stein (1998) para los estándares educativos, libros de texto y evaluaciones son similares, entonces mejoran los procesos de implementación del currículo, los resultados de las evaluaciones son más valorados y se involucra más a los docentes. Con todo, dichos autores no entran a expresar numéricamente ninguna demanda cognitiva. El hecho de que en este trabajo sí se haga, en un contexto más general que los estándares de aprendizaje, hace posible realizar comparaciones entre demandas, al margen de cómo se distribuyan los procesos cognitivos.

Los resultados obtenidos poseen implicaciones para la práctica docente, ya que el presente estudio puede ser un referente para el profesorado a la hora de escoger las tareas coherentes con los criterios de evaluación, en función del sentido matemático al que pertenezcan y curso de la ESO en el que se ubiquen, teniendo en cuenta las peculiaridades del alumnado, las actividades realizadas con anterioridad en el aula, la intensificación o atenuación de determinados contenidos, etc. Los docentes pueden regular periódicamente la demanda cognitiva de las actividades para que su valor y la distribución de los procesos se alineen con las exigencias curriculares. También es posible atender a la diversidad del aula equilibrando la carga cognitiva de las tareas con las capacidades de los estudiantes, especialmente en los niveles educativos más bajos de la ESO. Así mismo, conocer el reparto de los procesos cognitivos por sentidos y las demandas cognitivas asociadas puede resultar útil al diseñar situaciones didácticas que traten aspectos de diferentes sentidos matemáticos, si se pretende que tales interacciones de las matemáticas con el entorno estén en consonancia con lo que el currículo establece.

Limitaciones

Como limitación del estudio, se puede señalar la inevitable subjetividad a la hora de determinar los procesos cognitivos implicados en algunos criterios, cuya redacción es excesivamente genérica. Para paliar sus efectos, en estos casos, se ha realizado un doble proceso de codificación.

Otra dificultad ha sido la imposibilidad de comparar los valores obtenidos en esta investigación con las demandas cognitivas “individualizadas”, aquellas que son resultado de la particular forma que tiene cada docente de plantear determinadas tareas para desarrollar en la práctica los criterios de evaluación.

Prospectiva

Una de las bondades que posee este análisis es que ofrece un instrumento y procedimiento que es extrapolable a los currículos de Matemáticas de otras etapas educativas o asignaturas, con lo que se podrían realizar las oportunas comparaciones por cursos o sentidos matemáticos en los que rige el Decreto 156/2022. Además, podrían valorarse los niveles de demanda cognitiva en los currículos de Matemáticas de Educación Secundaria de otras comunidades autónomas y establecer las correspondientes analogías o diferencias.

Referencias bibliográficas

Anderson, L. W., & Krathwohl, D. R. (2001). A taxonomy for learning, teaching, and assessing: A revision of Bloom’s taxonomy of educational objectives. Longman.

Benedicto, C. (2018). Diseño y aplicación de un instrumento para valorar la demanda cognitiva de problemas matemáticos resueltos por estudiantes de enseñanza obligatoria: el caso de las altas capacidades [Tesis de doctorado, Universidad de Valencia]. RODERIC. https://roderic.uv.es/handle/10550/66468

Benedicto, C., Jaime, A., & Gutiérrez, A. (2015). Análisis de la demanda cognitiva de problemas de patrones geométricos. En C. Fernández, M. Molina, & N. Planas (Eds.), Investigación en Educación Matemática XIX (pp. 153-162). SEIEM. https://rua.ua.es/dspace/handle/10045/51384

Colás, P., & De Pablos, J. (2012). Aplicaciones de las tecnologías de la información y la comunicación en la investigación cualitativa. Revista Española de Pedagogía, 251, 77-92. https://dialnet.unirioja.es/servlet/articulo?codigo=3803557

Comité Español de Matemáticas. (2021). Bases para la elaboración de un currículo de Matemáticas en Educación no Universitaria. https://bit.ly/3ytlGg1

Das, J. P., Naglieri, J. A., & Kirby, J. R. (1994). Assessment of cognitive processes: The PASS theory of intelligence. Allyn and Bacon.

Deaño, M., Alfonso, S., Diniz, A. M., Iglesias-Sarmiento, V., & Das, J. P. (2023). Math modules training improves math achievement & associated cognitive processing. Psychology, 14, 1053-1069. https://doi.org/10.4236/psych.2023.146057

Deaño, M., Alfonso, S., & Fernández, M. J. (2006). El D.N: CAS como sistema de evaluación cognitiva para el aprendizaje. En Formación del profesorado para atender a las necesidades específicas de apoyo educativo: Actas de la XXXII Reunión Científica Anual.

Decreto 156/2022, de 15 de septiembre, por el que se establecen la ordenación y el currículo de la Educación Secundaria Obligatoria en la Comunidad Autónoma de Galicia. Diario Oficial de Galicia, 183, 26 de septiembre de 2022, 50010-50542. https://bit.ly/3RU7vIU

Ergin, Ü. T. (2021). Testing the effectiveness of PASS theory-based cognitive games on students’ cognitive processing areas and academic performance. HAYEF: Journal of Education, 18(3), 517-538. https://doi.org/10.5152/hayef.2021.21027

Hernández-Sampieri, R. (2006). Definición del alcance de la investigación a realizar: exploratoria, descriptiva, correlacional o explicativa. En Metodología de la investigación (pp. 57-68), McGraw-Hill. https://bit.ly/4kiN85q

Iglesias-Sarmiento, V., Alfonso, S., Conde, A., & Deaño, M. (2014). Predictores del rendimiento aritmético en 4º de Educación Primaria. International Journal of Developmental and Educational Psychology, 3(1), 223-232. https://revista.infad.eu/index.php/IJODAEP/article/view/497

Iglesias-Sarmiento, V., Deaño, M., Conde, A., Alfonso, S., Limia, S., & Tellado, F. (2017). Resolución de problemas aritméticos en alumnos con dificultades de aprendizaje y TDAH. International Journal of Developmental and Educational Psychology, 3, 167-176. https://revista.infad.eu/index.php/IJODAEP/article/view/909

Kirby, J. R., & Williams, N. (1991). Learning problems: A cognitive approach. Kagan and Woo.

Ley Orgánica 3/2020, de 29 de diciembre, por la que se modifica la Ley Orgánica 2/2006, de 3 de mayo, de Educación. BOE núm. 340, de 30 de diciembre de 2020. https://www.boe.es/boe/dias/2020/12/30/pdfs/BOE-A-2020-17264.pdf

López, F. (2022). El enfoque del currículo por competencias: un análisis de la LOMLOE. Revista Española de Pedagogía, 281, 55-68. https://bit.ly/4bL60Ff

National Council of Teachers of Mathematics. (2014). Principles to actions: Ensuring mathematical success for all. NCTM. https://bit.ly/4hGwI57

Olivares, D., Lupiáñez, J. L., & Segovia, I. (2020). Roles and characteristics of problems solving in the mathematics curriculum: A review. International Journal of Mathematical Education in Science and Technology, 52(7), 1079-1096. https://dx.doi.org/10.1080/0020739X.2020.1738579

Parrish, C. W., & Bryd, K. O. (2022). Cognitively demanding tasks: Supporting students and teachers during engagement and implementation. International Electronic Journal of Mathematics Education, 17(1), em0671. https://doi.org/10.29333/iejme/11475

Pérez-Álvarez, F., & Timoneda-Gallart, C. (2000). La dislexia como disfunción del procesamiento secuencial. Revista de Neurología, 30(7), 614-619. https://bit.ly/4hPNbn7

Pincheira, N., & Alsina, Á. (2021). Explorando la demanda cognitiva de tareas matemáticas de búsqueda de patrones diseñadas por futuros profesores de Educación Primaria. En P. D. Diago, D. F. Yáñez, M. T. González-Astudillo, & D. Carrillo (Eds.), Investigación en Educación Matemática XXIV (pp. 489-496). SEIEM. https://www.seiem.es/docs/actas/24/Comunicaciones/489.pdf

Radmehr, F., & Drake, M. (2018). Revised Bloom’s taxonomy and major theories and frameworks that influence the teaching, learning, and assessment of mathematics: A comparison. International Journal of Mathematical Education in Science and Technology, 50(6), 895-920. https://doi.org/10.1080/0020739X.2018.1549336

Ramos, L. A., & Casas, L. M. (2018). Demanda cognitiva de estándares educativos y libros de texto para la enseñanza del álgebra en Honduras. Bolema, 32(62), 1134-1151. http://dx.doi.org/10.1590/1980-4415v32n62a19

Real Decreto 217/2022, de 29 de marzo, por el que se establece la ordenación de las enseñanzas mínimas de la Educación Secundaria Obligatoria. Boletín Oficial del Estado, 76, de 30 de marzo de 2022, 41571-41789. https://bit.ly/3WHIEMf

Ruiz-Hidalgo, J. F., Flores, P., Ramírez-Uclés, R., & Fernández-Plaza, J. A. (2019). Tareas que desarrollan el sentido matemático en la formación inicial de profesores. Educación Matemática, 31(1), 121-143. https://doi.org/10.24844/EM3101.05

Sarmiento, J. A., & Sarmiento, E. (2023). El currículo de primaria desde la LOMLOE: análisis de las relaciones entre sus elementos. Investigación: Cultura, Ciencia y Tecnología, 29, 61-66. https://dialnet.unirioja.es/servlet/articulo?codigo=9174001

Smith, M. S., & Stein, M. K. (1998). Selecting and creating mathematical tasks: From research to practice. Mathematics Teaching in the Middle School, 3(5), 344-350. https://doi.org/10.5951/MTMS.3.5.0344

Suárez, A. (2016). Introducción a la psicología de los procesos cognoscitivos: compilación y adaptación. Universidad Nacional Abierta y a Distancia (UNAD).

Tellado, F. (2001). Programa cognitivo de intervención en dificultades lógico-matemáticas. [Tesis de doctorado, Universidade de Vigo]. https://dialnet.unirioja.es/servlet/tesis?codigo=137394

Turégano, I. (2019). Relación entre procesos cognitivos PASS y procesos lectores en educación primaria [Trabajo fin de máster, Universidad Internacional de La Rioja]. https://bit.ly/3MGNYK5

Webb, N. L. (1997). Criteria for alignment of expectations and assessments in mathematics and science education (Research Monograph No. 6). National Institute for Science Education, University of Wisconsin-Madison; Council of Chief State School Officers. https://eric.ed.gov/?id=ED414305

Información de contacto / Contact info: Laia Francina Tugores Blanco. Universidade de Vigo, Facultad de Educación y Trabajo Social, Departamento de Matemáticas. E-mail: laia.francina.tugores@uvigo.gal