Criticism of the analysis of Construct Validity of the Gifted Rating Scales (GRS 2) Parent Form in Spain; a reply to Tourón et al. (2023)
Crítica del análisis de la validez de constructo de la Escala de Detección de alumnos con Altas Capacidades para Padres (GRS 2); réplica a Tourón et al. (2023)
https://doi.org/10.4438/1988-592X-RE-2024-406-649
José A. Martínez García
https://orcid.org/0000-0003-2131-9101
Universidad Politécnica de Cartagena
Abstract
The objective of this study is to reexamine the methods used to analyze the construct validity of the Gifted Rating Scales (GRS 2) Parent Form in Spain, originally conducted by Tourón et al. (2023). To achieve this, we build upon the proposals of these authors, offering constructive criticism of some of their procedures and suggesting alternative modeling and analysis methods. Our approach is primarily didactic, drawing extensively from the literature on structural equation modeling and psychometrics. Key elements of our critique include the distinction between reflective and formative models, the direction of causality and the underlying equations, the appropriateness of analyzing construct validity within a nomological network beyond factor analysis, and the use of chi-square testing for the structural model. Additionally, we propose various modeling options that align with current research trends in the measurement of high abilities, providing a foundation for future advancements in this discipline.
Keywords: gifted rating scales, high ability, construct validity, confirmatory factor analysis, structural equation modeling, formative models.
Resumen
El objetivo de este trabajo es reexaminar los métodos de análisis de la validez de constructo de la escala de detección de alumnos con altas capacidades para padres (GRS 2) en España, realizados por Tourón et al. (2023). Para ello, partimos de la propuesta de estos autores, criticando de forma constructiva algunos de sus procedimientos, y planteando alternativas de modelización y análisis. De este modo, se emplea un enfoque eminentemente didáctico, basado fundamentalmente en la literatura sobre modelos de ecuaciones estructurales y psicometría. La distinción entre modelos reflectivos y formativos, la dirección de causalidad y las ecuaciones subyacentes, la idoneidad de analizar la validez de constructo en una red nomológica yendo más allá del análisis factorial, y el test del modelo estructural usando la chi-cuadrado, son los principales ejes sobre los que se articula la crítica. Asimismo, se proponen diferentes opciones de modelización que son congruentes con líneas de investigación en medición de altas capacidades, y que podrán servir de base para seguir avanzando en esta disciplina en el futuro.
Palabras clave: escala de detección, altas capacidades, validez de constructo, análisis factorial confirmatorio, ecuaciones estructurales, modelos formativos.
Introduction
Tourón et al. (2023) analyzed the construct validity of the Parent Form of the Gifted Rating Scales (GRS 2) in Spain, utilizing a final sample of 1,109 parents of children and adolescents (ages 4 to 18) with high abilities. The scale, based on an original model with three dimensions—cognitive abilities, creative and artistic abilities, and socio-emotional skills—comprises 20 items distributed among these dimensions. Tourón et al. (2023) adapted the questionnaire to Spanish and conducted a validation study, ultimately identifying four factors: cognitive ability, creative ability, social skills, and emotional control. These factors were grouped into two higher-order factors: cognitive-creative ability and socio-emotional skills, respectively.
However, several methodological procedures and result analyses described by Tourón et al. (2023) are questionable. Both the proposed factorial model, based on a reflective view of measuring high abilities, and the fit indices used to validate the dimensional structure, which are approximate in nature, seriously limit the interpretation of the results.
The objective of this work is to reexamine the analysis methods of the GRS 2 scale. To achieve this, we build upon the proposal of Tourón et al. (2023), offering constructive criticism of some of their procedures and suggesting alternative modeling and analysis methods. Our proposal not only evaluates the suitability of Tourón et al.’s (2023) approach but also encourages reconsideration of some modeling and analysis procedures used in research on high abilities.
We employ a primarily didactic approach, drawing extensively from the literature on structural equation models and psychometrics. The critiques are divided into several key points, which will be developed in the following sections.
Reflective vs. Formative Modeling
We will consider the model presented in Figure I as the basis. In this model, there is a vector of latent variables η whose true scores are unknown, but we can attempt to estimate them through the relationship between these latent variables and a vector of observable indicators y.
FIGURE I. Factorial Model and Extended Model
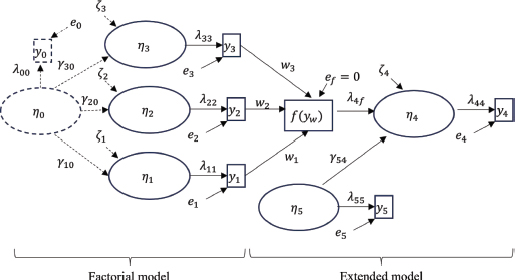
The “factorial” part aims to represent the initial conceptualization of Tourón et al. (2023). It posits a multidimensional model of high abilities: cognitive abilities, creative and artistic abilities, and socio-emotional skills. In Figure I, this model is represented by the latent variables η1, η2, and η3 and the observable indicators (items) y1, y2, y3. As MacCallum and Austin (2000) remind us, latent variables are hypothetical constructs that cannot be directly measured. They are reflected through a series of observable indicators which, as Bollen (2002) explains, are locally independent and define the expected value of the latent variable, which is a non-deterministic function of these indicators.
For the sake of simplification, Figure I shows only one indicator per latent variable, instead of the 6, 7, and 7 indicators, respectively, in the GRS 2 model. This simplification does not affect our initial exposition, although it will be important later. The relationship between the latent variables and their indicators is causal, in line with classical test theory: the variation in the latent variable η1 manifests as a variation in the observable indicator, scaled by the parameter λ11, to which a random error e1 must be added. If the data are parameterized as deviations from the mean of the observable indicators (a common practice in specialized software for this type of analysis that does not affect the covariance structures), the equations relating latent variables and indicators are as simple as (1), representing the first dimension:
This type of causal structure between latent variables and indicators is called reflective (Bollen & Diamantopoulos, 2017), where the indicators are manifestations (effects) of the latent variable. Variations in the latent trait or factor produce variations in the observable indicator, depending on the choice (or estimation, as the case may be) of the scaling factor λ and the error e. The latent variable is scaled with one of its indicators (in this case, the only indicator it has), fixing its value (usually to one, but not necessarily always), indicating that unit variations in the latent variable are reflected in unit variations in the observable indicator (plus random fluctuations).
The “factorial” part of Figure I is completed by the latent variable η0, which can represent various states of the real world. Firstly, it can be seen as a higher-order variable to the multidimensional structure, representing a quality that cannot be measured directly but is causally manifested through dimensions, which can be measured with observable indicators. This type of conceptualization is employed in studies on GRS scales (e.g., Sofologi et al., 2022). Secondly, it can be interpreted as a latent variable that can be measured through an observable indicator y0 and that causally influences the rest of the latent variables. In Figure I, the relationship between latent variables follows a similar expression to (1), which for the first dimension is (2):
where γ10 represents the effect of η0 on η1, and ζ1 is the error made in determining η1.
The usual conceptualization in this area of knowledge is the first one, as shown, for example, in Pfeiffer et al. (2008), where a multidimensional conception of high abilities is proposed with an underlying “g” factor, or general ability factor1. It must be acknowledged that Tourón et al. (2023) are very cautious and do not clearly state this fact, but they seem to imply it surreptitiously when they calculate a “total scale mean,” as we will explain later.
Therefore, since there is a latent factor that cannot be directly measured (we do not have y0), the measurement of dimensions that are manifestations of that factor is proposed. This distinction is crucial because the estimation of the true value2 of η0 must then be done through this specification (3):
Thus, the following equality must be satisfied (4):
Assuming the expected value of the errors e1, e2, e3,ζ1, ζ2, ζ3 is zero (white noise), and the scale of each dimension has been fixed (assumed to be a unit value λ11 = λ22 = λ33 = 1), then (5):
Therefore, to measure the true value3 of the factor g, it is advisable to fix its scale, meaning that one of the γ values must also be fixed. To do this, we choose one of the dimensions as the “best” or the one that best “measures” the factor g in this case. If, for example, we set γ10 = 1, then (6):
In this way, the observable indicator of the first dimension would be sufficient to estimate the true value of the factor g4.
Recall that, according to Edwards (2001), constructs with dimensions cannot be separated from their dimensions; that is, if we accept this conceptualization, we are saying that the factor g does not exist independently of its multidimensionality. An example of how to test this type of model (even third-order, with dimensions and higher-order factors at two levels) can be found in Martínez and Martínez (2008). However, these types of models are openly criticized by Hayduk et al. (1995), as detailed by Martínez and Martínez (2010a), who acknowledged the limitations of their earlier work from 2008.
As is well known, when performing factor analysis to test the model, the focus is on the covariance structure, not the means. However, this does not negate the fact that if the causal relationships of the model are specified (as presented in Figure I), the interpretation of the true value of each latent variable follows as we have explained. Thus, proposing a multidimensional model as shown on the left side of Figure I, which reflects an underlying factor g, implies that from a measurement perspective, the factor g can be measured with the “best” indicator of the “best” dimension, that is, with a single item. Moreover, (6) must be satisfied, meaning that with any item from the other dimensions, the true value of g could be determined just by estimating the respective parameter γ.
This is compatible, as it should be, with the reflective view of measurement, where the items of a latent variable can be considered interchangeable, indicating that removing an item does not alter the meaning of the latent variable. Variations in the latent variable manifest as variations in the items that measure them. Similarly, in a multidimensional construct, variations in the underlying dimension manifest as variations in its multiple dimensions; removing a dimension does not alter the meaning of the underlying construct.
It seems obvious that this interpretation is not what researchers in high abilities would want to propose, but it is what they imply when they use the factorial model. At this point, a different approach to measurement is needed, changing the causal relationship between the indicators and the latent variables towards formative models (Bollen & Lennox, 1991; Bollen & Diamantopoulos, 2017).
Formative indicators are not interchangeable and do not need to correlate. If one of these indicators is eliminated, the meaning of the latent variable is altered, as that variable is defined by those indicators. Thus, the latent variable is defined by the observable indicators (with nuances explained in Bollen & Diamantopoulos, 2017), meaning the definition of the latent variable depends on how its measurement is operationalized. It is a truly constructivist view, of great practical utility, that perfectly captures the objective of models proposing scales whose total value, formed from the aggregation of items, serves to discriminate between subjects who possess a certain trait to a greater or lesser extent.
The discussion on the types of formative measurement structures is beyond the scope of this work, as its characterization is very broad and can be consulted in Bollen and Diamantopoulos (2017). For the specific case of the GRS 2 scale analyzed by Tourón et al. (2023), it is perhaps more appropriate to refer to proposals such as that of Hayduk et al. (2019), illustrated in the “extended model” part of Figure I.
The indicator called f(yw) is a composite indicator of the items from the different dimensions y1, y2, y3 and their respective weights w1, w2, w3, i.e., it is a function of the observable indicators:
As it is a deterministic linear combination, there is no error term, so, as indicated in Figure I, ef = 0.
This conceptualization aligns much more with the approach of Tourón et al. (2023), who state:
“The development of the socio-emotional competence dimension was undertaken with the aim of broadening the assessment of the gifted beyond a traditional lens that focuses primarily on “head strengths” – which include problem solving, memory, reasoning and creativity – to a more holistic and comprehensive view of the student that includes “heart strengths” such as personal and interpersonal strengths (Pfeiffer, 2001, 2017b). Essentially, the purpose was to incorporate a positive psychology perspective into the GRS 2 parenting scale.”
Here, it is the researchers who define what high ability is based on the instrumentalization of the measurement. In simple terms, a new dimension is included because they believe that doing so better defines or evaluates the concept of high ability. Therefore, the evaluation of high ability depends on the dimensions chosen for its measurement, aligning with a formative view of measurement, not a reflective one. Thus, the characterization of high ability in an individual depends on the scores in the different dimensions. Those who score high in all dimensions, for example, will be considered to have greater ability than those who score high in only one dimension. Consequently, the value of the variable measured as general ability depends on the scores in all dimensions; a profile of each person’s ability is created based on their scores in each dimension and the combination of these.
The last part of the extended model in Figure I comprises the latent variables η4 and η5, which correspond to measurement scale effects and a control variable, respectively. The factorial model is expanded by considering a causal structure between latent variables, taking into account the effects of the high ability measurement scale and one (or more, if applicable) exogenous covariates that act as controls for those effects. This scheme is similar to the one proposed by Hayduk et al. (2019), so the approach described in that work can be used to test the GRS 2 model.
Analogy with High Physical Abilities
The model presented in Figure I, which represents an instrument for measuring high intellectual abilities, may be more understandable if we compare it to measuring high physical abilities.
Assume that η0 is a variable representing high physical ability, an elusive concept that is difficult to measure directly. A multidimensional conception is then proposed, involving other latent variables such as speed, strength, and aerobic endurance (Jung, 2022). These variables are measured using observable indicators (speed test, strength test, endurance test). This is a formative conceptualization, not a reflective one, for the following reasons:
- We are defining high physical ability based on these three dimensions that we consider. Another researcher could challenge this approach and add another dimension, such as flexibility (see Jung, 2022), which would change the definition of high physical ability.
- The dimensions considered do not have to be strongly associated. For example, individuals with more muscle mass and fast-twitch fibers are likely to excel in speed and strength but not necessarily in endurance.
- The dimensions are not interchangeable, and if one of them is removed, the meaning of the variable of interest (high physical ability) is altered.
- High physical ability cannot be measured through one indicator, as derived from the reflective conception of equation (6). It would be incorrect to estimate high physical ability with just one dimension; thus, all dimensions that define the concept of high physical ability are needed to “measure” it.
- Individuals who score high in all three dimensions will be considered to have greater physical ability than those who score high in one dimension but low in the other two.
Thus, a scale could be constructed with a weighting function specified by the researcher to form the overall index f(yw). This index could be causally related to consequence variables η5, such as the athlete’s performance on a football team, and control variables η4, such as sex or age.
These arguments, although simplistic, are didactic and help illustrate that the measurement of high intellectual abilities should follow a similar modeling approach.
Model Testing
Tourón et al. (2023) report the goodness of fit of their original model and the subsequent specifications they test (comparing the fit of eight competitive models), not using the chi-square test as a criterion5 (exact fit) and instead using a series of fit indices, including RMSEA, TLI, and others: “Following Hu and Bentler (1999), an acceptable fit in the combination of these indices is sufficient as evidence of validity”.
A few years after Hu and Bentler’s (1999) study, several works (Beauducel & Wittmann, 2005; Fan & Sivo, 2005; Marsh et al., 2004) questioned the use of fixed criteria or “golden rules” for the evaluation of models with “approximate” fit indices (CFI, TLI, SRMR, RMSEA, etc.) in response to the cut-off rules proposed by Hu and Bentler (1999). Other subsequent studies also critiqued these criteria (e.g., Niemand & Mai, 2018; McNeish & Wolf, 2023). These criteria are commonly used to adjust models to avoid the only suitable test for detecting model misspecification—the chi-square test or, more correctly, the family of chi-square tests—a test that tells us if the model is correct, it will not be rejected even with larger sample sizes (e.g., Hayduk & Glaser, 2000a, b; Barrett, 2007; Hayduk et al., 2007; McIntosh, 2007; Antonakis et al., 2010; McIntosh, 2012; Hayduk, 2014b; Ropovik, 2015; Rönkkö et al., 2016).
The degree of misfit in the covariance structure is not associated with the degree of misspecification (Hayduk, 2014b); thus, it is incorrect to identify statistical divergence from the proposed model as an indicator of its suitability. In structural equation models, one starts with a covariance matrix among the observable indicators. This matrix is compared with the covariance matrix implied by the model, which results from the causal constraints we are imposing. The matrix implied by the model is considered the population matrix because we stipulate that this model governs the population. Therefore, the specified model is the worldview we want to test against the data, which, except for sampling variability (hence the chi-square statistical test based on its degrees of freedom), must fit exactly.
The chi-square test can sometimes fail to detect misspecified models. For example, the possible existence of equivalent models (same fit but with different causal constraints) is well known. Hence, theoretical commitment to the model is crucial for choosing among models that fit, selecting the one congruent with the supporting theory. Nevertheless, despite this limitation, it remains the only possible analysis path, better than the other indices commonly reported, which almost always cite Hu and Bentler (1999), as Hayduk (2014a) explains.
Thus, when a model does not pass the chi-square test, the estimated parameters are not interpretable, as one or more of the covariance relationships implied by the model are not supported by the empirical data, which immediately biases the estimates. Consequently, it also makes no sense to interpret indices like composite reliability or average variance extracted. Conversely, if the model fits, then the possibility of competitive models (alternative theories) and/or equivalent models that can also fit must be considered. The one with the best fit should be chosen in the case of competing models (via the chi-square difference test between two competitive models that fit) or the one that is theoretically grounded in the case of equivalent models (in line with the conception of causality from qualitative assertions stipulated by Pearl, 2000).
As derived from the previous discussion, this approach is much more demanding with the models proposed, especially in social sciences, where there is a kind of “automatic writing” in research (Martínez & Martínez, 2009). Errors and inaccuracies are systematically reproduced, making these errors the majority position. This majority position, simply by being prevalent, continues to encourage others to adopt it. Hayduk (2014b) illustrates this fact with an anecdote in which one of the creators of the software that was, for many years, the most used in this methodology (LISREL), admitted that, since the chi-square test rejected many models, they had to propose other fit indices (GFI, AGFI, etc.) that were less demanding with the data to have fewer rejected models, satisfy researchers, and thus make the software more accepted.
Factor Analysis
Tourón et al. (2023) employ exploratory and confirmatory factor analysis: “In order to test the structure of the scale, an exploratory and a confirmatory factor analysis were carried out to provide evidence of the validity of the scale”.
Hayduk (2014b) demonstrates that exploratory factor analysis is incapable of detecting the true structure of the data, that is, identifying the model that generated the empirical data. Therefore, a theoretical model cannot be tested with exploratory analysis; it only provides a view of the correlational structure of the data.
Tourón et al. (2023) make a commendable effort by dividing the sample into two parts. They use exploratory factor analysis on the first 40% of the sample and test the structure of the four factors found in the exploratory phase on the remaining 60%. Methodologically, partitioning the data in this way is laudable, although it would have been more effective to use the same partitions differently. In the first part, the original three-factor structure could have been tested using confirmatory factor analysis, studying possible causes of misfit (analyzing, for example, modification indices as long as they are theoretically supported). If, after analyzing the modification indices, a different specification that fits via chi-square had been recommended, then this new specification could have been tested with a new confirmatory factor analysis on the remaining 60% of the sample.
This proposal, however, is far from optimal (though better than performing exploratory factor analysis, as it is more consistent with any hypothetico-deductive method that aims to test the structure of a scale). Although the chi-square test is more effective than identifying eigenvalues in exploratory factor analysis (Hayduk, 2014b), it can sometimes fail to identify the correct model. Consequently, the need arises to analyze construct validity through the construction of a network of causes and/or effects of the latent variables whose validity is being studied. This approach involves postulating a nomological network, as advocated by Cronbach and Meehl (1955).
As Hayduk (2014b) recalls, testing the construct within the nomological network questions the ability of the latent factor to produce its observable indicators, which is indispensable for discussing construct validity (Cronbach & Meehl, 1955). Thus, in any study that aims to validate a measurement instrument, an “extended model” must be included, according to the terminology we have used in Figure I. This means going beyond factor analysis and incorporating the construct or constructs of interest into a nomological network. This is when structural equation models reach their full potential, allowing the testing of that model against empirical data, specifically, the covariance matrix implied by the model’s causal constraints against the covariance matrix of the observable indicators.
There are numerous criticisms of a procedure in psychometrics that, despite being widespread, is not correct. This procedure involves trying to validate a measurement instrument with exploratory factor analysis (even if confirmatory factor analysis is later performed) or with confirmatory factor analysis alone (even if the causal model is then tested, known as the “two-step analysis”). The fundamental reason for these criticisms is related to the concept of construct validity, as explained by Cronbach and Meehl (1955); measurement cannot be separated from theory, and construct validity requires a nomological network to be analyzed. Examples of these criticisms can be found in Fornell and Yi (1992), Hayduk and Glasser (2000a), and Hayduk (2014b).
Number of Items per Latent Variable
Tourón et al. (2023) translated the 20 original items of the GRS 2 scale for parents, grouping them into the three mentioned dimensions (6, 7, and 7 items, respectively). Since Tourón et al. (2023) do not provide the wording of the items, it is very complex to assess their suitability for reflecting the underlying dimensions. Nevertheless, at this point in the manuscript, we already know that in a reflective model, the true value of each latent dimension can be estimated from the value of each observable indicator. According to the specification of Tourón et al. (2023), the observable indicators are reflective, so each of these dimensions could, theoretically, be measured with just one indicator. If a researcher believes that a single indicator is insufficient to measure a latent variable and needs more because the latent dimension is broad (as indicated by Tourón et al. (2023)), it is likely that this battery of indicators is measuring different latent variables. In other words, they are not manifestations of a single latent variable, but several.
Using only one indicator per latent variable in Figure I is not just a way to simplify the scheme but also reflects research that supports single-item measures for latent variables when the latent variable manifests through reflective observables (e.g., Bergkvist & Rossiter, 2007; Matthews et al., 2022; Allen & Pistone, 2023; Wulf et al., 2023). As Durvasula et al. (2012) indicate, there is literature suggesting that long scales threaten construct validity and cause respondent fatigue. Moreover, when the same Likert scale format is used—that is, the same range for a large battery of items—there is a serious risk of common method bias (Jordan & Troth, 2020). One manifestation of this bias may be what Tourón et al. (2023) consider positive when they refer to the high correlations between each item and the rest, indicating the “uniformity of the set of items”. Furthermore, there are examples in the literature on high abilities and GRS scales where a halo effect, which obviously affects validity, can be observed (e.g., Jabůrek et al., 2020).
An exhaustive explanation of the need to use a single item (the best possible indicator) or, in certain cases, a second item to accompany the best indicator can be found in Hayduk (1996) and Hayduk and Littvay (2012). In the context of structural equations, Hayduk (1996) also proposes fixing the error variance of that best indicator, making the researcher commit to the meaning of the latent variable. This approach avoids interpretational confounding, which is the change in the relationship between the latent variable and its best indicator whenever the covariance structure of the data changes with the addition of other variables in the model.
Thus, in Figure I, it would be necessary not only to fix all the λs (which we have said is essential for scaling each latent variable) but also the error variances of each indicator, usually to a very small percentage of what would be the variance of the observable item. The model represented in Figure I could be expanded to include two items per latent variable. In fact, this would add robustness to the conceptualization because the second item (the second-best possible indicator) would not have its factor loading or error variance fixed. As a result, the new covariances added to the sample covariance matrix would provide a more solid test of the constraints produced by fixing the factor loading and error variance of those best indicators.
As Hayduk and Littvay (2012) explain, if the indicators are reflective, it is not advisable to use too many items per latent variable because this saturates the latent part of the model with factorial correlations. If a large number of items per latent variable are needed because the theoretical domain of the variable is broad, it is most likely that either several latent variables are being measured, or a formative structure is being envisioned instead of a reflective one.
Alternative Models
There are other model specifications compatible with all the previous arguments, which are different from Figure I, as shown in Figures II, III, and IV.
FIGURE II. Alternative Model without a Global Scale
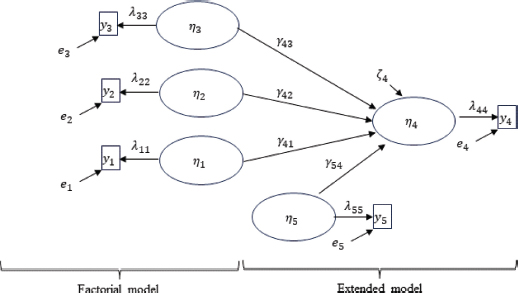
FIGURE III. Alternative Model without a Global Scale and with Causes of Dimensions
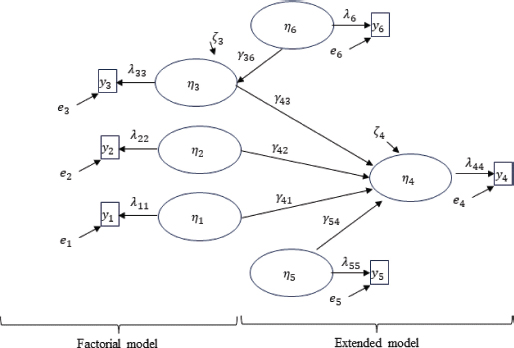
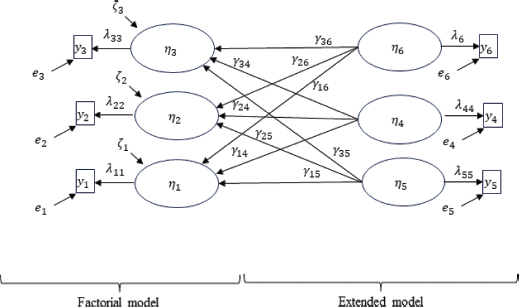
FIGURE IV. Alternative Model with Causes of the High Abilities Dimensions
In Figure II, a model similar to Figure I is represented, except that there is no attempt to construct a global index that measures ability as a function of the dimensions. Instead, the theory is more prudent and admits that there are dimensions η1, η2, and η3 that can be measured reflectively with y1, y2, and y3, associated with high abilities, although the specific type of functional relationship is not specified (hence it is a more conservative specification). These dimensions influence a consequential variable η5 (for example, some performance variable, as specified by Kelly and Peverly, 1992), whose effect can be measured through the coefficients γ, and there is a control variable η4 (or several, although for simplicity only one is proposed) that could be, for example, some socioeconomic or demographic variable.
In Figure III, the model proposed in Figure II is further expanded, making it even more interesting from a causal perspective because it includes a variable η6 that can cause variation in one of the dimensions, such as the family context on creativity (Manzano & Arranz, 2008).
In Figure IV, possible causes of the dimensions of high abilities are shown instead of their consequences. This scheme is (with nuances) equivalent to the one used by Pfeiffer et al. (2008) to validate the GRS-S scale, proposing variables that can cause variation in the dimensions they use (six instead of the three in Figure IV), where the exogenous latent variables η4, η5 and η6 are gender, race, and age. Evidently, they do this using another statistical methodology (multigroup analysis of variance), but the causal diagram is equivalent to the one shown in Figure IV. To test the hypothesis stipulated by Pfeiffer et al. (2008) that the GRS-S scale should not discriminate between gender, race, and age, in a structural equation model, all γ parameters would simply need to be fixed to zero, and these causal restrictions tested with the chi-square test. Remember that structural equation models allow the use of dichotomous exogenous variables and that any variable is susceptible to being considered latent due to measurement error. For example, sex or age may have coding errors, so the error variance of their indicators can be fixed not necessarily to zero.
It should be noted that Pfeiffer et al. (2008) do not use a single item to measure each dimension but several (12 for each of the 6 dimensions), so the criticisms made in this manuscript regarding the confusion between reflective and formative indicators and what this implies for modeling would be applicable.
Therefore, any of the modeling proposals expressed in Figures II, III, and IV would have helped Tourón et al. (2023) to more rigorously analyze the construct validity of their adaptation of the GRS 2 scale to the Spanish context.
Discussion
The study by Tourón et al. (2023), while making a commendable procedural effort to analyze the construct validity of the GRS 2 scale for parents in the Spanish context, lacks essential elements that question its validity.
The first issue relates to the specification of a reflective model instead of a formative one. Tourón et al. (2023) consider both the items of each dimension and the dimensions themselves as reflective (Edwards, 2001). They specify them in the causal relationship between the latent variables and their respective items, and in the relationship between second-order factors and dimensions. Although the authors do not show the complete battery of items in their article, they do mention some of them, such as items 5, 8, and 15, which they place as manifestations of the dimension (ultimately identified as a subdimension) “emotional control.” These items refer to stress control, anger, and perseverance at work, suggesting that they are indicators of different latent variables or that they should be causes and not effects of the variable labeled (constructed and defined based on its indicators) “emotional control.” Constructing summative scales with the items of each dimension or a single global scale to provide a profile of each individual’s ability represents a formative view. This analysis perspective is shown in Figure I and requires the addition of other variables related to the constructed scale or scales to the factorial structure. This formative view aligns with Boring’s (1923) perspective on intelligence and the tests to measure it6.
The second problematic aspect of the study by Tourón et al. (2023) is the failure to acknowledge that all the models tested (eight in total) are incompatible with the empirical data and, therefore, incorrect, i.e., not valid. It is true that in the specialized literature on structural equations, some researchers (e.g., Jöreskog, 1978; Bentler, 1990; Steiger, 2007; Browne et al., 2002) criticize the chi-square test and recommend approximate fit indices. Interestingly, Jöreskog, Bentler, Steiger, and Browne were creators of commercial structural equation software (LISREL, EQS, SEPATH, and RAMONA, respectively). Other researchers follow the same line (e.g., McNeish & Wolf, 2023).
However, the main criticisms of the exact fit test are addressed one by one by Hayduk (2014b). One of the most recurrent criticisms is the mantra that “all models are wrong,” suggesting it would not make sense to seek an exact fit. Although Hayduk (2014b) responds to this criticism, it is worth consulting sources outside the field of structural equations for a more general perspective on probability theory, data modeling, and statistical inference (e.g., Spanos, 2019).
Spanos (2021) reminds us that there is a misinterpretation of this “mantra” since one must distinguish between a substantive model (based on a theory) and the statistical model implicit in it, which encompasses a set of probabilistic assumptions imposed on the data. Researchers who claim that “all models are wrong” attempt to justify the inevitability of statistical misspecification and, therefore, argue that seeking an exact fit is pointless. However, this is incorrect because the motto refers to substantive models that are, understandably, a simplified representation of reality.
What is tested via chi-square in structural equation models is not whether the substantive model is “true,” but whether the implicit statistical model is congruent with the empirical data, which includes causal constraints and probabilistic assumptions. Hence the importance of theory in constructing a causal model and the need to be rigorous in respecting the evidence marked by the discrepancy between the proposed model and the empirical data when the model’s assumptions are met, as Spanos (2019) generally explains in data modeling.
This inevitably leads us to the third element of criticism of Tourón et al. (2023), which relates to the use of factor analysis for the study of construct validity and the need to stipulate a nomological network that can be globally tested. It is true that, as indicated in Lissitz (2009), there are also proposals for abandoning the validation processes recommended by Cronbach and Meehl (1955) and focusing on an ontological perspective, as defended by Borsboom et al. (2004): a test is valid for measuring an attribute if and only if (a) the attribute exists and (b) variations in the attribute causally produce variations in the measurement outcomes. However, the theses of Hayduk (1996) and Borsboom et al. (2004) share more than they differ, as analyzed by Martínez and Martínez (2009), so there should be no substantial disagreements with the arguments presented in this work.
The number of items per latent variable is the fourth criticism of Tourón et al. (2023). Although, as previously mentioned, it is likely that several items of the GRS 2 instrument are formative, if they are stipulated as reflective, there is no need to saturate the instrument with so many items that can cause different types of bias. However, if researchers argue that all those items are necessary due to the breadth of the measured concepts and because they are needed to capture the characteristics of what is being measured, then they are implicitly admitting a formative, not reflective, structure.
Additionally, we have proposed various models that follow the same philosophy shown in Figure I, which would address the limitations of the proposal by Tourón et al. (2023). These models are not unique, as other proposals in high abilities research already venture into similar specifications, such as Nakano et al. (2016) and their MIMIC model (multiple causes and multiple indicators). Furthermore, as we have indicated, Pfeiffer et al. (2008) use a similar (although not as statistically rigorous) method for validating the GRS-S scale as specified in Figure IV.
In the models in Figures II, III, and IV, it is not explicitly stated that there is a higher-order ability factor manifested through dimensions. An attractive future research direction would be to take a network approach similar to that used in psychopathology (Borsboom & Cramer, 2013; Fonseca-Pedrero, 2017), considering these ability dimensions as “symptoms” that interact complexly in a network. None of the conceptions we have proposed are incompatible with this view since the correlations between these ability dimensions are left free.
The modeling examples shown in Figures I to IV are just references. They must be adapted to the set of latent variables in each context. However, it is important to specify clearly what is being measured and what variable is considered a type of endowment or not. Tourón et al. (2023) indicate that socio-emotional skills are not seen as a type of giftedness. Therefore, when explaining what multidimensionality means in high abilities and specifying it in a model, that distinction must be clear.
It would also be important to discuss other criticisms of the GRS 2 measurement instrument, though they would exceed the scope of this work, such as the use of ordinal Likert-type scales with linguistic labels, given potential interactions between these labels and the numerical scale. Approaches based on fuzzy logic could offer insights into the appropriateness of such scales (see Martínez & Martínez, 2010b; Martínez et al., 2010). Moreover, reporting mean values as Tourón et al. (2023) do with ordinal scales is at least questionable (Liddell & Kruschke, 2018).
Lastly, since Tourón et al. (2023) acknowledge that their study is a preliminary validation and should be validated further with subsequent research, we recommend considering the arguments presented in this manuscript to advance further in the measurement of high abilities.
References
Allen, B., & Pistone, L. F. (2023). Psychometric evaluation of a single-item screening tool for the presence of problematic sexual behavior among preteen children. Child abuse & neglect, 143, 106327. https://doi.org/10.1016/j.chiabu.2023.106327
Antonakis, J., Bendahan, S., Jacquart, P., Lalive, R. (2010). On making causal claims: A review and recommendations. Leadership Quarterly, 21, 1086-1120. https://doi.org/10.1016/j.leaqua.2010.10.010
Barret P. (2007). Structural equation modelling: Adjudging model fit. Personality and Individual Differences, 42(5), 815-824. https://doi.org/10.1016/j.paid.2006.09.018
Beauducel, A., & Wittmann, W. W. (2005). Simulation Study on Fit Indexes in CFA Based on Data with Slightly Distorted Simple Structure. Structural Equation Modeling, 12(1), 41–75. https://doi.org/10.1207/s15328007sem1201_3
Bentler, P. M. (1990). Comparative fit indexes in structural models. Psychological Bulletin, 107(2), 238–246. doi:https://doi.org/10.1037/0033-2909.107.2.238
Bergkvist, L. , & Rossiter, J. R. (2007). The predictive validity of multiple-item versus single-item measures of the same constructs. Journal of Marketing Research, 44 (2), 175-184 https://doi.org/10.1509/jmkr.44.2.175
Bollen, K., & Lennox, R. (1991). Conventional wisdom on measurement: A structural equation perspective. Psychological Bulletin, 110(2), 305–314. https://doi.org/10.1037/0033-2909.110.2.305
Bollen K. A. (2002). Latent variables in psychology and the social sciences. Annual review of psychology, 53, 605–634. https://doi.org/10.1146/annurev.psych.53.100901.135239
Bollen, K. A., & Diamantopoulos, A. (2017). In defense of causal-formative indicators: A minority report. Psychological Methods, 22(3), 581–596. https://doi.org/10.1037/met0000056
Boring, E. G. (1923). Intelligence as the test measures it. The New Republic, 35, 35-37.
Borsboom, D., & Cramer, A. O. (2013). Network analysis: an integrative approach to the structure of psychopathology. Annual Review of Clinical Psychology, 9, 91–121.
Borsboom, D., Mellenbergh, G. J., van Heerden, J. (2004). The concept of validity. Psychological Review, 111(4), 1061-1071.
Browne, M. W., MacCallum, R. C., Kim, C. T., Andersen, B. L., Glaser, R. (2002). When fit indices and residuals are incompatible. Psychological Methods, 7(4), 403–421. https://doi.org/10.1037//1082-989x.7.4.403
Cronbach, L. J., & Meehl, P. E. (1955). Construct validity in psychological test. Pyschological Bulletin, 52, 218-302. https://doi.org/10.1037/h0040957
Durvasula, S., Sharma, S., Carter, K. (2012). Correcting the t statistic for measurement error. Marketing Letters, 23(3), 671–682. doi:https://doi.org/10.1007/s11002-012-9170-9
Edwards, J. R. (2001). Multidimensional constructs in organizational behavior research: Towards an integrative and analytical framework. Organizational Research Methods, 4, 144–192.
Fan, X., & Sivo, S. A. (2005). Sensitivity of fit indexes to misspecified structural or measurement model components: Rationale of two-index strategy revisited. Structural Equation Modeling, 12, 334-367. doi:https://doi.org/10.1207/s15328007sem1203_1
Fonseca-Pedrero, E. (2017). Análisis de redes: ¿una nueva forma de comprender la psicopatología? Revista de Psiquiatría y Salud Mental, 10(4), 206-215.
Fornell, C. & Yi, Y. (1992). Assumptions of the Two-Step Approach to Latent Variable Modeling. Sociological Methods & Research 20, 291-320.
Hayduk, L. A. (1996). LISREL Issues, Debates and Strategies. Baltimore, MD: Johns Hopkins University Press.
Hayduk, L. A. (2014a). Seeing perfectly fitting factor models that are causally misspecified: Understanding that close-fitting models can be worse. Educational and Psychological Measurement, 74(6), 905-926. https://doi.org/10.1177/0013164414527449
Hayduk, L. A. (2014b). Shame for disrespecting evidence: The personal consequences of insufficient respect for structural equation model testing. BMC: Medical Research Methodology, 14, 124 https://doi.org/10.1186/1471-2288-14-124
Hayduk, L. A., Cummings, G. Boadu, K., Pazderka-Robinson, H., & Boulianne, S. (2007). Testing! testing! one, two, three – Testing the theory in structural equation models! Personality and Individual Differences, 42(5), 841-850.
Hayduk, L. A., Estabrooks, C. A., Hoben, M. (2019). Fusion Validity: Theory-Based Scale Assessment via Causal Structural Equation Modeling. Frontiers in Psychology, 10, 1139. https://doi.org/10.3389/fpsyg.2019.01139
Hayduk, L. A., & Glaser, D. N. (2000a). Jiving the four-step, waltzing around factor analysis, and other serious fun. Structural Equation Modeling, 7(1), 1-35.
Hayduk, L. A., & Glaser, D. N. (2000b). Doing the four-step, right-2-3, wrong-2-3: A brief reply to Mulaik and Millsap; Bollen; Bentler; and Herting and Costner. Structural Equation Modeling, 7(1), 111-123.
Hayduk, L. A., & Littvay, L. (2012). Should researchers use single indicators, best indicators, or multiple indicators in structural equation models? BMC Medical Research Methodology, 12, 159, 1-17. https://doi.org/10.1186/1471-2288-12-159
Hayduk, L. A., Ratner, P. A., Johnson, J. L., Bottorff, J. L. (1995). Attitudes, ideology and the factor model. Political Psychology, 16, 479–507.
Hu, L. T., & Bentler, P. M. (1999). Cutoff Criteria for Fit Indexes in Covariance Structure Analysis: Conventional Criteria versus New Alternatives. Structural Equation Modeling, 6(1), 1–55. https://doi.org/10.1080/10705519909540118
Jabůrek, M., Ťápal, A., Portešová, Š., Pfeiffer, S. I. (2020). Validity and Reliability of Gifted Rating Scales-School Form in Sample of Teachers and Parents – A Czech Contribution. Journal of Psychoeducational Assessment, 39(3), 361–371. https://doi.org/10.1177/0734282920970718
Jordan, P. J., & Troth, A. C. (2020). Common method bias in applied settings: The dilemma of researching in organizations. Australian Journal of Management, 45(1), 3-14. https://doi.org/10.1177/0312896219871976
Jöreskog, K. G. (1978). Structural analysis of covariance and correlation matrices. Psychometrika, 43, 443-477.
Jung J. Y. (2022). Physical giftedness/talent: A systematic review of the literature on identification and development. Frontiers in Psychology, 13, 961624. https://doi.org/10.3389/fpsyg.2022.961624
Kelly, M. S. & Peverly, S. T. (1992). Identifying bright kindergartners at risk for learning difficulties: Predictive validity of a kindergarten screening tool. Journal of School Psychology, 30, 245-258.
Liddell, T. M. & Kruschke, J. K. (2018). Analyzing ordinal data with metric models: What could possibly go wrong? Journal of Experimental Social Psychology, 79, 328-348. https://doi.org/10.1016/j.jesp.2018.08.009
Lissitz, R. W. (Editor) (2009). The Concept of Validity: Revisions, New Directions, and Applications. Charlotte, NC: Information Age Publishing.
MacCallum, R. C., & Austin, J. T. (2000). Applications of Structural Equation Modeling in Psychological Research. Annual Review of Psychology, 51, 201-226. https://doi.org/10.1146/annurev.psych.51.1.201
Manzano, A. Arranz, F., Enrique B. (2008). Contexto familiar, superdotación, talento y altas capacidades». Anuario de psicología / The UB Journal of psychology, 39(3), 289-309, https://raco.cat/index.php/AnuarioPsicologia/article/view/123643
Marsh, H. W., Hau, K. T., Wen, Z. (2004). In search of golden rules: Comment of hypothesis-testing approaches to setting cutoff values for fit indexes and dangers in overgeneralizing Hu and Bentler’s (1999) findings. Structural Equation Modeling, 11, 320-341. https://doi.org/10.1207/s15328007sem1103_2
Martínez, J. A., Ko, Y. J., & Martínez, L. (2010). An application of fuzzy logic to service quality research: A case of fitness service. Journal of Sport Management, 24, 502-523. https://doi.org/10.1123/jsm.24.5.502
Martínez, J. A. & Martínez, L. (2009). El análisis factorial confirmatorio y la validez de escalas en modelos causales. Anales de Psicología, 25(2), 368-374
Martínez, J. A. & Martínez, L. (2010). Re-thinking perceived service quality. An alternative to hierarchical and multidimensional models. Total Quality Management & Business Excellence, 21 (1), 93-118
Martínez, J. A. & Martínez, L. (2010). La medición de la satisfacción de servicios deportivos a través de la lógica borrosa. Revista de Psicología del Deporte, 19(1), 41-58
Martínez, L., & Martínez, J. A. (2008). Developing a multidimensional and hierarchical service quality model for the travel agencies industry. Tourism Management, 29, 706–720.
Matthews, R. A., Pineault, L. & Hong, Y. H. (2022). Normalizing the use of single-item measures: Validation of the single item compendium for organizational psychology. Journal of Business and Psychology, 37, 639-673. https://doi.org/10.1007/s10869-022-09813-3
McIntosh, C. N. (2007). Rethinking fit assessment in structural equation modelling: A commentary and elaboration on Barrett (2007). Personality and Individual Differences, 42(5), 859–867. https://doi.org/10.1016/j.paid.2006.09.020
McIntosh, C. N. (2012). Improving the evaluation of model fit in confirmatory factor analysis: A commentary on Gundy, CM, Fayers, PM, Groenvold, M., Petersen, M. Aa., Scott, NW, Sprangers, MAJ, Velikov, G., Aaronson, NK (2011). Comparing higher-order models for the EORTC QLQ-C30. Quality of Life Research. Quality of Life Research, 21(9), 1619- 1621.
McNeish, D., & Wolf, M. G. (2023). Dynamic fit index cutoffs for confirmatory factor analysis models. Psychological Methods, 28(1), 61–88. https://doi.org/10.1037/met0000425
Nakano, T. D., Primi, R., Ribeiro, W. D., Almeida, L.D. (2016). Multidimensional Assessment of Giftedness: criterion Validity of Battery of Intelligence and Creativity Measures in Predicting Arts and Academic Talents. Anales De Psicologia, 32, 628-637.
Niemand, T. & Mai, R. (2018). Flexible Cutoff Values for Fit Indices in the Evaluation of Structural Equation Models. Journal of the Academy of Marketing Science, 46(6), 1148-1172.
Pearl, J. (2000). Causality: Models, reasoning, and inference. Cambridge University Press.
Pfeiffer, S. I., Petscher, Y., & Kumtepe, A. (2008). The Gifted Rating Scales-School Form: A Validation Study Based on Age, Gender, and Race. Roeper review, 30(2), 140–146. https://doi.org/10.1080/02783190801955418
Rönkkö, M., McIntosh, C. N., Antonakis, J., Edwards, J. R. (2016). Partial least squares path modeling: Time for some serious second thoughts. Journal of Operations Management. 47–48, 9–27. https://doi.org/10.1016/j.jom.2016.05.002
Ropovik, I. (2015). A cautionary note on testing latent variable models. Frontiers in Psychology, 6. https://doi.org/10.3389/fpsyg.2015.01715
Sofologi, M., Papantoniou, G., Avgita, T., Lyraki, A., Thomaidou, C., Zaragas, H., Ntritsos, G., Varsamis, P., Staikopoulos, K., Kougioumtzis, G., Papantoniou, A., & Moraitou, D. (2022). The Gifted Rating Scales-Preschool/Kindergarten Form (GRS-P): A Preliminary Examination of Their Psychometric Properties in Two Greek Samples. Diagnostics (Basel, Switzerland), 12(11), 2809. https://doi.org/10.3390/diagnostics12112809
Spanos. A. (2019). Probability Theory and Statistical Inference: Empirical Modeling with Observational Data, Cambridge University Press, Cambridge
Spanos, A. (2021). Modeling vs. inference in frequentist statistics: ensuring the tustworthiness of empirical evidence. Descargado desde: https://errorstatistics.files.wordpress.com/2021/03/modeling-vs-inference-3-2021.pdf
Steiger, J. H. (2007). Understanding the limitations of global fit assessment in structural equation modelling. Personality and Individual Differences. 42(5), 893-898
Tourón, M., Navarro-Asensio, E., Tourón, J. (2023). Validez de Constructo de la Escala de Detección de alumnos con Altas Capacidades para Padres, (GRS 2), en España. Revista de Educación, 1(402), 55-83. https://doi.org/10.4438/1988-592X-RE-2023-402-595
Wulf, J. N., Sajons, G. B., Pogrebna, G. et al. (2023). Common methodological mistakes. The Leadership Quarterly, 34(1), 101677, https://doi.org/10.1016/j.leaqua.2023.101677
Contact information: José A. Martínez García, Universidad Politécnica de Cartagena. Facultad de Ciencias de la Empresa. Departamento de Economía de la Empresa. Calle Real, 3, 3021, Cartagena. E-mail: josean.martinez@upct.es
_______________________________
1 It is not the objective of this work to discuss the various conceptualizations of high abilities. It is evident that the literature is extensive on this subject, and there is discussion about the definition, policies, and practices, as highlighted by McClain and Pfeiffer (2012). We will simply consider that high abilities are conceived as a multidimensional variable or as a variable that cannot be directly measured and manifests through different dimensions or traits.
2 It is evident that if the data are parameterized as deviations from the mean, the “true” mean value of each latent variable is zero.
3 We emphasize that we are not necessarily admitting that a “true value” of the g factor can be measured, but rather we are simply using the same jargon that is used in the context of latent variables in this type of modeling. The important aspect is what the equations represent in terms of relating the variables of the model, regardless of whether a specific numerical value makes sense or not, especially when measurement scales are arbitrary. Thus, what is being questioned is the model itself through the analysis of the equations that represent it.
4 If the scale were not fixed, the interpretation would be identical, this time simply that the true value of g would be weighted by a causal coefficient between g and the relevant dimension, but it would still suffice to have a single observable for each dimension to calculate that value of g.
5 Note that the reported value of chi-square divided by the degrees of freedom is not a statistical test.
6 Again, we do not intend to engage in a deeper discussion on the concepts of intelligence, ability, etc. We only argue that a formative view would tell us that what we are measuring is determined by how we have defined it beforehand. Therefore, the key lies in how the concept to be measured is defined.