Crítica del análisis de la validez de constructo de la Escala de Detección de alumnos con Altas Capacidades para Padres (GRS 2); réplica a Tourón et al. (2023)
criticism of the analysis of Construct Validity of the Gifted Rating Scales (GRS 2) Parent Form in Spain; a reply to Tourón et al. (2023)
https://doi.org/10.4438/1988-592X-RE-2024-406-649
José A. Martínez García
https://orcid.org/0000-0003-2131-9101
Universidad Politécnica de Cartagena
Resumen
El objetivo de este trabajo es reexaminar los métodos de análisis de la validez de constructo de la escala de detección de alumnos con altas capacidades para padres (GRS 2) en España, realizados por Tourón et al. (2023). Para ello, partimos de la propuesta de estos autores, criticando de forma constructiva algunos de sus procedimientos, y planteando alternativas de modelización y análisis. De este modo, se emplea un enfoque eminentemente didáctico, basado fundamentalmente en la literatura sobre modelos de ecuaciones estructurales y psicometría. La distinción entre modelos reflectivos y formativos, la dirección de causalidad y las ecuaciones subyacentes, la idoneidad de analizar la validez de constructo en una red nomológica yendo más allá del análisis factorial, y el test del modelo estructural usando la chi-cuadrado, son los principales ejes sobre los que se articula la crítica. Asimismo, se proponen diferentes opciones de modelización que son congruentes con líneas de investigación en medición de altas capacidades, y que podrán servir de base para seguir avanzando en esta disciplina en el futuro.
Palabras clave: escala de detección, altas capacidades, validez de constructo, análisis factorial confirmatorio, ecuaciones estructurales, modelos formativos.
Abstract
The objective of this study is to reexamine the methods used to analyze the construct validity of the Gifted Rating Scales (GRS 2) Parent Form in Spain, originally conducted by Tourón et al. (2023). To achieve this, we build upon the proposals of these authors, offering constructive criticism of some of their procedures and suggesting alternative modeling and analysis methods. Our approach is primarily didactic, drawing extensively from the literature on structural equation modeling and psychometrics. Key elements of our critique include the distinction between reflective and formative models, the direction of causality and the underlying equations, the appropriateness of analyzing construct validity within a nomological network beyond factor analysis, and the use of chi-square testing for the structural model. Additionally, we propose various modeling options that align with current research trends in the measurement of high abilities, providing a foundation for future advancements in this discipline.
Keywords: gifted rating scales, high ability, construct validity, confirmatory factor analysis, structural equation modeling, formative models.
Introducción
La investigación de Tourón et al. (2023) analizó la validez de constructo de la Escala de Padres de las GRS 2 (Gifted Rating Scales) en España, sobre una muestra final de 1109 padres y madres de niños y adolescentes (entre 4 y 18 años) con altas capacidades. Esta escala, basada en un modelo original de 3 dimensiones (capacidades cognitivas, capacidades creativas y artísticas, y habilidades socioemocionales) consta de 20 ítems repartidos en ellas. Tourón et al. (2023) adaptaron el cuestionario al español y procedieron al estudio de validación, obteniendo al final 4 factores: capacidad cognitiva, capacidad creativa, habilidades sociales y control emocional, agrupados dos a dos en sendos factores de orden superior: capacidad cognitivo-creativa y habilidades socio-emocionales, respectivamente.
Sin embargo, varios de los procedimientos metodológicos y de análisis de resultados descritos por Tourón et al. (2023) son cuestionables. Tanto el modelo factorial propuesto, basado en una visión reflectiva de la medición de las altas capacidades, como los índices de ajuste empleados para validar la estructura dimensional, de carácter aproximado, limitan seriamente la interpretación de los resultados.
El objetivo de este trabajo es reexaminar los métodos de análisis de la escala GRS 2. Para ello, partimos de la propuesta de Tourón et al. (2023), criticando de forma constructiva algunos de sus procedimientos, y planteando alternativas de modelización y análisis. Así, nuestra propuesta no solo discute la idoneidad del enfoque de Tourón et al. (2023), sino que puede servir como estímulo para replantear algunos de los procedimientos de modelización y análisis que se realizan en la investigación sobre altas capacidades.
Para conseguir tal fin, vamos a emplear un enfoque eminentemente didáctico, basado fundamentalmente en la literatura sobre modelos de ecuaciones estructurales y psicometría. Dividiremos las críticas en varios puntos fundamentales a desarrollar en los siguientes apartados.
Modelización reflectiva frente a formativa
Vamos a considerar el modelo presentado en la Figura I como base. En ese modelo, hay un vector de variables latentes η cuyo valor verdadero (true score) es desconocido, pero que podemos intentar conocerlo a través de la relación de estas variables latentes con un vector de indicadores observables y.
FIGURA I. Modelo factorial y modelo extendido
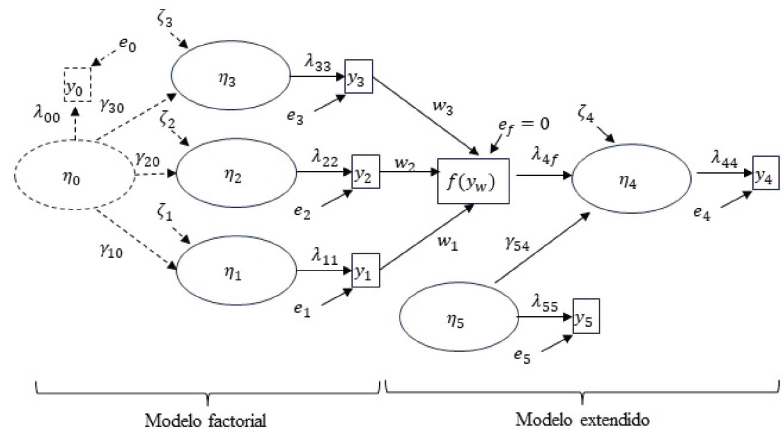
La parte llamada “factorial” pretende representar la conceptualización inicial de Tourón et al. (2023); existe un modelo multidimensional de las altas capacidades: capacidades cognitivas, capacidades creativas y artísticas, y habilidades socioemocionales. En la Figura I este modelo está representado por las variables latentes η1, η2, η3 y los indicadores observables (ítems) y1, y2, y3. Recordemos que, según MacCallum y Austin (2000) las variables latentes son constructos hipotéticos que no pueden ser directamente medidos. Es decir, se reflejan a través de una serie de indicadores observables que, como revela Bollen (2002), son localmente independientes y definen el valor esperado de la variable latente, la cual es una función no determinista de esos indicadores.
En aras de simplificar, la Figura I solo contiene un indicador por variable latente, en lugar de los 6, 7 y 7, respectivamente, del modelo GRS 2. Esta divergencia no afecta a nuestra exposición inicial, aunque será importante más adelante. La relación entre las variables latentes y sus indicadores es causal, en línea con la teoría clásica de los test: la variación en la variable latente η1 se manifiesta en una variación en el indicador observable, escalada con el parámetro λ11, a lo que hay que añadir un error aleatorio e1. Si los datos se parametrizan como desviaciones en torno a la media de los indicadores observables (algo habitual en programas informáticos especializados en este tipo de análisis, y que no afecta a las estructuras de covarianza), las ecuaciones que relacionan variables latentes e indicadores son tan sencillas como (1), representando la primera de las dimensiones:
Este tipo de estructura causal entre variables latentes e indicadores se denomina reflectiva (Bollen y Diamantopoulos, 2017), y los indicadores son manifestaciones (efectos) de la variable latente. Variaciones en el rasgo o factor latente producen variaciones en el indicador observable, en función de la elección (o estimación, según el caso) del factor de escala λ y del error e. La variable latente se escala con uno de sus indicadores (en este caso con el único indicador que tiene), fijando su valor (normalmente a la unidad, pero no necesariamente siempre así), lo que indica que variaciones unitarias en la variable latente se reflejan en variaciones también unitarias del indicador observable (más fluctuaciones aleatorias).
La parte “factorial” de la Figura I la completa la variable latente η0, que puede representar varios estados del mundo real. En primer lugar, se puede ver como una variable de orden superior a la estructura multidimensional, es decir, como una variable que representa una cualidad que no se puede medir pero que se manifiesta causalmente a través de dimensiones, las cuales sí se pueden medir con indicadores observables. Este tipo de conceptualización es empleada en los estudios sobre escalas GRS (ej. Sofologi et al., 2022). En segundo lugar, se puede interpretar como una variable latente que sí se puede medir a través de un indicador observable y0, y que influye causalmente al resto de variables latentes. En la Figura I la relación entre variables latentes sigue una expresión similar a (1), que para la primera dimensión es (2):
Donde γ10 representa el efecto de η0 sobre η1, y ζ1 es el error cometido en la determinación de η1.
La conceptualización habitual en esta área de conocimiento es la primera, tal y como se muestra, por ejemplo, en Pfeiffer et al. (2008), donde se plantea una concepción multidimensional de las altas capacidades con un factor subyacente “g” o factor de capacidad general1. Hay que reconocer que Tourón et al. (2023) son muy cautos y no afirman claramente este hecho, pero subrepticiamente parecen hacerlo cuando calculan una “media total de la escala”, como posteriormente explicaremos.
Por tanto, como hay un factor latente que no se puede medir directamente (no tenemos y0), se plantea la medición de dimensiones que son manifestaciones de ese factor. Y esta distinción es crucial, porque la estimación del valor verdadero2 de η0 entonces debe hacerse a través de esta especificación (3):
Así, se debe cumplir la igualdad (4):
Como el valor esperado de los errores e1, e2, e3,ζ1, ζ2, ζ3 se asume nulo (ruido blanco), y se ha debido fijar la escala de cada dimensión, que suponemos es un valor unitario (λ11=λ22=λ33=1) entonces (5):
Por tanto, para medir el verdadero valor3 del factor g conviene fijar su escala, lo que ahora significa que uno de los γ debe ser también fijado. Para ello tenemos que elegir una de las dimensiones como la “mejor” o la que mejor “mide” en este caso el factor g. Si, por ejemplo, hacemos γ10=1, entonces (6):
De este modo, con el indicador observable de la primera dimensión ya bastaría para estimar el verdadero valor del factor g4.
Recordemos que, según Edwards (2001), este tipo de constructos con dimensiones no existen separadamente de sus dimensiones, es decir, si se admite esta conceptualización, estaríamos diciendo que el factor g no existe sin concebir su propia multidimensionalidad. Una muestra de cómo testar este tipo de modelos (incluso de tercer orden, es decir, con dimensiones y factores de orden superior en dos niveles) se encuentra en Martínez y Martínez (2008). No obstante, este tipo de modelos son abiertamente criticados por Hayduk et al. (1995), como detallan Martínez y Martínez (2010a), admitiendo las limitaciones de su trabajo anterior de 2008.
Como bien es conocido, al realizar análisis factorial para testar el modelo se está interesado en la estructura de covarianza, no en las medias. Pero ello no es óbice para admitir que, si se especifican las relaciones causales del modelo (como el presentado en la Figura 1), la interpretación sobre el valor verdadero de cada variable latente es la que hemos explicado. De este modo, proponer un modelo multidimensional como se muestra en la parte izquierda de la Figura I, que refleja un factor g subyacente, implica desde el punto de vista de la medida, el factor g puede medirse con el “mejor” indicador de la “mejor” dimensión, es decir, con un único ítem. Y más aún, debe cumplirse (6), por lo que, con cualquier ítem de las otras dimensiones, se podría conocer el valor verdadero de g tan solo con la estimación del parámetro γ respectivo.
Esto es compatible, como no podría ser de otro modo, con la visión reflectiva sobre la medición, donde los ítems de una variable latente se pueden considerar intercambiables, lo que indica que quitando un ítem no se altera el significado de la variable latente. Variaciones en la variable latente se manifiestan en variaciones en los ítems que las miden. Del mismo modo, en un constructo multidimensional, variaciones en la dimensión subyacente se manifiestan en variaciones en sus múltiples dimensiones; quitando una dimensión no se altera el significado del constructo subyacente.
Parece obvio que esta interpretación no es la que los investigadores en altas capacidades desearían plantear, pero es la que admiten cuando emplean el modelo factorial. Llegados a este punto se necesita un enfoque diferente sobre la medición, cambiando la relación causal entre los indicadores y las variables latentes, hacia modelos formativos (Bollen y Lennox, 1991; Bollen y Diamantopoulus, 2017).
Los indicadores formativos no son intercambiables, y no tienen por qué correlacionar. Si se elimina uno de esos indicadores, se altera el significado de la variable latente, ya que esa variable se define a partir de esos indicadores. De este modo, la variable latente se define a partir de los indicadores observables (con matices explicados en Bollen y Diamantopolus, 2017), es decir, el significado de la variable latente depende de cómo se operacionalice su medición. Es una visión ciertamente constructivista, de gran utilidad práctica, que recoge perfectamente el objetivo de los modelos que plantean escalas cuyo valor total formado a partir de la agregación de ítems sirve para discriminar entre sujetos que poseen en mayor o en menor medida un determinado rasgo.
La discusión sobre los tipos de estructuras de medición formativas está fuera del objetivo de este trabajo, ya que es muy amplia su caracterización, y puede consultase en Bollen y Diamantopoulus (2017). Para el caso concreto de la escala GRS 2 analizada por Tourón et al. (2023), es quizá más adecuado remitir a propuestas como la de Hayduk et al. (2019), y que se ilustra en la parte denominada “modelo extendido” de la Figura I.
El indicador llamado f(y_w) es un indicador compuesto por los ítems de las diferentes dimensiones y1, y2, y3. y sus respectivos pesos w1, w2, w3, es decir, es una función de los indicadores observables (7):
Como es una combinación lineal determinista, no existe el término de error, por lo que, como indica la Figura I, ef = 0.
Esta conceptualización casa mucho más con el planteamiento de Tourón et al. (2023), quienes indican:
“El desarrollo de la dimensión de competencia socioemocional, se llevó a cabo con el objetivo de ampliar la evaluación de la alta capacidad, más allá de una lente tradicional que se enfoca principalmente en las “fortalezas de la cabeza” -que incluyen resolución de problemas, memoria, razonamiento y creatividad-, a una visión más holística y completa del estudiante que incluye las “fortalezas del corazón”, como las fortalezas personales e interpersonales (Pfeiffer, 2001, 2017b). Esencialmente, el propósito era incorporar una perspectiva de psicología positiva a la escala para padres GRS 2”.
Aquí son los investigadores los que definen qué es alta capacidad a partir de la instrumentalización de la medida. Es decir, y expresado de manera sencilla, se incluye una nueva dimensión porque creen que al hacerlo se define o evalúa mejor el concepto de alta capacidad. Por tanto, la evaluación de la alta capacidad dependerá de las dimensiones elegidas para su medición, y esta es una visión formativa de la medición, no reflectiva. De este modo, la caracterización de alta capacidad en un individuo dependerá de las puntuaciones en las diferentes dimensiones. Así, aquellos que obtengan puntuaciones altas en, por ejemplo, todas las dimensiones serán considerados como que tienen una mayor capacidad que aquellos que obtengan puntuaciones altas en una sola dimensión. En consecuencia, el valor de esa variable tan elusiva que se quiere medir como capacidad general depende de las puntuaciones en todas las dimensiones; se realiza un perfil de la capacidad de cada persona en función de su puntuación en cada dimensión y en la combinación de estas.
La última parte del modelo extendido de la Figura I la componen las variables latentes η4 y η5, que corresponden a efectos de la escala de medida y a una variable de control, respectivamente. Es decir, se expande el modelo factorial al considerar una estructura causal entre variables latentes, donde se tengan en cuenta los efectos de la escala de medida de altas capacidades y una (o varias, dado el caso) covariables exógenas que actúen como control de esos efectos. Este esquema, es similar al postulado por Hayduk et al. (2019), por lo que se puede emplear el enfoque descrito en ese trabajo para testar el modelo GRS 2.
Analogía con las altas capacidades físicas
El modelo presentado en la Figura I que representa un instrumento de medida de las altas capacidades intelectuales, es quizá más entendible si se postula su equivalente a la medición de las altas capacidades físicas.
Partamos de que η0 es una variable que representa la alta capacidad física que es un concepto elusivo y difícil de medir directamente. Entonces, se plantea una concepción multidimensional, en el que otras variables latentes entran en juego: por ejemplo, la velocidad, la fuerza y la resistencia aeróbica (Jung, 2022). Esas variables se miden a partir de indicadores observables (test de velocidad, test de fuerza, test de resistencia). Y esto es no es una conceptualización reflectiva, sino formativa, por las siguientes razones:
- Estamos definiendo la alta capacidad física a partir de esas 3 dimensiones que consideramos. Otro investigador podría desafiar este planteamiento y añadir otra dimensión, por ejemplo, la flexibilidad (ver Jung, 2022) con lo que la definición de alta capacidad física cambiaría.
- Las dimensiones consideradas no tienen por qué estar fuertemente asociadas, ya que aquellos que tengan más masa muscular y más fibras rápidas probablemente sean mejores en velocidad y fuerza, pero no tanto en resistencia.
- Las dimensiones no son intercambiables, y si se elimina una de ellas se altera el significado de la variable de interés (la alta capacidad física).
- La alta capacidad física no se puede medir a través de un indicador, como se desprende de la concepción reflectiva de la ecuación (6). Es decir, sería incorrecto estimar la alta capacidad física con solo la medición de una de las dimensiones, por lo que necesitamos todas las dimensiones sobre las que se ha definido el concepto de alta capacidad física para “medirlo”.
- Aquellos individuos que puntúen más alto en las 3 dimensiones serán considerados que tienen mayor capacidad física que los que puntúen alto en una dimensión, pero bajo en las otras dos.
De este modo, se podría construir una escala con una función de pesos a especificar por el investigador para formar el índice global f(yw). Y este índice se podría relacionar causalmente con variables de consecuencias η5, como, por ejemplo, el rendimiento del deportista en un equipo de fútbol, y añadir variables de control η4, como, por ejemplo, el sexo o la edad.
Estos argumentos, aunque simplistas, son didácticos, y nos hacen ver que la medición de las altas capacidades intelectuales debe seguir una modelización similar.
Test del modelo
Tourón et al. (2023) reportan la bondad de ajuste de su modelo original, y de las posteriores especificaciones que testan (comparan el ajuste de 8 modelos competitivos), no empleando el test de la chi-cuadrado como criterio5 (ajuste exacto) y, en su lugar, usando otra serie de índices de ajuste, entre ellos el RMSEA, TLI y otros: “Siguiendo a Hu y Bentler (1999), como evidencia de validez es suficiente un ajuste aceptable en la combinación de estos índices”.
Pocos años más tarde del estudio de Hu y Bentler (1999), diversos trabajos (Beauducel & Wittmann, 2005; Fan y Sivo, 2005; Marsh et al., 2004) cuestionaron el uso de criterios fijos, o “reglas de oro” para la evaluación de modelos con índices de ajuste “aproximado” (CFI, TLI, SRMR, RMSEA, etc.) como respuesta a las reglas de corte propuestas por Hu y Bentler (1999). Otros estudios posteriores también lo hicieron (ej. Niemand y Mai, 2018; McNeish y Wolf, 2023). Esos criterios comúnmente son usados para ajustar los modelos de forma que se evite el único test adecuado para detectar la mala especificación de un modelo (el test de la chi-cuadrado o, más correctamente, la familia de test de la chicuadrado) prueba que nos dice que, si el modelo es correcto, no será rechazada incluso con tamaños de muestra más grandes (ej. Hayduk y Glaser, 2000a,b; Barret, 2007; Hayduk et al., 2007; McIntosh, 2007; Antonakis et al., 2010; McIntosh 2012; Hayduk, 2014b; Ropovic, 2015; Rönkkö et al., 2016).
El grado de mal ajuste en la estructura de covarianza no está asociado al grado de mala especificación (Hayduk, 2014b), de este modo es incorrecto identificar la divergencia estadística sobre el modelo propuesto como un indicador de grado de idoneidad de este. En los modelos de ecuaciones estructurales se parte de una matriz de covarianzas entre los indicadores observables. Esa matriz se compara con la matriz de covarianzas implicadas por el modelo, la cual resulta de las restricciones de causalidad que estemos imponiendo. Esa matriz implicada por el modelo es la matriz poblacional, porque estipulamos que ése es el modelo que rige la población. Por tanto, el modelo especificado es la visión del mundo que queremos testar contra los datos, los cuales, salvo la propia variabilidad muestral (de ahí el test estadístico de la chi-cuadrado en función de sus grados de libertad), deben ajustarse exactamente.
El test de la chi-cuadrado puede fallar en ocasiones en detectar modelos mal especificados. Por ejemplo, es bien conocida la posible existencia de modelos equivalentes (mismo ajuste, pero con diferentes restricciones causales). De ahí que el compromiso teórico con el modelo sea tan importante para elegir entre modelos que se ajustan aquel que es congruente con la teoría que lo soporta. No obstante, y pese a esa limitación, sigue siendo la única vía posible de análisis, mejor que el resto de los índices que comúnmente se reportan, casi siempre citando el trabajo de Hu y Bentler (1999), como bien explica Hayduk (2014a).
De este modo, cuando un modelo no pasa el test de la chi-cuadrado, los parámetros estimados no son interpretables, ya que una o varias de las relaciones de covarianza implicadas por el modelo no es apoyada por los datos empíricos, lo que de inmediato produce sesgo en las estimaciones. Obviamente, no tiene sentido tampoco interpretar índices como la fiabilidad compuesta o la varianza media extraída. Si, por el contrario, el modelo se ajusta, entonces hay que considerar la posibilidad de modelos competitivos (teorías alternativas) y/o equivalentes que se puedan ajustar también, y elegir el que tenga un mejor ajuste en el caso de modelos en competencia (vía test de la diferencia de chi-cuadrado entre dos modelos competitivos que se ajustan) o el que sea teóricamente fundado en el caso de los modelos equivalentes (en línea con la concepción de causalidad que parte de aseveraciones cualitativas estipulada por Pearl, 2000).
Como se deriva de las anteriores líneas, este enfoque es mucho más exigente con los modelos que se plantean, sobre todo en ciencias sociales, donde existe una especie de “escritura automática” en investigación (Martínez y Martínez, 2009); se van reproduciendo errores e incorrecciones sistemáticamente, lo que hace que esos errores sean la postura mayoritaria, y esa postura, simplemente por ser mayoritaria, siga incitando a que otros la adopten. Hayduk (2014b) ilustra este hecho con una anécdota en el que uno de los creadores del software que fue, durante muchos, años el más empleado en esta metodología (LISREL) admitió que, como el test de la chi-cuadrado rechazaba muchos modelos, tuvieron que proponer otros indicadores de ajuste (GFI, AGFI, etc.) menos exigentes con los datos para que hubiera menos modelos rechazados, contentar a los investigadores y, de este modo, que el software tuviera más aceptación.
Análisis factorial
Tourón et al. (2023) emplean el análisis factorial exploratorio y confirmatorio: “Para probar la estructura de la escala se ha llevado a cabo un análisis factorial exploratorio y otro confirmatorio que aporten evidencias sobre la validez de la misma”.
Hayduk (2014b) demuestra que el análisis factorial exploratorio es incapaz de detectar la estructura real de los datos, es decir, de identificar el modelo que ha generado esos datos empíricos. Por tanto, no se puede probar un modelo teórico con un análisis exploratorio, simplemente tener una visión de la estructura correlacional de los datos.
Tourón et al. (2023) hacen un meritorio esfuerzo en dividir la muestra en dos partes. Sobre el primer 40% de la muestra emplean el análisis factorial exploratorio y sobre el 60% restante testan la estructura de 4 factores que encuentran en la fase exploratorio. Desde el punto de vista metodológico es loable esa filosofía de particionar los datos, aunque hubiera sido más correcto emplear las mismas particiones, pero de forma diferente. Así en la primera se podría haber puesto a prueba la estructura original de 3 factores mediante un análisis factorial confirmatorio, estudiando las posibles causas de desajuste (analizando, por ejemplo, los índices de modificación siempre que estén sustentados en la teoría). Si, tras analizar los índices de modificación, se hubiera recomendado una especificación diferente que se ajustara vía chi-cuadrado, entonces en el 60% restante de la muestra se podría haber testado esa nueva especificación con un nuevo análisis factorial confirmatorio.
Esta propuesta que acabamos de hacer dista, sin embargo, de ser la más óptima (aunque es mejor que realizar un análisis factorial exploratorio, ya que es más congruente con cualquier método hipotético-deductivo que pretenda probar la estructura de una escala). Aunque el test de la chi-cuadrado es más efectivo que la identificación de valores propios en el análisis factorial exploratorio (Hayduk, 2014b), también puede, en ocasiones, fallar al identificar el modelo correcto. Es entonces cuando, indefectiblemente, surge la necesidad de analizar la validez de constructo a través de la construcción de una red de causas y/o efectos de las variables latentes sobre las que se esté estudiando su validez, es decir, postular una red nomológica, tal y como Cronbach y Meel (1955) también defendían.
Como vuelve a recordar Hayduk (2014b) poniendo a prueba el constructo en esa red nomológica se interroga la capacidad del factor latente de producir sus indicadores observables, y eso es indispensable para hablar de validez de constructo (Cronbach y Meehl, 1955). De este modo, en todo estudio en el que se pretenda validar un instrumento de medida, debe aparecer un “modelo extendido” según la terminología que hemos empleado en la Figura I, es decir, ir más allá del análisis factorial e incluir el constructo o los constructos de interés en una red nomológica. Es entonces cuando los modelos de ecuaciones estructurales llegan a su máximo potencial, pudiendo poner a prueba ese modelo contra los datos empíricos, es decir, la matriz de covarianzas implicada por las restricciones causales del modelo contra la matriz de covarianza de los indicadores observables.
Existen numerosas críticas a una forma de proceder en psicometría que, no por extendida, es correcta. Se trata de tratar de validar un instrumento de medida con análisis factorial exploratorio (aunque luego se haga un análisis factorial confirmatorio), o con un análisis factorial confirmatorio (aunque luego se teste el modelo causal, lo que es conocido como “análisis en dos pasos”). La razón fundamental de esas críticas es la relativa al concepto de validez de constructo, explicado en Cronbach y Meel (1955); la medición no se puede separar de la teoría, y la validez de constructo necesita de una red nomológica para poder ser analizada. Ejemplos de esas críticas se pueden encontrar en Fornell y Yi (1992), Hayduk y Glasser (2000a) o Hayduk (2014b).
Número de ítems por variable latente
Tourón et al. (2023) tradujeron los 20 ítems originales de la escala GRS 2 para padres, agrupados en las 3 dimensiones mencionadas (6, 7, y 7, respectivamente). Como Tourón et al. (2023) no indican la redacción de los ítems es muy complejo valorar la idoneidad de los mismos para reflejar la dimensión subyacente. No obstante, y a estas alturas de este manuscrito, ya sabemos que en un modelo reflectivo el valor verdadero de cada dimensión latente se puede estimar a partir del valor de cada indicador observable (1). Los indicadores observables son reflectivos según la especificación de Tourón et al. (2023) por lo que con solo un indicador se podría medir cada una de esas dimensiones. Si un investigador piensa que con un solo indicador es insuficiente para medir una variable latente y que necesita más porque la dimensión latente es amplia (como indican Tourón et al. (2023)), lo que probablemente está sucediendo es que esa batería de indicadores está midiendo variables latentes diferentes, es decir, no son la manifestación de una única variable latente, sino de varias.
El usar un solo indicador por variable latente en la Figura I no es solo un modo de simplificar el esquema, sino que es una forma de reflejar las investigaciones que defienden las medidas de un solo ítem por variable latente cuando, evidentemente, la variable latente se manifiesta a través de observables reflectivos (ej. Bergkvist y Rossiter, 2007; Matthews et al., 2022; Allen y Pistone, 2023; Wulf et al., 2023). Como indican Durvasula et al. (2012), hay literatura que sugiere que las escalas largas amenazan a la validez de constructo, y producen fatiga en la persona que responde. Además, cuando se emplea el mismo formato de escala Likert, es decir, el mismo rango a una numerosa batería de ítems, existe riesgo serio de sesgo de método común (Jordan y Troth, 2020), y una de sus manifestaciones puede ser precisamente lo que Tourón et al. (2023) parecen considerar como algo positivo cuando aluden a las correlaciones altas entre cada ítem y el resto señalando la “homogeniedad del conjunto de ítems”. Es más, hay ejemplos en la propia literatura sobre altas capacidades y escalas GRS donde se vislumbra un efecto halo que afecta obviamente a la validez (ej. Jabůrek et al., 2020).
Una explicación exhaustiva de la necesidad de emplear un solo ítem (el mejor indicador posible), o en determinados casos, un segundo ítem que acompañen a ese mejor indicador puede encontrarse en Hayduk (1996) o en Hayduk y Littvay (2012). En el contexto de ecuaciones estructurales, Hayduk (1996) propone además fijar la varianza de error de ese mejor indicador, haciendo que el investigador se comprometa con el significado de la variable latente, evitando de esta forma el denominado interpretational confounding, es decir, el cambio entre la relación entre la variable latente y su mejor indicador cada vez que cambia la estructura de covarianza de los datos al añadir otras variables en el modelo.
De este modo, en la Figura I sería necesario no solo fijar todos los λ (que hemos dicho que era primordial para escalar cada variable latente), sino también las varianzas de error de cada indicador, usualmente a un porcentaje muy reducido de lo que sería la varianza del ítem observable. El modelo representado en la Figura I se podría ampliar a dos ítems por variable latente. De hecho, esto añadiría robustez a la conceptualización porque ese segundo ítem (el segundo mejor indicador posible) no tendría fijada ni la carga factorial ni la varianza de error, por lo que las nuevas covarianzas añadidas a la matriz de covarianzas muestral producirían un test más sólido de las restricciones producidas por la fijación de la carga factorial y de la varianza de error de esos mejores indicadores.
Como explican Hayduk y Littvay (2012) si los indicadores son reflectivos no es conveniente utilizar tantos ítems por variable latente, porque lo que se hace es saturar la parte latente del modelo con correlaciones factoriales. Si se necesitan un gran número de ítems por variable latente porque desde el punto de vista teórico el dominio de la variable es amplio, insistimos en que lo más probable es que, o se estén midiendo en realidad varias variables latentes, o se esté vislumbrando una estructura formativa en lugar de reflectiva.
Modelos alternativos
Existen otras especificaciones de modelos compatibles con toda la argumentación anterior, y que son diferentes a la Figura I, tal y como se muestran en la Figura II, III y IV.
FIGURA II. Modelo alternativo sin escala global
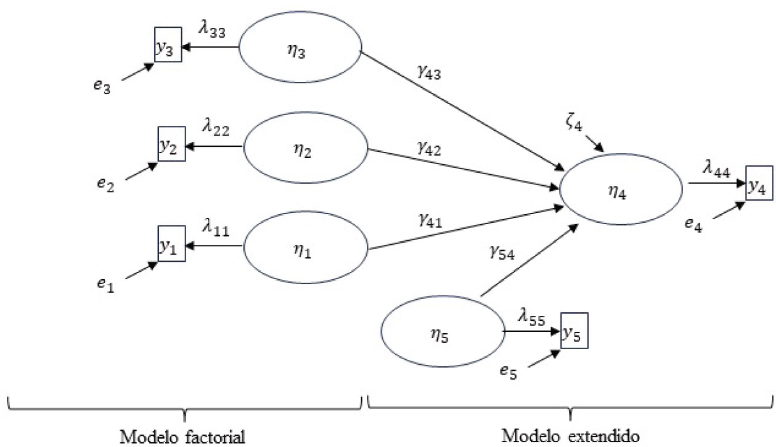
FIGURA III. Modelo alternativo sin escala global y con causas de dimensiones
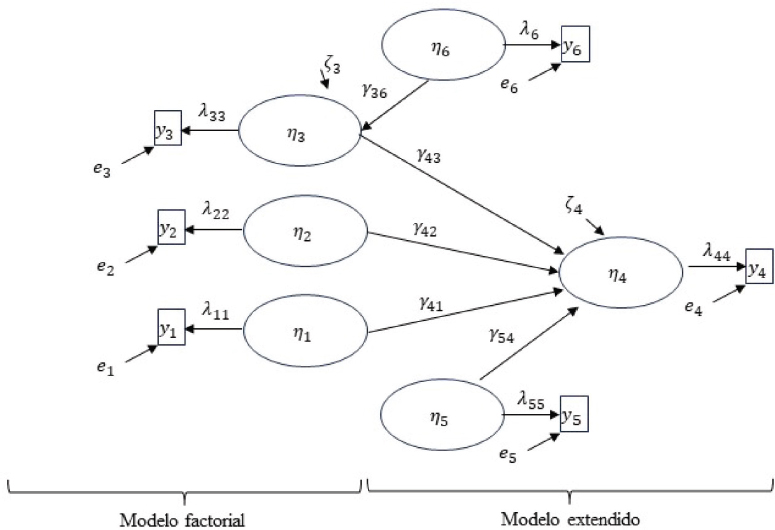
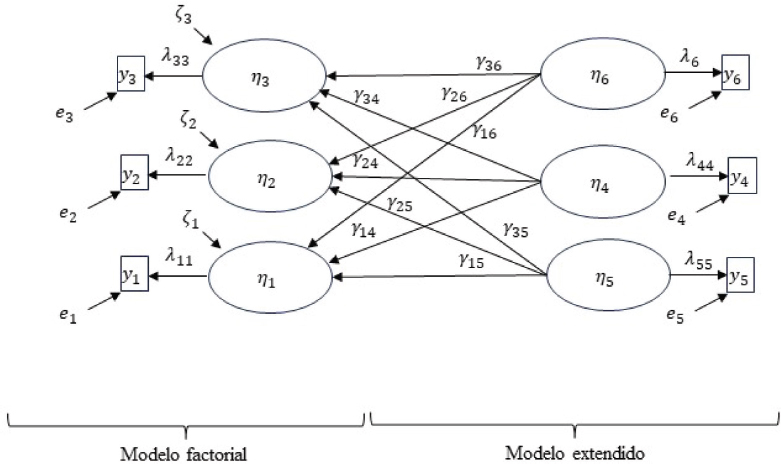
FIGURA IV. Modelo alternativo con causas de las dimensiones de altas capacidades
En la Figura II se representa un modelo similar al de la Figura I, salvo que ahora no se pretende construir ningún índice global que mida la capacidad como función de las dimensiones, sino que la teoría es más prudente y admite que existen dimensiones η1, η2, η3 que se pueden medir de forma reflectiva con y1, y2, y3, asociadas a las altas capacidades, aunque no se especifica cuál es ese tipo de relación funcional (de ahí que es una especificación más conservadora). Esas dimensiones influyen en una variable consecuencial η5 (por ejemplo, alguna variable de rendimiento, como especifican Kelly y Peverly, 1992) de la que se puede medir su efecto a través de los coeficientes γ, y en la que hay una variable de control η4 (o varias, aunque por simplicidad solo se ha propuesta una) que podría ser, por ejemplo, alguna variable socioeconómica o demográfica.
En la Figura III se amplía aún más el modelo propuesto en la Figura II, siendo todavía más interesante desde el punto de vista causal porque incluye una variable η6 que puede provocar variación en una de las dimensiones, como por ejemplo el contexto familiar sobre la creatividad (Manzano y Arranz, 2008).
En la Figura IV no se muestran consecuencias de las dimensiones de altas capacidades, sino posibles causas. Este esquema es (con matices) equivalente al utilizado por Pfeiffer et al. (2008) para validar la escala GRS-S, proponiendo variables que pueden causar variación en las dimensiones que ellos emplean (6 en lugar de las 3 de la Figura IV), donde como esas variables latentes exógenas η4, η5, η6, emplean el género, la raza y la edad. Evidentemente lo hacen usando otra metodología estadística (análisis multigrupo de la varianza), pero el diagrama causal es equivalente al mostrado en la Figura IV. Para testar la hipótesis que Pfeiffer et al. (2008) estipulan de que la escala GRS-S no debería discriminar entre género, raza y edad, en un modelo de ecuaciones estructurales simplemente habría que fijar todos los parámetros γ a cero, y poner a prueba esas restricciones de causalidad con el test de la chi-cuadrado. Recordemos que los modelos de ecuaciones estructurales permiten emplear variables exógenes dicotómicas, y que cualquier variable es susceptible de ser considerada latente debido al error de medición. Por ejemplo, el sexo o la edad pueden tener errores de codificación, por lo que se puede fijar la varianza de error de sus indicadores no necesariamente a cero.
Hay que matizar que Pfeiffer et al. (2008) no emplean un ítem para medir cada dimensión, sino varios (12 por cada una de las 6 dimensiones), con lo que las críticas realizadas en este manuscrito con relación a la confusión entre indicadores reflectivos y formativos, y lo que ello implica para la modelización estarían vigentes.
Por tanto, cualquiera de las propuestas de modelización expresadas en las Figuras II, III y IV, hubieran ayudado a Tourón et al (2023) a analizar más rigurosamente la validez de constructo de su adaptación de la escala GRS 2 al entorno español.
Discusión
El estudio de Tourón et al. (2023), aunque realiza un esfuerzo procedimental meritorio para analizar la validez de constructo de la escala GRS 2 para padres en el ámbito español, adolece de elementos esenciales que cuestionan su validez.
El primero de ellos se refiere a la especificación de un modelo reflectivo en lugar de formativo. Tourón et al. (2023) consideran tanto los ítems de cada dimensión como las propias dimensiones de carácter reflectivo (Edwards, 2001). Así los especifican en la relación causal entre las variables latentes y sus respectivos ítems, y en la relación entre los factores de segundo orden y las dimensiones. Aunque los autores no muestran en su artículo la batería de ítems completa, sí que comentan alguno de ellos, como los ítems 5, 8 y 15 que los autores sitúan como manifestación de la dimensión (al final identificada como subdimensión) “control emocional”. Esos ítems se refieren al control del estrés, la ira y la perseverancia en el trabajo, lo que precisamente sugiere que son indicadores de variables latentes diferentes o que deberían ser causa y no efecto de esa variable etiquetada (construida y definida en base a sus indicadores) “control emocional”. El construir escalas sumativas con los ítems de cada dimensión o en una única escala global para dar un perfil de capacidad de cada individuo es una visión formativa, cuya perspectiva de análisis se muestra en la Figura I, requiriendo, por tanto, añadir a la estructura factorial otras variables que se relacionen con la escala o escalas construidas. Esta visión formativa estaría en consonancia con la visión de Boring (1923) sobre la inteligencia y los test para medirla6.
El segundo aspecto problemático del estudio de Tourón et al. (2023) es la no admisión de que todos los modelos testados (ocho en total) son incompatibles con los datos empíricos y, por tanto, los modelos son incorrectos, es decir, no válidos. Es cierto que en la literatura especializada de ecuaciones estructurales hay investigadores (ej. Jöreskog, 1978; Bentler, 1990; Steiger; 2007; Browne et al., 2002) que critican la prueba chi-cuadrado y recomiendan los índices de ajuste aproximados. Curiosamente Jöreskog, Bentler, Steiger y Browne fueron creadores de software comercial de ecuaciones estructurales (LISREL, EQS, SEPATH, y RAMONA respectivamente). Otros investigadores siguen en esa misma línea (ej. McNeish y Wolf, 2023). Sin embargo, las principales críticas al test de ajuste exacto son respondidas una a una por Hayduk (2014b). Una de las más recurrentes críticas es el mantra de que “todos los modelos son falsos”, por lo que no tendría sentido buscar el ajuste exacto. Aunque Hayduk (2014b) responde también a esa crítica, conviene consultar fuera del ámbito de las ecuaciones estructurales, y en un campo más general sobre teoría de probabilidad y modelización de datos e inferencia estadística (ej. Spanos, 2019). Precisamente Spanos (2021) recuerda que existe una mala interpretación de ese “mantra” ya que hay que saber distinguir entre un modelo sustantivo (basado en una teoría) y el modelo estadístico implícito en él, en el cual se encuadran un conjunto de asunciones probabilísticas impuestas sobre los datos. Así, los investigadores que aluden a que “todos los modelos son falsos” intentan justificar que la mala especificación estadística es inevitable y, por tanto, no tiene sentido buscar el ajuste exacto. Pero eso es erróneo, porque ese lema se refiere a los modelos sustantivos que, obviamente, son una representación más simplificada de la realidad. Sin embargo, lo que se testa vía chi-cuadrado en los modelos de ecuaciones estructurales no es si el modelo sustantivo es “verdad”, sino si el modelo estadístico implícito es congruente con los datos empíricos, el cual está compuesto inseparablemente de las restricciones causales y de las asunciones probabilísticas. De ahí la importancia de la teoría en construir un modelo causal, y de ahí que haya que ser rigurosos en respetar la evidencia marcada por la discrepancia entre el modelo propuesto y los datos empíricos cuando las asunciones del modelo se cumplen, tal y como Spanos (2019) explica de forma general en la modelización de datos.
Esto nos lleva indefectiblemente al tercer elemento de crítica a Tourón et al. (2023) relacionado con el uso de análisis factorial para el estudio de la validez de constructo, y la necesidad de estipular una red nomológica que pueda ser testada globalmente. Bien es cierto que, como se indica en Lissitz (2009), existen también propuestas sobre el abandono de los procesos de validación recomendados por Cronbach y Meehl (1955) y enfocarse en una perspectiva ontológica, como la defendida en Borsbom et al. (2004): un test es válido para medir un atributo si y sólo si (a) el atributo existe y (b) variaciones en el atributo causalmente producen variaciones en los resultados del procedimiento de medición. Sin embargo, las tesis de Hayduk (1996) y Borsrbom et al. (2004) comparten más de lo que disienten, como analizan Martínez y Martínez (2009), por lo que no debe haber disconformidades sustanciales con los argumentos expuestos en este trabajo.
El número de ítems por variable latente es la cuarta crítica a Tourón et al. (2023). Aunque, como se ha indicado anteriormente, es más que probable que varios de los ítems del instrumento GRS 2 sean formativos, si se estipulan como reflectivos no hay necesidad de saturar el instrumento con tantos ítems que puedan provocar diferentes tipos de sesgo. Sin embargo, si los investigadores defienden la necesidad de todos esos ítems por la amplitud de los conceptos medidos y porque son necesarios para recoger las características de lo que se quiere medir entonces implícitamente se estaría admitiendo una estructura formativa, no reflectiva.
Hemos propuesto, además, modelos diversos que siguen la misma filosofía que muestra la Figura I, y que se cubrirían las limitaciones de la propuesta de Tourón et al. (2023). No son únicos, ya que existen otras propuestas en investigación en altas capacidades que ya se aventuran por especificaciones cercanas, como Nakano et al. (2016) y su modelo MIMIC (múltiples causas y múltiples indicadores). Es más, como también hemos indicado Pfeiffer et al. (2008) emplea una forma similar (aunque no tan rigurosa estadísticamente) de análisis de validación de la escala GRS-S como la especificada en la Figura IV.
En esos modelos de las Figuras II, III y IV no se plantea explícitamente que haya un factor de orden superior de capacidad que se manifieste a través de dimensiones. Una futura línea de investigación atrayente sería realizar un enfoque similar al de redes en psicopatología (Borsboom y Cramer, 2013; Fonseca-Pedrero, 2017), considerando esas dimensiones de capacidad como “síntomas” que se relacionan complejamente en una red de interacción. Ninguna de las concepciones que hemos propuesto es incompatible con esa visión, ya que se dejan libres las correlaciones entre esas dimensiones de capacidad.
Los ejemplos de modelización mostrados en las Figuras I a IV son solo una referencia. Obviamente deben adaptarse al conjunto de variables latentes de cada contexto. Sin embargo, conviene aclarar que se necesita especificar muy bien qué se está midiendo y qué variable se consideran como un tipo de dotación o no. Tourón et al. (2023) indican que las habilidades socioemocionales no se ven como un tipo de dotación, por tanto, a la hora de explicar qué significa multidimensionalidad en altas capacidades y especificarlo en un modelo hay que tener clara esa distinción.
Otras críticas al instrumento de medida GRS 2 también serían importantes de debatir, aunque ya superarían la extensión de este trabajo. Entre ellas, por ejemplo, estaría la discusión sobre el uso de escalas tipo Likert ordinales con etiquetas lingüísticas, dado que puede haber interacción entre esas etiquetas lingüísticas y la numeración de la escala Likert. A este respecto, enfoques basados en lógica borrosa podrían ayudar a dilucidar la idoneidad de esas escalas (ver Martínez y Martínez, 2010; Martínez et al., 2010). En cualquier caso, reportar valores medios, como hacen Tourón et al (2023) en escalas ordinales es, cuanto menos, cuestionable (Liddell y Kruschke, 2018).
Finalmente, y dado que Tourón et al. (2023) admiten que su estudio es una validación preliminar y que se debe corroborar con investigaciones posteriores, sugerimos que se consideren los postulados argumentados en este manuscrito para seguir avanzando en la medición de las altas capacidades.
Referencias bibliográficas
Allen, B., & Pistone, L. F. (2023). Psychometric evaluation of a single-item screening tool for the presence of problematic sexual behavior among preteen children. Child abuse & neglect, 143, 106327. https://doi.org/10.1016/j.chiabu.2023.106327
Antonakis, J., Bendahan, S., Jacquart, P., Lalive, R. (2010). On making causal claims: A review and recommendations. Leadership Quarterly, 21, 1086-1120. https://doi.org/10.1016/j.leaqua.2010.10.010
Barret P. (2007). Structural equation modelling: Adjudging model fit. Personality and Individual Differences, 42(5), 815-824. https://doi.org/10.1016/j.paid.2006.09.018
Beauducel, A., & Wittmann, W. W. (2005). Simulation Study on Fit Indexes in CFA Based on Data With Slightly Distorted Simple Structure. Structural Equation Modeling, 12(1), 41–75. https://doi.org/10.1207/s15328007sem1201_3
Bentler, P. M. (1990). Comparative fit indexes in structural models. Psychological Bulletin, 107(2), 238–246. https://doi.org/10.1037/0033-2909.107.2.238
Bergkvist, L. , & Rossiter, J. R. (2007). The predictive validity of multiple-item versus single-item measures of the same constructs. Journal of Marketing Research, 44 (2), 175-184 https://doi.org/10.1509/jmkr.44.2.175
Bollen, K., & Lennox, R. (1991). Conventional wisdom on measurement: A structural equation perspective. Psychological Bulletin, 110(2), 305–314. https://doi.org/10.1037/0033-2909.110.2.305
Bollen K. A. (2002). Latent variables in psychology and the social sciences. Annual review of psychology, 53, 605–634. https://doi.org/10.1146/annurev.psych.53.100901.135239
Bollen, K. A., & Diamantopoulos, A. (2017). In defense of causal-formative indicators: A minority report. Psychological Methods, 22(3), 581–596. https://doi.org/10.1037/met0000056
Boring, E. G. (1923). Intelligence as the test measures it. The New Republic, 35, 35-37.
Borsboom, D., & Cramer, A. O. (2013). Network analysis: an integrative approach to the structure of psychopathology. Annual Review of Clinical Psychology, 9, 91–121.
Borsboom, D., Mellenbergh, G. J., van Heerden, J. (2004). The concept of validity. Psychological Review, 111(4), 1061-1071.
Browne, M. W., MacCallum, R. C., Kim, C. T., Andersen, B. L., Glaser, R. (2002). When fit indices and residuals are incompatible. Psychological Methods, 7(4), 403–421. https://doi.org/10.1037//1082-989x.7.4.403
Cronbach, L. J., & Meehl, P. E. (1955). Construct validity in psychological test. Pyschological Bulletin, 52, 218-302. https://doi.org/10.1037/h0040957
Durvasula, S., Sharma, S., Carter, K. (2012). Correcting the t statistic for measurement error. Marketing Letters, 23(3), 671–682. https://doi.org/10.1007/s11002-012-9170-9
Edwards, J. R. (2001). Multidimensional constructs in organizational behavior research: Towards an integrative and analytical framework. Organizational Research Methods, 4, 144–192.
Fan, X., & Sivo, S. A. (2005). Sensitivity of fit indexes to misspecified structural or measurement model components: Rationale of two-index strategy revisited. Structural Equation Modeling, 12, 334-367. https://doi.org/10.1207/s15328007sem12031
Fonseca-Pedrero, E. (2017). Análisis de redes: ¿una nueva forma de comprender la psicopatología? Revista de Psiquiatría y Salud Mental, 10(4), 206-215.
Fornell, C. & Yi, Y. (1992). Assumptions of the Two-Step Approach to Latent Variable Modeling. Sociological Methods & Research, 20, 291-320.
Hayduk, L. A. (1996). LISREL Issues, Debates and Strategies. Baltimore, MD: Johns Hopkins University Press.
Hayduk, L. A. (2014a). Seeing perfectly-fitting factor models that are causally misspecified: Understanding that close-fitting models can be worse. Educational and Psychological Measurement, 74(6), 905-926. https://doi.org/10.1177/0013164414527449
Hayduk, L. A. (2014b). Shame for disrespecting evidence: The personal consequences of insufficient respect for structural equation model testing. BMC: Medical Research Methodology, 14, 124 https://doi.org/10.1186/1471-2288-14-124
Hayduk, L. A., Cummings, G. Boadu, K., Pazderka-Robinson, H., & Boulianne, S. (2007). Testing! testing! one, two, three – Testing the theory in structural equation models! Personality and Individual Differences, 42(5), 841-850.
Hayduk, L. A., Estabrooks, C. A., Hoben, M. (2019). Fusion Validity: Theory-Based Scale Assessment via Causal Structural Equation Modeling. Frontiers in Psychology, 10, 1139. https://doi.org/10.3389/fpsyg.2019.01139
Hayduk, L. A., & Glaser, D. N. (2000a). Jiving the four-step, waltzing around factor analysis, and other serious fun. Structural Equation Modeling, 7(1), 1-35.
Hayduk, L. A., & Glaser, D. N. (2000b). Doing the four-step, right-2-3, wrong-2-3: A brief reply to Mulaik and Millsap; Bollen; Bentler; and Herting and Costner. Structural Equation Modeling, 7(1), 111-123.
Hayduk, L. A., & Littvay, L. (2012). Should researchers use single indicators, best indicators, or multiple indicators in structural equation models? BMC Medical Research Methodology, 12, 159, 1-17. https://doi.org/10.1186/1471-2288-12-159
Hayduk, L.A., Ratner, P.A., Johnson, J.L., Bottorff, J.L. (1995). Attitudes, ideology and the factor model. Political Psychology, 16, 479–507.
Hu, L. T., & Bentler, P. M. (1999). Cutoff Criteria for Fit Indexes in Covariance Structure Analysis: Conventional Criteria versus New Alternatives. Structural Equation Modeling, 6(1), 1–55. https://doi.org/10.1080/10705519909540118
Jabůrek, M., Ťápal, A., Portešová, Š., Pfeiffer, S. I. (2020). Validity and Reliability of Gifted Rating Scales-School Form in Sample of Teachers and Parents – A Czech Contribution. Journal of Psychoeducational Assessment, 39(3), 361–371. https://doi.org/10.1177/0734282920970718
Jordan, P. J., & Troth, A. C. (2020). Common method bias in applied settings: The dilemma of researching in organizations. Australian Journal of Management, 45(1), 3-14. https://doi.org/10.1177/0312896219871976
Jöreskog, K. G. (1978). Structural analysis of covariance and correlation matrices. Psychometrika, 43, 443-477.
Jung J. Y. (2022). Physical giftedness/talent: A systematic review of the literature on identification and development. Frontiers in Psychology, 13, 961624. https://doi.org/10.3389/fpsyg.2022.961624
Kelly, M. S. & Peverly, S. T. (1992). Identifying bright kindergartners at risk for learning difficulties: Predictive validity of a kindergarten screening tool. Journal of School Psychology, 30, 245-258.
Liddell, T. M. & Kruschke, J. K. (2018). Analyzing ordinal data with metric models: What could possibly go wrong? Journal of Experimental Social Psychology, 79, 328-348. https://doi.org/10.1016/j.jesp.2018.08.009
Lissitz, R. W. (Editor) (2009). The Concept of Validity: Revisions, New Directions, and Applications. Charlotte, NC: Information Age Publishing.
MacCallum, R. C., & Austin, J. T. (2000). Applications of Structural Equation Modeling in Psychological Research. Annual Review of Psychology, 51, 201-226. https://doi.org/10.1146/annurev.psych.51.1.201
Manzano, A. Arranz, F., Enrique B. (2008). Contexto familiar, superdotación, talento y altas capacidades». Anuario de psicología / The UB Journal of psychology, 39(3), 289-309, https://raco.cat/index.php/AnuarioPsicologia/article/view/123643
Marsh, H. W., Hau, K. T., Wen, Z. (2004). In search of golden rules: Comment of hypothesis-testing approaches to setting cutoff values for fit indexes and dangers in overgeneralizing Hu and Bentler's (1999) findings. Structural Equation Modeling, 11, 320-341. https://doi.org/10.1207/s15328007sem11032
Martínez, J. A., Ko, Y. J., & Martínez, L. (2010). An application of fuzzy logic to service quality research: A case of fitness service. Journal of Sport Management, 24, 502-523. https://doi.org/10.1123/jsm.24.5.502
Martínez, J. A. & Martínez, L. (2009). El análisis factorial confirmatorio y la validez de escalas en modelos causales. Anales de Psicología, 25(2), 368-374.
Martínez, J. A. & Martínez, L. (2010). Re-thinking perceived service quality. An alternative to hierarchical and multidimensional models. Total Quality Management & Business Excellence, 21(1), 93-118
Martínez, J. A. & Martínez, L. (2010). La medición de la satisfacción de servicios deportivos a través de la lógica borrosa. Revista de Psicología del Deporte, 19(1), 41-58.
Martínez, L., & Martínez, J. A. (2008). Developing a multidimensional and hierarchical service quality model for the travel agencies industry. Tourism Management, 29, 706–720.
Matthews, R. A., Pineault, L. & Hong, Y. H. (2022). Normalizing the use of single-item measures: Validation of the single item compendium for organizational psychology. Journal of Business and Psychology, 37, 639-673. https://doi.org/10.1007/s10869-022-09813-3
McIntosh, C. N. (2007). Rethinking fit assessment in structural equation modelling: A commentary and elaboration on Barrett (2007). Personality and Individual Differences, 42(5), 859–867. https://doi.org/10.1016/j.paid.2006.09.020
McIntosh, C. N. (2012). Improving the evaluation of model fit in confirmatory factor analysis: A commentary on Gundy, CM, Fayers, PM, Groenvold, M., Petersen, M. Aa., Scott, NW, Sprangers, MAJ, Velikov, G., Aaronson, NK (2011). Comparing higher-order models for the EORTC QLQ-C30. Quality of Life Research. Quality of Life Research, 21(9), 1619-1621.
McNeish, D., & Wolf, M. G. (2023). Dynamic fit index cutoffs for confirmatory factor analysis models. Psychological Methods, 28(1), 61–88. https://doi.org/10.1037/met0000425
Nakano, T. D., Primi, R., Ribeiro, W. D., Almeida, L. D. (2016). Multidimensional Assessment of Giftedness: criterion Validity of Battery of Intelligence and Creativity Measures in Predicting Arts and Academic Talents. Anales De Psicologia, 32, 628-637.
Niemand, T. & Mai, R. (2018). Flexible Cutoff Values for Fit Indices in the Evaluation of Structural Equation Models. Journal of the Academy of Marketing Science, 46(6), 1148-1172.
Pearl, J. (2000). Causality: Models, reasoning, and inference. Cambridge University Press.
Pfeiffer, S. I., Petscher, Y., & Kumtepe, A. (2008). The Gifted Rating Scales-School Form: A Validation Study Based on Age, Gender, and Race. Roeper review, 30(2), 140–146. https://doi.org/10.1080/02783190801955418
Rönkkö, M., McIntosh, C. N., Antonakis, J., Edwards, J. R. (2016). Partial least squares path modeling: Time for some serious second thoughts. Journal of Operations Management, 47–48, 9–27. https://doi.org/10.1016/j.jom.2016.05.002
Ropovik, I. (2015). A cautionary note on testing latent variable models. Frontiers in Psychology, 6. https://doi.org/10.3389/fpsyg.2015.01715
Sofologi, M., Papantoniou, G., Avgita, T., Lyraki, A., Thomaidou, C., Zaragas, H., Ntritsos, G., Varsamis, P., Staikopoulos, K., Kougioumtzis, G., Papantoniou, A., & Moraitou, D. (2022). The Gifted Rating Scales-Preschool/Kindergarten Form (GRS-P): A Preliminary Examination of Their Psychometric Properties in Two Greek Samples. Diagnostics (Basel, Switzerland), 12(11), 2809. https://doi.org/10.3390/diagnostics12112809
Spanos. A. (2019). Probability Theory and Statistical Inference: Empirical Modeling with Observational Data, Cambridge University Press, Cambridge
Spanos, A. (2021). Modeling vs. inference in frequentist statistics: ensuring the tustworthiness of empirical evidence. Descargado desde: https://errorstatistics.files.wordpress.com/2021/03/modeling-vs-inference-3-2021.pdf
Steiger, J. H. (2007). Understanding the limitations of global fit assessment in structural equation modelling. Personality and Individual Differences, 42(5), 893-898.
Tourón, M., Navarro-Asensio, E., Tourón, J. (2023). Validez de Constructo de la Escala de Detección de alumnos con Altas Capacidades para Padres, (GRS 2), en España. Revista de Educación, 1(402), 55-83. https://doi.org/10.4438/1988-592X-RE-2023-402-595
Wulf, J. N., Sajons, G. B., Pogrebna, G. et al. (2023). Common methodological mistakes. The Leadership Quarterly, 34(1), 101677, https://doi.org/10.1016/j.leaqua.2023.101677
Información de contacto: José A. Martínez García, Universidad Politécnica de Cartagena. Facultad de Ciencias de la Empresa. Departamento de Economía de la Empresa. Calle Real, 3, 3021, Cartagena. E-mail: josean.martinez@upct.es
_______________________________
1 No es objetivo de este trabajo discutir acerca de las diferentes conceptualizaciones de las altas capacidades. Es evidente que la literatura es muy amplia al respecto y que hay discusión acerca de la definición, las políticas y las prácticas, como bien muestran Mcclain y Pfeiffer (2012). Simplemente vamos a considerar que se conciben las altas capacidades como una variable multidimensional o como una variable que no se puede medir directamente y que se manifiesta a través de diferentes dimensiones o rasgos.
2 Es evidente que si los datos se parametrizan como desviaciones con respecto a la media el valor “verdadero” medio de cada variable latente es cero.
3 Insistimos en que no estamos necesariamente admitiendo que se pueda medir un “verdadero valor” del factor g, sino simplemente estamos empleando la misma jerga que se emplea en el uso de variables latentes en este tipo de modelización. Lo importante es lo que representan las ecuaciones relacionando las variables del modelo, más allá de que un valor numérico concreto tenga sentido o no, cuando es evidente que las escalas de medida son arbitrarias. Así, lo que se cuestiona es el modelo a través del análisis de las ecuaciones que lo representan.
4 Si no se fijara la escala la interpretación sería idéntica, esta vez simplemente que el verdadero valor de g estaría ponderado por un coeficiente causal entre g y la dimensión pertinente, pero seguiría bastando con un único observable por cada dimensión para calcular ese valor de g.
5 Recordemos que el valor de la chi-cuadrado dividido por los grados de libertad, que sí reportan los autores, no es ningún test estadístico.
6 De nuevo no pretendemos entablar una discusión más profunda sobre los conceptos de inteligencia, capacidad, etc. Solo argumentamos que una visión formativa nos diría que lo que estamos midiendo viene determinado por cómo lo hemos definido previamente. Por tanto, la clave está en cómo se defina el concepto que se quiere medir.