Figura 1. Número de visualizaciones de los applets analizados
ÁLVARO BARRERAS (1), LUIS DUBARBIE (1) Y ANTONIO M. OLLER-MARCÉN (2)
(1) Universidad Internacional de La Rioja (España)
(2) Centro Universitario de la Defensa de Zaragoza (España)
DOI: 10.13042/Bordon.2022.93361
Fecha de recepción: 07/02/2022 • Fecha de aceptación: 21/07/2022
Autor de contacto / Corresponding author: Álvaro Barreras. E-mail: alvaro.barreras@unir.net
Cómo citar este artículo: Barreras, Á., Dubarbie, L. y Oller-Marcén, A. M. (2022). Análisis de applets de GeoGebra para la enseñanza del límite de una función. Bordón, Revista de Pedagogía, 74(4), 65-83. https://doi.org/10.13042/Bordon.2022.93361
INTRODUCCIÓN. La importancia de GeoGebra como una de las principales herramientas que ofrecen a los docentes de matemáticas la posibilidad de trabajar con simulaciones virtuales en sus aulas es indiscutible. Sin embargo, los recursos del repositorio oficial de GeoGebra no pasan ningún proceso de revisión. Por lo tanto, el criterio del docente a la hora de seleccionar este tipo de recursos es clave y se hacen necesarias herramientas que permitan analizar applets de GeoGebra para su implementación. En particular, este tipo de recursos ofrecen numerosas ventajas para la enseñanza del concepto matemático de límite de una función, frente a otro tipo de herramientas. MÉTODO. En este trabajo se analiza la idoneidad didáctica de applets de GeoGebra para la enseñanza del límite de una función. Se ha realizado un estudio exploratorio y descriptivo. El análisis se ha llevado a cabo mediante un enfoque deductivo con base en cinco variables diferentes (tipo de límite, interactividad, imagen conceptual, representación y acción). La muestra analizada, elegida mediante un muestreo de tipo intencional, es de 150 applets del repositorio de materiales de GeoGebra. RESULTADOS. Se muestran los resultados tras analizar las cinco variables establecidas para cada uno de los applets estudiados. También se analiza la influencia de la interactividad con el resto de las variables, así como la influencia de la cantidad de representaciones del límite en los applets. DISCUSIÓN. En el análisis de la idoneidad didáctica realizado, destaca la importancia de la variable interactividad, por potenciar el desarrollo de la mayoría de las imágenes conceptuales del límite. También resulta positivo el uso de una mayor cantidad de sistemas de representación del límite en un applet, pues favorece el desarrollo de varias acciones en dichos sistemas de representación.
Palabras clave: Enfoque ontosemiótico, Educación matemática, Usos de la tecnología en educación, Recursos educativos.
Desde su creación, GeoGebra ha experimentado un éxito sin precedentes entre los docentes de matemáticas, llegando a contar con cientos de miles de usuarios mensuales y con más de un millón de actividades en su repositorio (Hohenwarter y Lavicza, 2007Hohenwarter, M. y Lavicza, Z. (2007). Mathematics teacher development with ICT: towards an International GeoGebra Institute. Proceedings of the British Society for Research into Learning Mathematics, 27(3), 49-54.). Sin embargo, posiblemente a consecuencia de este éxito, no existe ningún proceso de revisión de expertos que filtre de algún modo los applets depositados en el repositorio oficial de GeoGebra. Esto implica que, en la práctica, muchos de ellos estén incompletos y algunos puedan eventualmente presentar errores matemáticos.
Además, hemos de tener en cuenta que estos applets son frecuentemente utilizados como recursos formativos por personas distintas a quienes los han creado. Por ello, son necesarias investigaciones que los analicen desde un punto de vista didáctico y que ofrezcan a los docentes estrategias para analizar y evaluar dichos applets. De este modo, los usuarios podrán tomar una decisión respecto a su utilización basada en criterios matemáticos y didácticos. El desempeño docente en el uso de otras herramientas como vídeos educativos o redes sociales para la enseñanza de las matemáticas ha sido analizado en trabajos como Cid et al. (2018Cid, A. I., Guede, R. y Tolmos, P. (2018). La clase invertida en la formación inicial del profesorado: acercando la realidad del aula de matemáticas. Bordón, Revista de Pedagogía, 70(3), 77-93.) y García et al. (2016García, R., Rebollo-Catalán, A. y García, C. (2016). Relación entre las preferencias de formación del profesorado y su competencia digital en las redes sociales. Bordón, Revista de Pedagogía, 68(2), 137-153. https://doi.org/10.13042/Bordon.2016.68209).
Problemáticas similares surgen en ámbitos como los recursos educativos en línea o los vídeos educativos matemáticos. Así, Turney et al. (2009Turney, C. S. M., Robinson, D., Lee, M. y Soutar, A. (2009). Using technology to direct learning in higher education. The way forward? Active Learning in Higher Education, 10(1), 71-83. https://doi.org/10.1177/1469787408100196) ponen de manifiesto que el uso de tecnología puede provocar que los estudiantes desarrollen estrategias de aprendizaje inadecuadas. Por su parte, Beltrán-Pellicer et al. (2018Beltrán-Pellicer, P., Giacomone, B. y Burgos, M. (2018). Online educational videos according to specific didactics: the case of mathematics / Los vídeos educativos en línea desde las didácticas específicas: el caso de las matemáticas. Culture and Education, 30(4), 633-662. https://doi.org/10.1080/11356405.2018.1524651) identifican carencias recurrentes en su análisis de vídeos de YouTube que pueden interferir con las secuencias didácticas diseñadas por los docentes. Además, se expone que el enfoque ontosemiótico del conocimiento y la instrucción matemáticos (Godino et al., 2007Godino, J. D., Batanero, C. y Font, V. (2007). The onto-semiotic approach to research in mathematics education. ZDM. The International Journal on Mathematics Education, 39(1-2), 127-135. https://doi.org/10.1007/s11858-006-0004-1) permite abordar la problemática planteada desde el concepto de idoneidad didáctica (Burgos et al., 2020Burgos, M., Beltrán-Pellicer, P. y Godino, J. D. (2020). La cuestión de la idoneidad de los vídeos educativos de matemáticas: una experiencia de análisis con futuros maestros de educación primaria. Revista Española de Pedagogía, 78(275), 27-49. https://doi.org/10.22550/REP78-1-2020-07; Godino, 2013Godino, J. D. (2013). Indicadores de la idoneidad didáctica de procesos de enseñanza y aprendizaje de las matemáticas. Cuadernos de Investigación y Formación en Educación Matemática, 11, 111-132.).
Considerando la situación expuesta, en este trabajo pretendemos analizar algunas características fundamentales de applets dedicados al trabajo con el concepto de límite funcional depositados en el repositorio de GeoGebra. Se ha elegido este objeto matemático debido a su importancia (Claros et al., 2007Claros, F. J., Sánchez, M. T. y Coriat, M. (2007). Fenómenos que organizan el límite. PNA, 1(3), 125-137.), así como al potencial uso de GeoGebra en su enseñanza y aprendizaje (Hutkemri, 2014Hutkemri, E. Z. (2014). Impact of using GeoGebra on students’ conceptual and procedural knowledge of limit function. Mediterranean Journal of Social Sciences, 5(23), 873-881. https://doi.org/10.5901/mjss.2014.v5n23p873). En particular, los objetivos específicos de este trabajo son:
Estos dos objetivos y sus posibles influencias mutuas, junto con características relacionadas con la interactividad de los applets considerados, nos permiten estudiar aspectos clave relacionados con la idoneidad epistémica de estos recursos.
Este trabajo está estructurado de la siguiente manera: en el siguiente apartado se expone el marco teórico y contexto de la investigación. Posteriormente, se presenta el método seguido en el estudio realizado, así como las variables consideradas. Después se muestran los resultados obtenidos en el análisis realizado. Finalmente, se presentan las conclusiones y una discusión sobre la investigación llevada a cabo.
El enfoque ontosemiótico (EOS) del conocimiento y la instrucción matemáticos (Godino et al., 2007Godino, J. D., Batanero, C. y Font, V. (2007). The onto-semiotic approach to research in mathematics education. ZDM. The International Journal on Mathematics Education, 39(1-2), 127-135. https://doi.org/10.1007/s11858-006-0004-1) considera seis tipos de objetos matemáticos primarios, cuya interacción permite describir la actividad matemática:
Entre otros muchos aspectos, el EOS ofrece herramientas útiles para el análisis de recursos digitales para la enseñanza de las matemáticas (como los applets de GeoGebra considerados) y pone de manifiesto, en particular, la necesidad de analizar la idoneidad didáctica de los recursos utilizados por el docente.
La noción de idoneidad didáctica, así como sus dimensiones, criterios y principales indicadores, se encuentra desarrollada en Godino (2013Godino, J. D. (2013). Indicadores de la idoneidad didáctica de procesos de enseñanza y aprendizaje de las matemáticas. Cuadernos de Investigación y Formación en Educación Matemática, 11, 111-132.). Este constructo se define como “el grado en que un proceso de instrucción reúne ciertas características que permiten calificarlo como óptimo o adecuado, siendo el principal criterio la adaptación entre los significados personales construidos por los alumnos (aprendizaje) y los significados institucionales, ya sean pretendidos o implementados (enseñanza), considerando la influencia del entorno” (Burgos et al., 2020Burgos, M., Beltrán-Pellicer, P. y Godino, J. D. (2020). La cuestión de la idoneidad de los vídeos educativos de matemáticas: una experiencia de análisis con futuros maestros de educación primaria. Revista Española de Pedagogía, 78(275), 27-49. https://doi.org/10.22550/REP78-1-2020-07, pp. 29-30). Este proceso de instrucción debe articular de manera coherente y sistemática seis componentes: epistémica, cognitiva, interaccional, mediacional, afectiva y ecológica (Godino et al., 2007Godino, J. D., Batanero, C. y Font, V. (2007). The onto-semiotic approach to research in mathematics education. ZDM. The International Journal on Mathematics Education, 39(1-2), 127-135. https://doi.org/10.1007/s11858-006-0004-1). La noción de idoneidad didáctica, en sus distintas dimensiones, es útil tanto en el diseño como en la valoración de los procesos de enseñanza y aprendizaje de las matemáticas (Godino et al., 2019Godino, J. D., Batanero, C. y Font, V. (2019). The onto-semiotic approach: implications for the prescriptive character of didactics. For the Learning of Mathematics, 39(1), 38-43. https://www.jstor.org/stable/26742011).
La idoneidad epistémica hace referencia a la “representatividad del significado institucional implementado o pretendido, respecto de un significado de referencia” (Godino et al., 2007Godino, J. D., Batanero, C. y Font, V. (2007). The onto-semiotic approach to research in mathematics education. ZDM. The International Journal on Mathematics Education, 39(1-2), 127-135. https://doi.org/10.1007/s11858-006-0004-1, p. 133). A su vez, Godino et al. (2012Godino, J. D., Rivas, H. y Arteaga, P. (2012). Inferencia de indicadores de idoneidad didáctica a partir de orientaciones curriculares. Práxis Educativa, 7(2), 331-354.) señalan los distintos componentes de la idoneidad epistémica, entre los que cabe destacar los lenguajes y las reglas (definiciones, proposiciones y procedimientos). Estos mismos autores proporcionan además indicadores para cada uno de estos componentes. En el caso de las reglas, se proponen indicadores tales como que “las definiciones y procedimientos sean claros y correctos” o que “se presentan los enunciados y procedimientos fundamentales del tema adaptados al nivel educativo dado”. En lo relativo a los lenguajes, uno de estos indicadores es el uso de “un amplio repertorio de representaciones (materiales, icónicas y simbólicas) para modelizar problemas e ideas matemáticas, analizando la pertinencia y potencialidad de uno u otro tipo de representación y realizando procesos de traducción entre las mismas” (Godino et al., 2012Godino, J. D., Rivas, H. y Arteaga, P. (2012). Inferencia de indicadores de idoneidad didáctica a partir de orientaciones curriculares. Práxis Educativa, 7(2), 331-354., p. 348).
Por otro lado, el concepto de límite es fundamental en el ámbito del análisis, y las dificultades que los estudiantes parecen encontrar para su comprensión se deben, en parte, a que esta implica la articulación de multitud de elementos relacionados con aspectos como su existencia, su carácter estático o dinámico, etc., que “no pueden ser generados puramente a partir de su definición matemática” (Cornu, 2002Cornu, B. (2002). Limits. En D. Tall (ed.), Advanced mathematical thinking (pp. 153-166). Springer. https://doi.org/10.1007/0-306-47203-1_10, p. 153). Asimismo, esta complejidad implica que los estudiantes puedan formarse distintas imágenes o modelos del concepto de límite, que no siempre resultan adecuados (Williams, 1991Williams, S. R. (1991). Models of limit held by college calculus students. Journal for Research in Mathematics Education, 22(3), 219-236. https://doi.org/10.2307/749075; Contreras y García, 2011Contreras, Á. y García, M. (2011). Significados pretendidos y personales en un proceso de estudio con el límite funcional. Revista Latinoamericana de Investigación en Matemática Educativa, 14(3), 277-310.) y que pueden variar en función de si se trata de un límite finito o infinito, o de si se considera en un punto o en el infinito (Sánchez-Compaña, 2012Sánchez-Compaña, T. (2012). Límite finito de una función en un punto: fenómenos que organiza [Tesis Doctoral, Universidad de Granada] Repositorio Institucional UG. http://hdl.handle.net/10481/23782).
Siguiendo el trabajo de Tall y Vinner (1981Tall, D. y Vinner, S. (1981). Concept image and concept definition in mathematics with particular reference to limits and continuity. Educational Studies in Mathematics, 12(2), 151-169. https://doi.org/10.1007/BF00305619), Przenioslo (2004Przenioslo, M. (2004). Images of the limit of function formed in the course of mathematical studies at the university. Educational Studies in Mathematics, 55, 103-132. https://doi.org/10.1023/B:EDUC.0000017667.70982.05, p. 104) considera la noción de imagen conceptual como “la estructura cognitiva que contiene todos los tipos de asociaciones y concepciones relacionadas con un concepto […] incluyendo intuiciones, elementos de comprensión formal, pautas establecidas, procedimientos aplicados a distintas situaciones y estrategias operacionales”. En su estudio empírico con estudiantes universitarios, se identifican seis grandes grupos de imágenes conceptuales asociadas al límite de una función que se identifican con base en lo que la autora denomina su elemento clave. Así, distingue entre imágenes conceptuales focalizadas en la idea de:
Evidentemente, estos elementos clave no son excluyentes entre sí, de tal modo que la idea de límite de muchos estudiantes combina concepciones asociadas con más de uno de ellos. Sin embargo, cabe resaltar que Przenioslo (2004Przenioslo, M. (2004). Images of the limit of function formed in the course of mathematical studies at the university. Educational Studies in Mathematics, 55, 103-132. https://doi.org/10.1023/B:EDUC.0000017667.70982.05) considera como “eficientes” únicamente las dos primeras, entendiendo por eficiente aquella imagen conceptual que permite al estudiante comprender las propiedades y teoremas relacionados con el límite de una función, así como comprender sus vínculos con otras nociones matemáticas.
A menudo la actividad matemática necesita utilizar diferentes sistemas de representación semiótica que se puedan utilizar libremente según la tarea que realizar. Aunque algunos procesos son más fáciles en un sistema semiótico que en otro, o incluso pueden realizarse en uno solo, lo cierto es que en muchos casos no se utiliza un único sistema de representación, sino que se precisan al menos dos, bien sea de manera implícita o explícita (Duval, 2006Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics, 61(1), 103-131. https://doi.org/10.1007/s10649-006-0400-z). A este respecto, Socas (2007Socas, M. (2007). Dificultades y errores en el aprendizaje de las matemáticas. Análisis desde el enfoque lógico semiótico. En M. Camacho, P. Flores y P. Bolea (eds.), Investigación en educación matemática XI (pp. 19-52). SEIEM.) señala distintos tipos de acciones que pueden llevarse a cabo cuando se utilizan distintas representaciones:
La realización de estas acciones en el contexto de un objeto matemático concreto caracteriza, en cierto modo, la actividad matemática y su presencia es, como hemos visto, un indicador de idoneidad epistémica. De hecho, el lenguaje matemático surge asociado a la representación de los objetos matemáticos y a su dinámica en y entre los registros semióticos (Pecharromán, 2013Pecharromán, C. (2013). Naturaleza de los objetos matemáticos: representación y significado. Enseñanza de las Ciencias, 31(3), 121-134. https://doi.org/10.5565/rev/ec/v31n3.931).
En el contexto que nos ocupa, Blázquez y Ortega (2001Blázquez, S. y Ortega, T. (2001). Los sistemas de representación en la enseñanza del límite. Revista Latinoamericana de Investigación en Matemática Educativa, 4(3), 219-236., p. 226) sostienen que “la utilización de distintos registros […] mejora la comprensión del concepto de límite”. Estos autores consideran cuatro sistemas de representación fundamentales asociados al concepto de límite: verbal, numérico, gráfico y algebraico. Cada uno de ellos tiene unas potencialidades y limitaciones que pueden mostrar u ocultar distintas imágenes conceptuales de la idea de límite (Palomino et al., 2009Palomino, J., Hurtado, J. y Barrios, E. (2009). Dificultades en los procesos de enseñanza aprendizaje del concepto de límite y su relación con los sistemas de representación. En VI Encuentro Internacional de Matemáticas - EIMAT 2009 (pp. 187-208). Universidad del Atlántico.). Por otro lado, algunas investigaciones (Ward et al., 2013Ward, E., Inzunsa, S., Hernández, S. y López, F. (2013). Conceptualización y uso de representaciones sobre el concepto de límite en docentes de bachillerato. En A. Berciano, G. Gutiérrez, A. Estepa y N. Climent (eds.), Investigación en educación matemática XVII (pp. 523-534). SEIEM. ) han señalado que las transformaciones externas entre distintos sistemas de representación parecen ser las acciones que conllevan una mayor dificultad para los docentes.
El uso de software como GeoGebra facilita que los estudiantes trabajen simultáneamente con diversos sistemas de representación y que actúen sobre ellos en un contexto de cálculo diferencial (Caligaris et al., 2015Caligaris, M. G., Schivo, M. E. y Romiti, M. R. (2015). Calculus & GeoGebra, an interesting partnership. Procedia-Social and Behavioral Sciences, 174, 1183-1188. https://doi.org/10.1016/j.sbspro.2015.01.735). La utilización de este software, especialmente por sus características dinámicas e interactivas, puede contribuir a mejorar la comprensión del concepto de límite (Sari, 2017Sari, P. (2017). GeoGebra as a means for understanding limit concepts. Southeast Asian Mathematics Education Journal, 7(2), 71-84. https://doi.org/10.46517/seamej.v7i2.55). Por tanto, a la hora de analizar los applets de GeoGebra, resulta primordial atender al concepto de interactividad de dichos recursos. En este trabajo adoptamos el enfoque de Roussou et al. (2006Roussou, M., Oliver, M. y Slater, M. (2006). The virtual playground: an educational virtual reality environment for evaluating interactivity and conceptual learning. Virtual Reality, 10(3-4), 227-240. https://doi.org/10.1007/s10055-006-0035-5, p. 2), que definen la interactividad como “la capacidad de moverse libremente por un entorno virtual, experimentarlo de primera mano y desde múltiples puntos de vista, modificar sus elementos, controlar parámetros o de responder al feedback ofrecido por el sistema”.
Teniendo en cuenta los objetivos señalados anteriormente, se ha abordado un estudio de tipo exploratorio y fundamentalmente descriptivo (Leavy, 2017Leavy, P. (2017). Research design: quantitative, qualitative, mixed methods, arts-based, and community-based participatory research approaches. The Guilford Press.).
Selección de la muestra
Se ha optado por realizar un muestreo de tipo intencional, purposeful sampling en la terminología de Creswell (2002Creswell, J. W. (2002). Educational research: planning, conducting, and evaluating quantitative and qualitative research. Pearson., p. 206). Se trata de un tipo de muestreo no probabilístico en el que se seleccionan los elementos de la muestra con el fin de obtener información útil para la comprensión del fenómeno estudiado.
Así, se realizó una consulta el 8 de mayo de 2021 en el apartado de materiales de la web de GeoGebra [1], haciendo uso de la herramienta de búsqueda en forma de grafo y siguiendo la ruta “Matemáticas → Cálculo → Límites”. De este modo, se seleccionaron inicialmente los 150 primeros applets. Se eligieron los primeros porque se pretendía considerar la situación de un docente que accede al repositorio en busca de recursos para su clase. Todos los recursos elegidos eran applets individuales y no libros.
A continuación, se realizó una primera revisión de los applets para eliminar aquellos que no proporcionaran información útil para la investigación. En particular, se eliminaron los applets que no abordaban única y específicamente el concepto de límite de una función real de variable real en un punto o en el infinito (algunos trataban el límite de sucesiones, la derivabilidad, el límite de funciones de varias variables, etc.). De igual forma, se descartaron aquellos applets que resultaban meramente expositivos, es decir, que no hacían uso de las funcionalidades dinámicas de GeoGebra (Hohenwarter et al., 2009Hohenwarter, J., Hohenwarter, M. y Lavicza, Z. (2009). Introducing dynamic mathematics software to secondary school teachers: the case of GeoGebra. Journal of Computers in Mathematics and Science Teaching, 28(2), 135-146.).
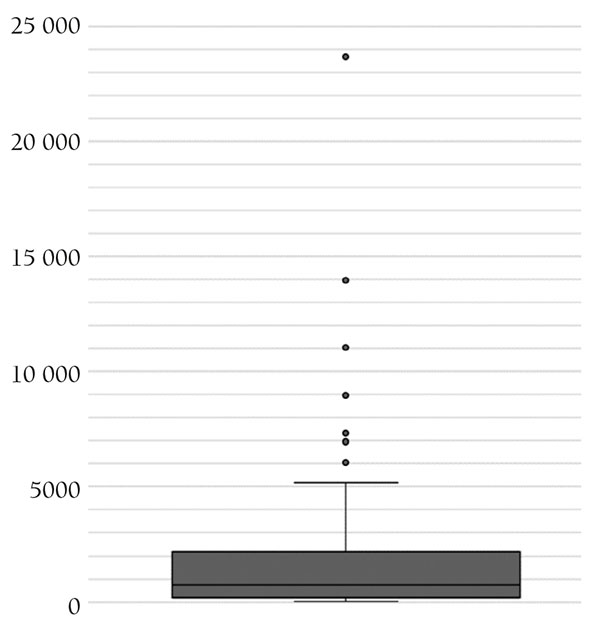
Este proceso de cribado de datos conllevó el descarte de 49 applets. Por lo tanto, el estudio finalmente se realizó con los 101 applets restantes, que se consideró una cantidad suficiente para los objetivos marcados. El número medio de visualizaciones de estos applets era 1882. Aunque el objetivo no era la selección de los applets con más visualizaciones (puesto que, además, estos no aparecen ordenados por el número de visualizaciones tras una búsqueda), sí que hay applets con un gran número de visualizaciones entre los elegidos (ver figura 1).
|
Figura 1. Número de visualizaciones de los applets analizados 
|
Análisis de los datos
El análisis se llevó a cabo con base en cinco variables, adoptando un enfoque deductivo en el que las categorías se derivan del marco teórico. En la tabla 1 se detallan dichas variables, las categorías correspondientes a cada una de ellas y los criterios considerados para la clasificación de los applets.
| Tabla 1. Variables y categorías para el análisis de los applets y criterios de asignación | ||||||||||||||||||||||||||||||||||||||||||||||
|
El análisis realizado, de carácter fundamentalmente cuantitativo, se ha llevado a cabo en dos fases. En la primera se han analizado las características de los applets, clasificando cada uno de ellos en función de las variables y categorías de la tabla 1. En la segunda se han analizado algunos de los posibles vínculos existentes entre las variables consideradas.
Para abordar algunas de las posibles amenazas, tanto internas como externas, a la credibilidad que puede aparecer en relación con este tipo de estudios (Onwuegbuzie y Leech, 2007Onwuegbuzie, A. J. y Leech, N. L. (2007). Validity and qualitative research: an oxymoron? Quality & Quantity, 41(2), 233-249. https://doi.org/10.1007/s11135-006-9000-3), y contribuir a la validez de los resultados, se orquestó un proceso de triangulación de investigadores (Flick, 2004Flick, U. (2004). Triangulation in qualitative research. En U. Flick, E. Von Kardoff e I. Steinke (eds.), A companion to qualitative research (pp. 178-183). SAGE. https://doi.org/10.4135/9781849209441.n7). La muestra se dividió en tres subconjuntos y cada uno de ellos fue analizado y codificado por dos de los investigadores del equipo. En aquellos casos en los que surgieron discrepancias entre ambos, se llegó a una decisión colegiada con la intervención del investigador restante. A través de este proceso se dio lugar a los criterios mencionados en la tabla 1.
Características de los applets
En primer lugar, abordamos un análisis descriptivo de los applets considerados. En particular, estudiamos las características de estos según las variables descritas en la tabla 1.
Tipo de límite
Analizamos el tipo de límite que se aborda en cada uno de los applets considerados, es decir, si se estudian límites puntuales o límites en el infinito.
Se observa un claro predominio de applets centrados únicamente en el límite en un punto frente al límite en el infinito. La figura 2 muestra que menos del 10% de los applets se centran de forma exclusiva en el límite en el infinito, mientras que en torno a un 60% se centran únicamente en el límite en un punto. Menos de la tercera parte de los applets abordan conjuntamente ambos tipos de límites.
|
Figura 2. Tipo de límite abordado en los applets 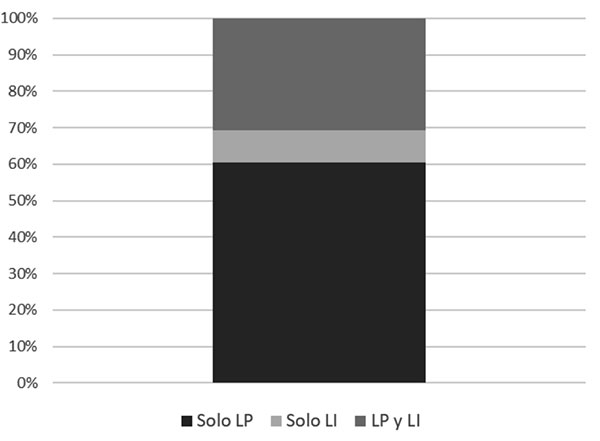
|
Interactividad
De los 101 applets analizados, 15 no se ajustan a la definición de interactividad dada por Roussou et al. (2006Roussou, M., Oliver, M. y Slater, M. (2006). The virtual playground: an educational virtual reality environment for evaluating interactivity and conceptual learning. Virtual Reality, 10(3-4), 227-240. https://doi.org/10.1007/s10055-006-0035-5). El porcentaje de estos applets no interactivos (14.85%) resulta relativamente elevado.
En la figura 3 se presentan los tipos de interactividad de los 86 applets en los que esta se da. La modificación de elementos y el control de parámetros son los rasgos mayoritarios entre los applets interactivos, con una presencia similar. Menos de 20 de los applets interactivos permiten dar respuesta en ellos a las cuestiones planteadas.
|
Figura 3. Categorías relativas a la interactividad de los applets 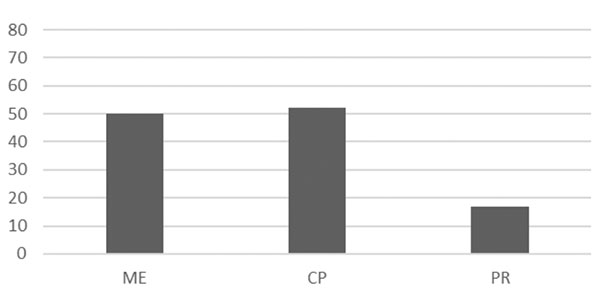
|
Resulta relevante estudiar la presencia conjunta en los applets de dos o más categorías relativas a la interactividad (véase figura 4). Como podemos apreciar, el número de applets que presenta al menos dos categorías relativas a la interactividad es bajo.
|
Figura 4. Presencia de dos categorías relativas a la interactividad 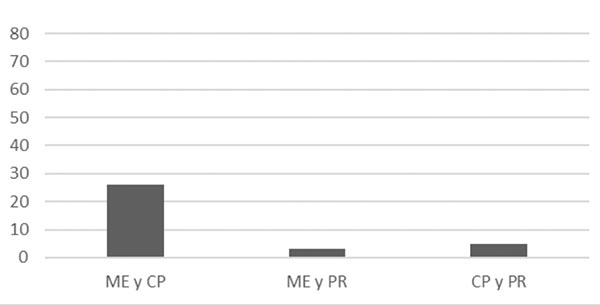
|
Como cabía esperar, la mayor frecuencia se corresponde con aquellos applets en los que se pueden modificar elementos y cambiar parámetros de manera simultánea. Por otro lado, aquellos applets que han sido diseñados para poder dar una respuesta apenas permiten modificar elementos ni controlar parámetros.
Finalmente, tan solo ha sido posible identificar un applet que satisface las tres condiciones propias de la definición de interactividad utilizada.
Imagen conceptual
En la figura 5 se presentan las frecuencias con las que cada una de las imágenes conceptuales consideradas aparece en los applets analizados.
|
Figura 5. Imágenes conceptuales fomentadas por los applets 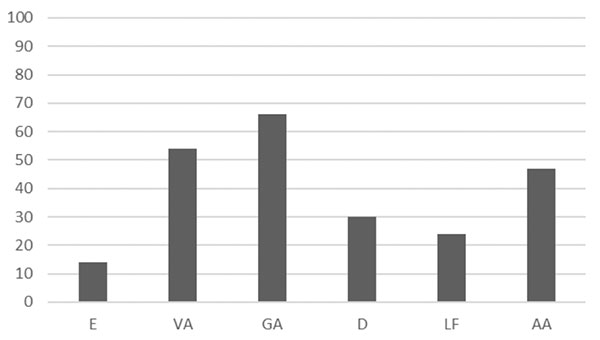
|
Los applets analizados contribuyen mayoritariamente a la construcción de la imagen conceptual del límite de una función centrada en la idea de “gráfica que se aproxima”, seguida de las imágenes conceptuales centradas en las ideas de “valores que se aproximan” y de “aproximación algorítmica esquemática”. Observamos que tan solo 14 de los applets promueven una imagen conceptual centrada en la idea de “entorno”.
Al restringirse a las imágenes conceptuales eficientes, centradas en las ideas de “entorno” y de “valores que se aproximan”, se ha identificado únicamente un applet en el que se promueven ambas imágenes conceptuales de manera simultánea. Sin embargo, se ha observado que 39 de los applets promueven únicamente imágenes conceptuales consideradas ineficientes.
Cabe mencionar que se ha identificado un applet que no ha podido clasificarse de acuerdo con estas imágenes conceptuales asociadas a la noción de límite de una función.
Sistemas de representación
La presencia de los distintos sistemas de representación considerados se muestra en la figura 6. Como puede apreciarse, existe un predominio de las representaciones gráficas y algebraicas frente a las numéricas y verbales, siendo esta última claramente minoritaria.
|
Figura 6. Representaciones del límite utilizadas en los applets 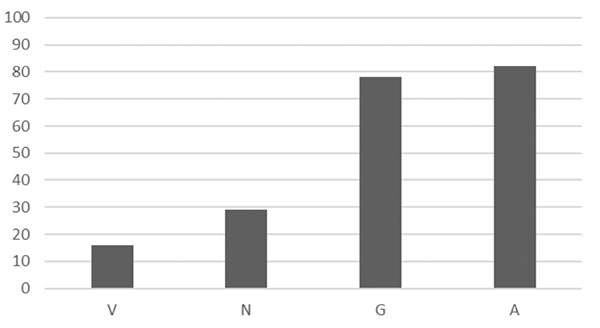
|
En la tabla 2 se presenta, para cada situación (considerando el número de sistemas de representación utilizados), la frecuencia de cada representación usada, de manera aislada o conjunta.
| Tabla 2. Applets que presentan alguna representación del límite | ||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
De los 101 applets analizados, 32 hacían uso de un único sistema de representación (ver tabla 2). En estos casos, no hay una preferencia clara entre el sistema de representación algebraico o gráfico. Además, las representaciones verbal y numérica nunca se utilizan de manera aislada.
En los 69 applets restantes, se utiliza más de un sistema de representación de forma combinada. Lo más habitual es encontrar la combinación de dos sistemas de representación. Cuando esto sucede, en casi el 77% de los casos se combinan las representaciones gráfica y algebraica. También resulta destacable el bajo número de applets (inferior al 5%) en el que se han identificado los cuatro posibles sistemas de representación considerados.
Acciones
En este apartado se analiza la presencia de las distintas acciones en relación con uno o más sistemas de representación (véase figura 7).
|
Figura 7. Acciones presentes en los applets 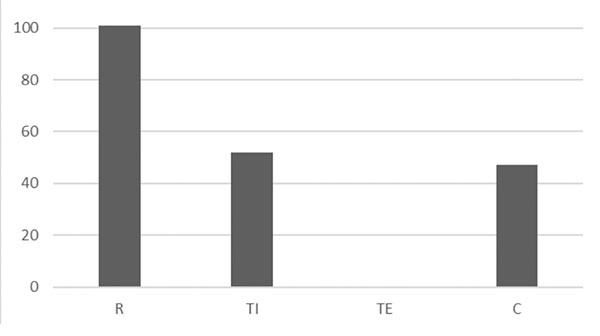
|
Como cabía esperar, en todos los applets analizados se promueve el reconocimiento de alguno de los elementos propios del límite funcional en algún sistema de representación. Por otro lado, no se ha identificado ningún applet en el que se realicen transformaciones externas entre distintos sistemas de representación. En algo más de la mitad de los applets se realizan transformaciones internas dentro de un mismo sistema de representación y en casi la mitad se lleva a cabo un proceso de coordinación entre sistemas de representación del límite.
Un buen número de los applets considerados promueven más de una acción vinculada a los sistemas de presentación que utilizan (véase figura 8). Evidentemente, teniendo en cuenta la figura 7, en aquellos applets en los que solo se identifica una única acción, esta consiste en el reconocimiento de un objeto o de alguno de sus elementos en un sistema de representación concreto.
|
Figura 8. Cantidad de acciones identificadas en los applets 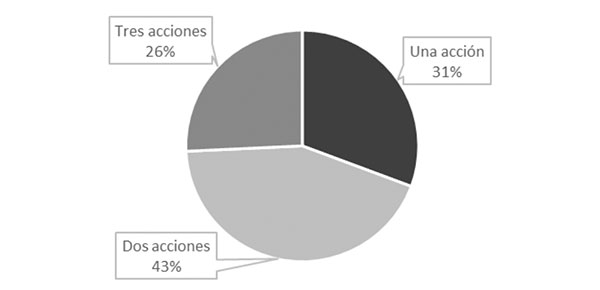
|
Finalmente, solo la cuarta parte de los applets involucran tres acciones. En este caso, dado que en ninguno de los applets se desarrollan transformaciones externas, se trata del reconocimiento de un objeto, de transformaciones internas en un sistema de representación y de la coordinación entre distintos sistemas de representación del límite funcional.
Influencia del carácter interactivo
Se analiza ahora la posible influencia de la interactividad de los applets sobre el resto de las variables analizadas. Para ello, se debe considerar que, de los 101 applets analizados, se han clasificado 86 como interactivos, mientras que los 15 restantes son no interactivos (apartado “Interactividad”).
Tipo de límite
En la figura 9 se observa la distribución del tipo de límite, puntual o en el infinito, considerado en cada applet en función de su carácter interactivo o no. La interactividad de los applets no parece ser una condición relevante para el estudio de un tipo de límite u otro.
|
Figura 9. Tipo de límite abordado en función de la interactividad de los applets 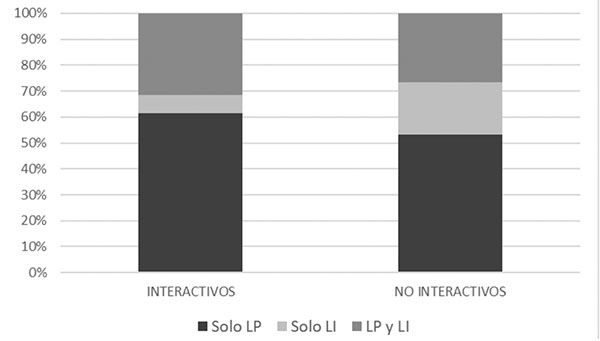
|
Imagen conceptual
En la figura 10 se observa la distribución de las imágenes conceptuales promovidas por los applets en función de su carácter interactivo o no.
|
Figura 10. Vínculo entre la interactividad y las imágenes conceptuales 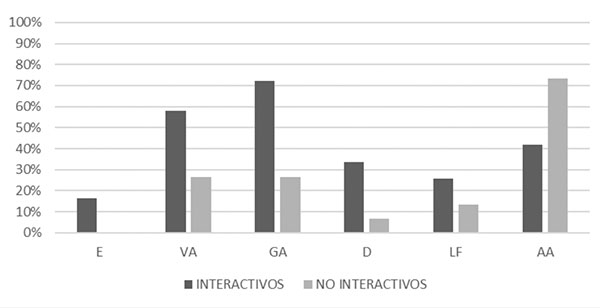
|
Respecto a las imágenes conceptuales, se observa que la interactividad resulta decisiva para el desarrollo de la imagen conceptual centrada en la idea de “entorno” (E), ya que todos los applets identificados que promueven esta imagen conceptual son interactivos.
En general, se aprecia que el porcentaje de applets interactivos que fomentan cada una de las imágenes conceptuales es claramente superior al de applets no interactivos, con la única excepción de la imagen conceptual centrada en la idea de “aproximación algorítmica esquemática”.
Sistemas de representación
En la figura 11 se observa la distribución de los sistemas de representación utilizados en los applets en función de su carácter interactivo o no.
|
Figura 11. Representaciones utilizadas en función de la interactividad de los applets 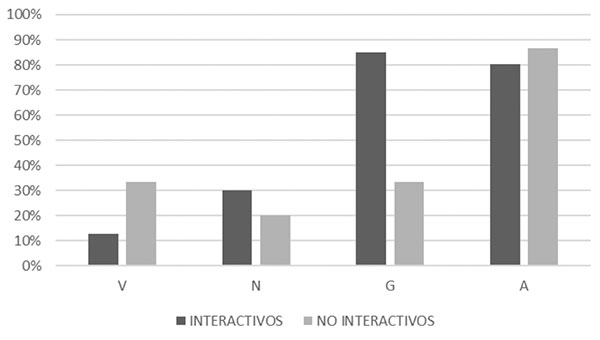
|
Se observa cómo la interactividad se convierte en un aspecto muy importante que favorece la utilización del registro gráfico. También se aprecia que los applets no interactivos tienen mayor predisposición a la utilización del registro verbal. Finalmente, el uso de la representación algebraica y numérica del límite no parece depender de la interactividad de los applets, ya que en ambos casos aparecen porcentajes similares.
En la tabla 3 se consideran, además de los sistemas de representación utilizados, la cantidad de los mismos que aparecen en cada applet.
| Tabla 3. Cantidad de representaciones utilizadas en función de la interactividad | |||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
El análisis de la cantidad de registros que se utilizan para exponer el límite de una función muestra una mayor tendencia a emplear una única representación entre los applets no interactivos, haciendo uso en su mayoría de la representación algebraica del límite. Sin embargo, en el caso de los applets interactivos, el uso de la representación gráfica supera por un pequeño porcentaje a la representación algebraica. Por último, en ninguno de los casos se utilizan las representaciones verbal y numérica de manera aislada.
El porcentaje de applets en los que se hace uso de dos representaciones del límite de una función son similares en ambos casos. No obstante, en la gran mayoría de los applets interactivos, se combinan las representaciones gráfica y algebraica, algo que no sucede cuando se trata de applets no interactivos. Respecto al uso de tres sistemas de representación, esto sucede con un porcentaje mucho mayor en el caso de los applets interactivos.
Acciones
La figura 12 recoge la distribución de las distintas acciones fomentadas entre los sistemas de representación utilizados en los applets, en función de su carácter interactivo o no.
|
Figura 12. Influencia de la interactividad de los applets en las acciones 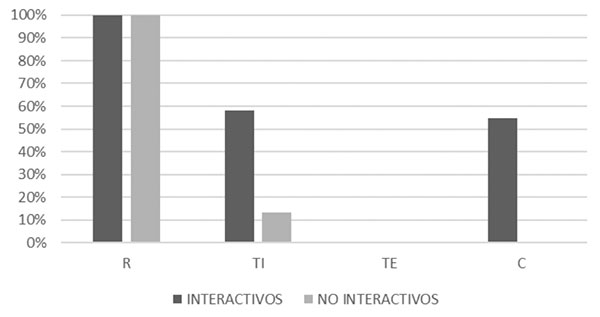
|
Los applets no interactivos se limitan casi exclusivamente al reconocimiento de alguno de los elementos del límite funcional en algún sistema de representación. La realización de transformaciones internas dentro de un sistema de representación y la coordinación entre distintos sistemas de representación son prácticamente exclusivas de los applets interactivos.
Como en la sección anterior, se ha estudiado la posibilidad de realizar varias acciones en un mismo applet (véase tabla 4).
| Tabla 4. Acciones en función de la interactividad | ||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
El porcentaje de applets en los que solo se puede realizar una acción es muy superior en el caso de los no interactivos. Por su parte, la situación es la contraria en el caso de los applets que permiten ejecutar dos o tres acciones. De hecho, ningún applet no interactivo permite realizar tres acciones simultáneamente. Se observa que en ninguno de los applets no interactivos consultados se lleva a cabo la acción de coordinación entre sistemas de representación.
Influencia de la variedad de sistemas de representación
En este se analiza la influencia que tiene la variedad de sistemas de representación del límite de una función utilizados en los applets sobre las acciones que se pueden llevar a cabo dentro de dicho applet.
Tal y como vimos en el apartado “Sistemas de representación”, 32 de los applets analizados hacían uso de un único sistema de representación. En la figura 13 mostramos las acciones identificadas en este caso.
|
Figura 13. Sistemas de representación y acciones 
|
Dado que estos applets tan solo utilizan un sistema de representación del límite de una función, no puede haber transformaciones externas ni coordinación entre sistemas de representación. Sin embargo, merece la pena señalar que el número de applets en los que se llevan a cabo transformaciones internas dentro del sistema de representación considerado (ya sea gráfico o algebraico, véase tabla 2) no llega a la mitad.
Cuando se analizan los applets que utilizan dos sistemas de representación del límite, dejando de lado el reconocimiento, que se da siempre, observamos que menos de la mitad fomentan la realización de transformaciones internas, siendo mayor el porcentaje de applets en los que se hace uso de la coordinación entre estos dos sistemas de representación.
En el caso de applets en los que se emplean más de tres sistemas de representación del límite, la presencia relativa de las transformaciones internas en un sistema de representación y de la coordinación entre sistemas de representación es considerablemente mayor que en los casos en los que se consideran una o dos representaciones del límite.
En la figura 14 se observa que, al considerar los applets que utilizan dos representaciones del límite, la proporción de applets que permiten realizar una única acción se reduce considerablemente respecto de aquellos applets que emplean una única representación. Destaca también el hecho de que la presencia de applets que posibilitan efectuar dos acciones es similar en ambos casos, si bien aumenta considerablemente la frecuencia con la que los applets permiten realizar tres acciones.
|
Figura 14. Sistemas de representación y número de acciones 
|
Como ya hemos visto en el marco teórico, en el estudio de las imágenes conceptuales que los estudiantes construyen sobre la noción de límite de una función, Przenioslo (2004Przenioslo, M. (2004). Images of the limit of function formed in the course of mathematical studies at the university. Educational Studies in Mathematics, 55, 103-132. https://doi.org/10.1023/B:EDUC.0000017667.70982.05) considera que aquellas centradas en las ideas de “entorno” y de “valores que se aproximan” son eficientes, mientras que el resto eran consideradas ineficientes. Entre las imágenes conceptuales eficientes, se observa que los applets analizados promueven ampliamente la imagen conceptual de “valores que se aproximan”, pero la centrada en la idea de “entorno” es la menos fomentada. Por otro lado, entre las imágenes conceptuales ineficientes, las de “gráfica que se aproxima” y “aproximación algorítmica esquemática” son ampliamente promovidas. Además, las imágenes asociadas a las ideas de “estar definida en el punto” y “el límite en el punto coincide con la función en el punto” también son promovidas, aunque en menor medida. A la hora de desarrollar las diferentes imágenes conceptuales de la noción de límite, se ha observado que la mayor parte de los applets eran interactivos, frente a los no interactivos, donde las imágenes conceptuales aparecían con menos frecuencia (a excepción de la imagen centrada en la idea de “aproximación algorítmica esquemática”, donde la tendencia se invertía). Por lo tanto, como cabía esperar, la interactividad parece ser una buena elección a la hora de desarrollar dichas imágenes conceptuales eficientes.
Socas (2007Socas, M. (2007). Dificultades y errores en el aprendizaje de las matemáticas. Análisis desde el enfoque lógico semiótico. En M. Camacho, P. Flores y P. Bolea (eds.), Investigación en educación matemática XI (pp. 19-52). SEIEM.) resalta la necesidad de diseñar actividades que proporcionen los cuatro tipos de acciones al utilizar distintas representaciones (reconocimiento, transformaciones internas, transformaciones externas y coordinación). Sin embargo, no se ha encontrado ningún applet que proporcione transformaciones externas, en consonancia con el resultado obtenido por Ward et al. (2013Ward, E., Inzunsa, S., Hernández, S. y López, F. (2013). Conceptualización y uso de representaciones sobre el concepto de límite en docentes de bachillerato. En A. Berciano, G. Gutiérrez, A. Estepa y N. Climent (eds.), Investigación en educación matemática XVII (pp. 523-534). SEIEM.), donde se afirma que este tipo de acciones son las que más dificultades generan a los docentes. Aunque este tipo de acción sería deseable, su desarrollo puede ser complicado a través de applets de GeoGebra. Cabe destacar que la interactividad de los applets favorece el desarrollo de las acciones de transformación interna dentro de un mismo sistema de representación y de coordinación entre diferentes sistemas de representación. Además, favorece la aparición de dos y hasta tres acciones de manera simultánea en el mismo applet. Mientras que en los applets no interactivos estas acciones disminuyen drásticamente o ni siquiera llegan a aparecer.
Por otro lado, a medida que aumenta la cantidad de sistemas de representación del límite empleados, el porcentaje de applets en los que se realizan transformaciones internas en un sistema de representación y en los que se coordinan distintos sistemas de representación también aumenta. A su vez, el porcentaje de applets que permiten hacer dos y tres acciones también crece, a diferencia del de los applets que tan solo permiten realizar una única acción. Esto parece indicar la existencia de una correlación entre la cantidad de representaciones del límite utilizadas en los applets y el porcentaje de applets que permiten realizar dos o tres acciones entre los sistemas de representación valorados. Por último, considerando que Pecharromán (2013Pecharromán, C. (2013). Naturaleza de los objetos matemáticos: representación y significado. Enseñanza de las Ciencias, 31(3), 121-134. https://doi.org/10.5565/rev/ec/v31n3.931) afirma que la realización de estas acciones en el contexto de un objeto matemático concreto caracteriza en cierto modo la actividad matemática y su presencia es un indicador de idoneidad epistémica, las conclusiones obtenidas confirman lo expuesto por Blázquez y Ortega (2001Blázquez, S. y Ortega, T. (2001). Los sistemas de representación en la enseñanza del límite. Revista Latinoamericana de Investigación en Matemática Educativa, 4(3), 219-236.), cuando afirmaron que “la utilización de distintos registros […] mejora la comprensión del concepto de límite”.
La capacidad de coordinar distintos registros por el estudiante se ve dificultada por el hecho de que el software media ese proceso. Los applets, en muchos casos, requieren de un discurso docente que no está presente en los mismos, de manera que a la hora de utilizarlos en la práctica docente es preciso considerar la idoneidad ecológica presentada por Godino et al. (2007Godino, J. D., Batanero, C. y Font, V. (2007). The onto-semiotic approach to research in mathematics education. ZDM. The International Journal on Mathematics Education, 39(1-2), 127-135. https://doi.org/10.1007/s11858-006-0004-1). En cualquier caso, el aumento en el número de representaciones del límite utilizadas favorece la acción de coordinación en los applets analizados (ver figura 13).
Según Godino et al. (2019Godino, J. D., Batanero, C. y Font, V. (2019). The onto-semiotic approach: implications for the prescriptive character of didactics. For the Learning of Mathematics, 39(1), 38-43. https://www.jstor.org/stable/26742011, p. 42), la didáctica “debe abordar cuestiones […] también prescriptivas y valorativas, propias del conocimiento tecnológico […] debe proporcionar resultados que permitan la acción efectiva sobre una parcela de la realidad: la enseñanza y aprendizaje de la matemática”. En este sentido, la literatura existente tiene claras implicaciones prescriptivas sobre las cualidades que debería tener un applet destinado a la enseñanza del límite de una función. En concreto, se deberían fomentar a través de la interactividad imágenes conceptuales eficientes en un contexto en que se realicen todo tipo de acciones sobre la mayor variedad posible de sistemas de representación. Nuestros resultados parecen indicar que estos cuatro elementos (interactividad, eficiencia de la imagen conceptual, riqueza de sistemas de representación y acciones) van de la mano. Sin embargo, desde un punto de vista valorativo, hemos constatado en la muestra analizada una riqueza relativamente baja de sistemas de representación y de acciones (incluso la ausencia de transformaciones externas) y la presencia comparativamente alta de imágenes conceptuales ineficientes. Estos aspectos implican que los docentes deban ser críticos a la hora de seleccionar recursos online ajenos, así como ser cuidadosos en el diseño de los propios.
Finalmente, en este trabajo nos hemos centrado solo en algunos de los objetos primarios que, según el EOS, permiten describir la actividad matemática. En particular, nos hemos centrado en el lenguaje (a través de los sistemas de representación), en los conceptos (a través de las imágenes conceptuales) y en cierto modo en los procedimientos (a través de las acciones realizadas dentro de los sistemas de representación). Pensamos que puede ser interesante ampliar el análisis a los restantes objetos primarios, desarrollando un instrumento de análisis más completo que nos permita no solo clasificar los applets desde el punto de vista de su idoneidad, sino también realizar actividades de formación basadas en dicho instrumento (Burgos et al., 2020Burgos, M., Beltrán-Pellicer, P. y Godino, J. D. (2020). La cuestión de la idoneidad de los vídeos educativos de matemáticas: una experiencia de análisis con futuros maestros de educación primaria. Revista Española de Pedagogía, 78(275), 27-49. https://doi.org/10.22550/REP78-1-2020-07).
Los autores desean agradecer a los revisores por habernos sugerido algunas referencias y por los comentarios que han contribuido a la mejora de este trabajo.
Este trabajo ha sido parcialmente financiado por el grupo de investigación Didáctica de las Matemáticas y de las Ciencias Experimentales (DIMACE) de UNIR.
El tercer autor ha sido financiado por el grupo Investigación en Educación Matemática (Grupo S60_20R) del Gobierno de Aragón.
| [1] https://www.geogebra.org/materials |
| ○ | Beltrán-Pellicer, P., Giacomone, B. y Burgos, M. (2018). Online educational videos according to specific didactics: the case of mathematics / Los vídeos educativos en línea desde las didácticas específicas: el caso de las matemáticas. Culture and Education, 30(4), 633-662. https://doi.org/10.1080/11356405.2018.1524651 |
| ○ | Blázquez, S. y Ortega, T. (2001). Los sistemas de representación en la enseñanza del límite. Revista Latinoamericana de Investigación en Matemática Educativa, 4(3), 219-236. |
| ○ | Burgos, M., Beltrán-Pellicer, P. y Godino, J. D. (2020). La cuestión de la idoneidad de los vídeos educativos de matemáticas: una experiencia de análisis con futuros maestros de educación primaria. Revista Española de Pedagogía, 78(275), 27-49. https://doi.org/10.22550/REP78-1-2020-07 |
| ○ | Caligaris, M. G., Schivo, M. E. y Romiti, M. R. (2015). Calculus & GeoGebra, an interesting partnership. Procedia-Social and Behavioral Sciences, 174, 1183-1188. https://doi.org/10.1016/j.sbspro.2015.01.735 |
| ○ | Cid, A. I., Guede, R. y Tolmos, P. (2018). La clase invertida en la formación inicial del profesorado: acercando la realidad del aula de matemáticas. Bordón, Revista de Pedagogía, 70(3), 77-93. |
| ○ | Claros, F. J., Sánchez, M. T. y Coriat, M. (2007). Fenómenos que organizan el límite. PNA, 1(3), 125-137. |
| ○ | Contreras, Á. y García, M. (2011). Significados pretendidos y personales en un proceso de estudio con el límite funcional. Revista Latinoamericana de Investigación en Matemática Educativa, 14(3), 277-310. |
| ○ | Cornu, B. (2002). Limits. En D. Tall (ed.), Advanced mathematical thinking (pp. 153-166). Springer. https://doi.org/10.1007/0-306-47203-1_10 |
| ○ | Creswell, J. W. (2002). Educational research: planning, conducting, and evaluating quantitative and qualitative research. Pearson. |
| ○ | Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics, 61(1), 103-131. https://doi.org/10.1007/s10649-006-0400-z |
| ○ | Flick, U. (2004). Triangulation in qualitative research. En U. Flick, E. Von Kardoff e I. Steinke (eds.), A companion to qualitative research (pp. 178-183). SAGE. https://doi.org/10.4135/9781849209441.n7 |
| ○ | García, R., Rebollo-Catalán, A. y García, C. (2016). Relación entre las preferencias de formación del profesorado y su competencia digital en las redes sociales. Bordón, Revista de Pedagogía, 68(2), 137-153. https://doi.org/10.13042/Bordon.2016.68209 |
| ○ | Godino, J. D. (2013). Indicadores de la idoneidad didáctica de procesos de enseñanza y aprendizaje de las matemáticas. Cuadernos de Investigación y Formación en Educación Matemática, 11, 111-132. |
| ○ | Godino, J. D., Batanero, C. y Font, V. (2007). The onto-semiotic approach to research in mathematics education. ZDM. The International Journal on Mathematics Education, 39(1-2), 127-135. https://doi.org/10.1007/s11858-006-0004-1 |
| ○ | Godino, J. D., Batanero, C. y Font, V. (2019). The onto-semiotic approach: implications for the prescriptive character of didactics. For the Learning of Mathematics, 39(1), 38-43. https://www.jstor.org/stable/26742011 |
| ○ | Godino, J. D., Rivas, H. y Arteaga, P. (2012). Inferencia de indicadores de idoneidad didáctica a partir de orientaciones curriculares. Práxis Educativa, 7(2), 331-354. |
| ○ | Hohenwarter, J., Hohenwarter, M. y Lavicza, Z. (2009). Introducing dynamic mathematics software to secondary school teachers: the case of GeoGebra. Journal of Computers in Mathematics and Science Teaching, 28(2), 135-146. |
| ○ | Hohenwarter, M. y Lavicza, Z. (2007). Mathematics teacher development with ICT: towards an International GeoGebra Institute. Proceedings of the British Society for Research into Learning Mathematics, 27(3), 49-54. |
| ○ | Hutkemri, E. Z. (2014). Impact of using GeoGebra on students’ conceptual and procedural knowledge of limit function. Mediterranean Journal of Social Sciences, 5(23), 873-881. https://doi.org/10.5901/mjss.2014.v5n23p873 |
| ○ | Leavy, P. (2017). Research design: quantitative, qualitative, mixed methods, arts-based, and community-based participatory research approaches. The Guilford Press. |
| ○ | Onwuegbuzie, A. J. y Leech, N. L. (2007). Validity and qualitative research: an oxymoron? Quality & Quantity, 41(2), 233-249. https://doi.org/10.1007/s11135-006-9000-3 |
| ○ | Palomino, J., Hurtado, J. y Barrios, E. (2009). Dificultades en los procesos de enseñanza aprendizaje del concepto de límite y su relación con los sistemas de representación. En VI Encuentro Internacional de Matemáticas - EIMAT 2009 (pp. 187-208). Universidad del Atlántico. |
| ○ | Pecharromán, C. (2013). Naturaleza de los objetos matemáticos: representación y significado. Enseñanza de las Ciencias, 31(3), 121-134. https://doi.org/10.5565/rev/ec/v31n3.931 |
| ○ | Przenioslo, M. (2004). Images of the limit of function formed in the course of mathematical studies at the university. Educational Studies in Mathematics, 55, 103-132. https://doi.org/10.1023/B:EDUC.0000017667.70982.05 |
| ○ | Roussou, M., Oliver, M. y Slater, M. (2006). The virtual playground: an educational virtual reality environment for evaluating interactivity and conceptual learning. Virtual Reality, 10(3-4), 227-240. https://doi.org/10.1007/s10055-006-0035-5 |
| ○ | Sánchez-Compaña, T. (2012). Límite finito de una función en un punto: fenómenos que organiza [Tesis Doctoral, Universidad de Granada] Repositorio Institucional UG. http://hdl.handle.net/10481/23782 |
| ○ | Sari, P. (2017). GeoGebra as a means for understanding limit concepts. Southeast Asian Mathematics Education Journal, 7(2), 71-84. https://doi.org/10.46517/seamej.v7i2.55 |
| ○ | Socas, M. (2007). Dificultades y errores en el aprendizaje de las matemáticas. Análisis desde el enfoque lógico semiótico. En M. Camacho, P. Flores y P. Bolea (eds.), Investigación en educación matemática XI (pp. 19-52). SEIEM. |
| ○ | Tall, D. y Vinner, S. (1981). Concept image and concept definition in mathematics with particular reference to limits and continuity. Educational Studies in Mathematics, 12(2), 151-169. https://doi.org/10.1007/BF00305619 |
| ○ | Turney, C. S. M., Robinson, D., Lee, M. y Soutar, A. (2009). Using technology to direct learning in higher education. The way forward? Active Learning in Higher Education, 10(1), 71-83. https://doi.org/10.1177/1469787408100196 |
| ○ | Ward, E., Inzunsa, S., Hernández, S. y López, F. (2013). Conceptualización y uso de representaciones sobre el concepto de límite en docentes de bachillerato. En A. Berciano, G. Gutiérrez, A. Estepa y N. Climent (eds.), Investigación en educación matemática XVII (pp. 523-534). SEIEM. |
| ○ | Williams, S. R. (1991). Models of limit held by college calculus students. Journal for Research in Mathematics Education, 22(3), 219-236. https://doi.org/10.2307/749075 |
Analysis of GeoGebra applets for teaching the limit of a function
INTRODUCTION. The importance of GeoGebra as one of the main tools that offer Mathematics teachers the possibility of working with virtual simulations in their classrooms is indisputable. However, the resources in the official GeoGebra repository do not go through any review process. Therefore, the teacher’s criteria when selecting this type of resource is key for teaching success. Thus, it is necessary to provide teachers with tools to analyze GeoGebra applets for their implementation in the classroom. In particular, this type of resources offers numerous advantages to teach the mathematical concept of the limit of a function. METHOD. In this paper, the didactic suitability of GeoGebra applets for teaching the limit of a function is analyzed. An exploratory and descriptive study has been carried out. The analysis has been carried out using a deductive approach based on five different variables (type of limit, interactivity, conceptual image, representation and action). The analyzed sample, chosen through purposeful sampling, is 150 applets from the official GeoGebra material repository. RESULTS. The results are shown after analyzing the five established variables for each of the studied applets. The influence of interactivity with the rest of the variables is also analyzed, as well as the influence of the number of representations of the limit in the applets. DISCUSSION. In the analysis carried out of the didactic suitability, the importance of the interactivity variable stands out, as it enhances the development of most of the conceptual images of the limit. The use of a greater number of limit representation systems in an applet is also positive, since it favors the development of various actions in said representation systems.
Keywords: Onto-semiotic approach, Mathematics education, Technology uses in education, Educational resources.
Analyse des applets GeoGebra pour l’enseignement de la limite d’une function
INTRODUCTION. L’importance de GeoGebra comme l’un des principaux outils offrant aux professeurs de mathématiques la possibilité de travailler avec des simulations virtuelles dans leurs classes est indiscutable. Cependant, les ressources du dépôt officiel de GeoGebra ne sont pas soumises à aucun processus de révision. Par conséquent, les critères de l’enseignant lors de la sélection de ce type de ressource sont essentiels. Des outils sont nécessaires pour analyser les applets GeoGebra en vue de leur mise en œuvre. En particulier, par rapport à d’autres types d’outils, ce type de ressource offre de nombreux avantages pour l’enseignement du concept mathématique de la limite d’une fonction. MÉTHODE. Cet article analyse l’adéquation didactique des applets GeoGebra pour l’enseignement de la limite d’une fonction. Une étude exploratoire et descriptive a été réalisée. L’analyse a été effectuée en utilisant une approche déductive basée sur cinq variables différentes (type de limite, interactivité, image conceptuelle, représentation et action). L’échantillon analysé, choisi au moyen d’un échantillonnage raisonné, est constitué de 150 applets provenant du dépôt officiel de GeoGebra. RÉSULTATS. Les résultats sont présentés après l’analyse des cinq variables établies pour chacune des applets étudiées. Nous analysons également l’influence de l’interactivité avec le reste des variables, ainsi que l’influence du nombre de représentations de la limite dans les applets. DISCUSSION. Dans l’analyse de l’adéquation didactique effectuée, l’importance de la variable interactivité ressort car elle favorise le développement de la plupart des images conceptuelles de la limite. L’utilisation d’un plus grand nombre de systèmes de représentation de la limite dans une applet est également positive car elle favorise le développement de plusieurs actions dans ces systèmes de représentation.
Mots-clés : Approche onto-sémiotique, Enseignement des mathématiques, U de la technologie dans l’enseignement, Ressources pédagogiques.
Álvaro Barreras Peral (autor de contacto)
Doctor en Matemáticas. Profesor de Matemáticas (Centro Universitario de la Defensa de Zaragoza, 2014-2016). Profesor de Didáctica Matemáticas (UNIR, 2016-actualidad). Director académico de dos másteres en Didáctica de las Matemáticas en UNIR. Investigador principal del grupo de investigación de UNIR Didáctica de las Matemáticas y de las Ciencias Experimentales.
Código ORCID: https://orcid.org/0000-0001-5325-8505
Correo electrónico de contacto: alvaro.barreras@unir.net
Dirección para la correspondencia: Universidad Internacional de La Rioja. Av. de la Paz, 137, 26006 Logroño (La Rioja).
Luis Dubarbie
Licenciado y doctor en Ciencias Matemáticas por la Universidad de Cantabria. Actualmente es profesor de Didáctica de las Matemáticas en la Universidad Internacional de La Rioja (UNIR). Miembro del grupo de investigación Didáctica de las Matemáticas y de las Ciencias Experimentales de UNIR. Publicaciones en el ámbito de las matemáticas y de la didáctica de las matemáticas.
Código ORCID: https://orcid.org/0000-0001-9133-1128
Correo electrónico de contacto: luis.dubarbie@unir.net
Antonio Oller
Licenciado en Ciencias Matemáticas (2004) por la Universidad de Zaragoza y doctor por la Universidad de Valladolid (2012) con una tesis sobre la enseñanza de la proporcionalidad aritmética en educación secundaria. Actualmente es profesor del Centro Universitario de la Defensa de Zaragoza. Ha publicado numerosos trabajos de investigación sobre matemática pura, historia y educación matemática publicados en el ámbito nacional e internacional. Es IP del grupo de referencia Investigación en Educación Matemática (S60_20R) del Gobierno de Aragón.
Código ORCID: https://orcid.org/0000-0002-8191-3199
Correo electrónico de contacto: oller@unizar.es