Figura 1. Desempeño global de los grupos considerados según el ámbito de los ítems
Fuente: elaboración propia.
SUSANA NIETO-ISIDRO, FERNANDO MARTÍNEZ-ABAD Y MARÍA JOSÉ RODRÍGUEZ-CONDE
Universidad de Salamanca (España)
DOI: 10.13042/Bordon.2020.72694
Fecha de recepción: 20/05/2019 • Fecha de aceptación: 20/04/2020
Autora de contacto / Corresponding author: Susana Nieto-Isidro. E-mail: sni@usal.es
INTRODUCCIÓN. Aunque existen diversos estudios sobre los conocimientos matemáticos de los estudiantes que acceden a la universidad en España, son escasos los que abarcan largos periodos de tiempo y tienen en cuenta la legislación de acceso en cada periodo. MÉTODO. Se analizan las respuestas en una prueba objetiva de cálculo básico de 627 estudiantes de nuevo ingreso en 8 titulaciones de ingeniería durante 18 años, de 1999 hasta 2017, siguiendo dos normativas de acceso a la universidad vigentes en las etapas 1999-2009 y 2010-2017. El instrumento aplicado incluyó cuestiones teóricas y prácticas, de las cuales se han seleccionado siete ítems relacionados con logaritmos, exponenciales, derivación e integración. Se realiza un estudio diacrónico agrupando los datos en ocho bienios, cinco con la primera normativa y tres con la segunda, mediante cálculo de proporciones y análisis inferencial, incluyendo el tamaño del efecto. RESULTADOS. Los estudiantes presentan comportamientos estadísticamente diferentes en cada etapa legislativa, y la legislación vigente en 2011-2017 permite la generación de grupos con distintos conocimientos en función de sus elecciones y/o resultados en la Prueba de Acceso a la Universidad. El tipo de contenido matemático de cada ítem seleccionado también es relevante, mostrando mejores resultados en logaritmos y exponenciales, y peores en integración. DISCUSIÓN. Se muestra la gran variabilidad del nivel de conocimientos matemáticos de los alumnos que acceden a estudios de ingeniería y la influencia de la legislación de acceso en estos conocimientos; estos resultados pueden servir de referencia para el diseño de futuras pruebas de acceso a la universidad.
Palabras clave: Acceso a la universidad, Matemáticas, Legislación educativa, Evaluación educativa.
Desde 1999 hasta 2017 han estado en vigor en España dos legislaciones de ámbito nacional para regular la Prueba de Acceso a la Universidad (PAU). En la primera etapa (1999-2009, Ley 30/1974, RD 704/1999, RD 1640/1999, RD 69/2000, RD 1742/2003), todos los estudiantes se examinaban de las mismas materias según el Bachillerato cursado. En las ingenierías, todos los estudiantes de nuevo ingreso se habían examinado de Matemáticas como parte de las materias obligatorias de los Bachilleratos de Ciencias.
En la segunda etapa (2010-2017, RD 1892/2008, RD 558/2010) existía mucha variabilidad sobre las asignaturas de las que se examinaban los estudiantes, con un amplio margen de decisión. Así, el examen de Matemáticas pasaba a ser voluntario, y también existía la posibilidad de aprobar la PAU sin haber superado ese examen. De esta manera se generaba una gran diferencia entre los perfiles de los alumnos en función de las decisiones tomadas en la PAU.
Esta situación ha sido estudiada en parte en trabajos previos (Nieto-Isidro, Martínez-Abad y Rodríguez-Conde, 2017Nieto-Isidro, S., Martínez-Abad, F. y Rodríguez-Conde, M. J. (2017). La influencia de la elección de materias en la Prueba de Acceso a la Universidad en los conocimientos matemáticos de los estudiantes de ingeniería. Revista Complutense de Educación 28(1), 125-144. doi: http://doi.org/10.5209/rev_RCED.2017.v28.n1.48977), analizando el nivel matemático de los estudiantes de nuevo ingreso en seis titulaciones de ingeniería desde 2010 hasta 2014, mostrando la presencia de grupos de estudiantes con conocimientos matemáticos dispares en función de sus decisiones sobre el examen de Matemáticas de la prueba de acceso. En este trabajo se pretende ir un paso más allá, relacionando dichos resultados con los de los estudiantes que se examinaron con la legislación de la etapa 1999-2009.
El principal problema de los estudios que abarcan periodos tan extensos (18 años) está en la disponibilidad de datos. Las Administraciones nacionales o regionales que se encargan de diseñar y corregir las pruebas no aportan datos individuales, sino agrupados, lo que dificulta el análisis de los conocimientos de los estudiantes. Tampoco se pueden conectar esos datos globales de los resultados en la prueba de acceso con la elección posterior de titulación universitaria de los estudiantes. Afortunadamente, este trabajo dispone de datos sobre las respuestas a un test de cálculo básico por más de 800 estudiantes que han accedido a 8 titulaciones de ingeniería en la Universidad de Salamanca (España) desde 1999. Estos datos presentan un gran interés, pues permiten dar una visión diacrónica del nivel de conocimientos matemáticos durante casi dos décadas y analizar si estos conocimientos matemáticos se han visto afectados por las normativas de acceso vigentes en cada periodo. Además, aunque los datos corresponden a una única universidad, la amplitud temporal y la diversidad de titulaciones pueden evitar la presencia de sesgos.
Estudios sobre matemáticas y acceso a la universidad en España y Europa
Existen diversos estudios empíricos sobre los contenidos de matemáticas de la PAU en España. Ya con la legislación del periodo 1999-2009, encontramos trabajos que analizan la influencia de la PAU en los conocimientos de matemáticas del Bachillerato, como los de Alsina (2001Alsina, C. (2001). Las Pruebas de Acceso a la Universidad (PAU) como brújula curricular. Aula de Innovación Educativa, 105, 66-70. ) y Zuazua y Rodríguez del Río (2002Zuazua E. y Rodríguez del Río, R. (2002). Enseñar y aprender matemáticas: del instituto a la universidad. Revista de Educación, 329, 239-256.). Los trabajos de Contreras, Ordóñez y Wilhelmi (2010Contreras, A., Ordóñez, L. y Wilhelmi, M. (2010). Influencia de las pruebas de acceso a la universidad en la enseñanza de la integral definida en el bachillerato. Enseñanza de las Ciencias, 28(3), 367-384. doi: http://doi.org/10.5565/rev/ec/v28n3.63 ) y Ordóñez y Contreras (2011Ordóñez, L. y Contreras, A. (2011). La integral definida en bachillerato: restricciones institucionales de las pruebas de acceso a la universidad. En M. Marín, G. Fernández, L. J. Blanco y M. Palarea (eds.), Investigación en Educación Matemática XV (pp. 461-470). Ciudad Real: Sociedad Española de Investigación en Educación Matemática. Recuperado de http://www.seiem.es/docs/actas/15/Actas15SEIEM.pdf) se centran en el caso de la influencia de la PAU sobre la docencia de la integral en el Bachillerato. Recientemente, Oliva, Franco y Gil (2018) han incidido en la repercusión de la PAU tanto en la metodología docente como en las prácticas evaluativas de los profesores de asignaturas de ciencias del Bachillerato.
En el caso de los estudiantes que acceden a titulaciones de ingeniería en el periodo 1999-2009, Boal, Bueno, Lerís y Sein-Echaluce (2008Boal, N., Bueno, C., Lerís, M. D. y Sein-Echaluce, M. L. (2008). Las habilidades matemáticas evaluadas en las pruebas de acceso a la universidad. Un estudio en varias universidades públicas españolas. Revista de Investigación Educativa, 26(1), 11-23.), con estudiantes de ingeniería técnica de la Universidad de Zaragoza, detectan un enfoque superficial del aprendizaje de las matemáticas en el Bachillerato destinado a reproducir la información solicitada en la PAU. Huidobro, Méndez y Serrano (2010Huidobro, J. A., Méndez, A. y Serrano, M. L. (2010). Del bachillerato a la universidad: las matemáticas en las carreras de ciencia y tecnología. Aula Abierta, 38(1), 71-80. doi: http://doi.org/10.17811/rifie.38.95.2010 ), con estudiantes de ingeniería de la Universidad de Oviedo, destacan la influencia de la PAU en el proceso de enseñanza-aprendizaje de los contenidos matemáticos en el Bachillerato. También Riaguas, Arribas, Celorrio y Lerís (2006Riaguas, A., Arribas, M., Celorrio, R. y Lerís, D. (2006). El acceso a los estudios de ingeniería: detección de debilidades o carencias formativas en matemáticas. Actas del 4.o Congreso Internacional de Docencia Universitaria e Innovación, CIDUI. ), con estudiantes de ingeniería e ingeniería técnica de la Universidad de Zaragoza, encuentran carencias en el manejo de los símbolos matemáticos, en el uso del lenguaje simbólico y gráfico y en la aplicación de las matemáticas a su entorno, señalando que los estudiantes han recibido una enseñanza dirigida a superar la prueba de Matemáticas de la PAU. En contraste con estos trabajos, Ruiz de Gauna, Dávila, Etxeberría y Sarasua (2013Ruiz de Gauna, J. y Sarasua, J. (2013). Estudio comparado de los resultados de las pruebas de acceso a la universidad en Cataluña, Comunidad Valenciana y País Vasco. Ikastorratza, e-Revista de Didáctica, 11, 1-24.), analizando los resultados de la prueba de Matemáticas II de la PAU desde 1994 a 2008 y las opiniones de los profesores en el curso 2009-2010, indican que el objetivo último del proceso de enseñanza-aprendizaje de las matemáticas desde el punto de vista de los profesores es que los alumnos aprendan, por encima de la preparación de la PAU.
Al producirse el cambio normativo en 2010, emergen algunos estudios sobre los resultados obtenidos en los exámenes de Matemáticas con la nueva Prueba de Acceso a la Universidad (PAU). El estudio de Ruiz de Gauna y Sarasua (2011Ruiz de Gauna, J. y Sarasua, J. (2011). ¿Mejoran los resultados con el nuevo sistema de selectividad? Bordón. Revista de Pedagogía, 63(4), 111-121. doi: http://doi.org/10.1016/j.aula.2015.01.002 ) analiza los resultados globales para la Universidad del País Vasco comparándolos con los de los cursos precedentes, mostrando cómo la nota media de la asignatura de Matemáticas permanece igual a la de las convocatorias anteriores, siendo ligeramente superior en los exámenes realizados en la fase general frente a la fase específica. Los mismos autores (Ruiz de Gauna y Sarasua, 2013Ruiz de Gauna, J. y Sarasua, J. (2013). Estudio comparado de los resultados de las pruebas de acceso a la universidad en Cataluña, Comunidad Valenciana y País Vasco. Ikastorratza, e-Revista de Didáctica, 11, 1-24.), analizando las notas obtenidas en diversas asignaturas en las comunidades autónomas de Cataluña, País Vasco y Comunidad Valenciana, evidencian que Matemáticas II es una asignatura típica de la fase general más que de la fase específica, al no estar ligada a unos estudios universitarios concretos.
En las titulaciones de ingeniería se observa que, frente a lo pretendido por la ley (potenciar los perfiles más adecuados para cada titulación), el sistema de acceso provoca que un porcentaje importante de los estudiantes no hayan superado el examen de Matemáticas de la PAU o no se hayan examinado de esta materia. Así, Heredia, Méndez y Moreno (2011Heredia, S., Méndez, D. y Moreno, J. (2011). Datos de acceso de los estudiantes del Grado en Ingeniería de la Edificación. IX Jornadas de Redes de Investigación en Docencia Universitaria: Diseño de Buenas Prácticas Docentes en el Contexto Actual. Alicante, España. ), analizando los resultados en las pruebas de Física, Matemáticas y Dibujo de la PAU de estudiantes de Ingeniería de la Edificación en la Universidad de Alicante, encuentran que, aun superando la PAU de forma global, un 62% de los estudiantes de la convocatoria de 2010 no superaron el examen de Matemáticas II, frente al 55% de suspensos registrados en las convocatorias de 2009 y anteriores. En Campo et al. (2016Campo, A., Álvarez, M. L., Beléndez, T., Heredia, S., Hernández, A., Moreno, J. C., Ortuño, M., Rosa, J. L., Torrejón, J. M. y Verdú, F. J. (2016). Destrezas matemáticas previas de los estudiantes de Grado en Ingenierías y Arquitectura (II). En R. Roig, J. E. Blasco, A. Lledó y N. Pellín, (eds.), Investigación e innovación educativa en docencia universitaria. Retos, propuestas y acciones. (pp. 2915-2934). Alicante: CEI Universidad de Alicante.), con alumnos de ingeniería y arquitectura de la Universidad de Oviedo, solo un 55% de los estudiantes de la muestra afirman haber aprobado el examen de Matemáticas de la PAU. Los datos analizados por Nieto-Isidro et al. (2017Nieto-Isidro, S., Martínez-Abad, F. y Rodríguez-Conde, M. J. (2017). La influencia de la elección de materias en la Prueba de Acceso a la Universidad en los conocimientos matemáticos de los estudiantes de ingeniería. Revista Complutense de Educación 28(1), 125-144. doi: http://doi.org/10.5209/rev_RCED.2017.v28.n1.48977) encuentran un grupo importante de alumnos de Bachillerato (casi un 32%) que han evitado la prueba de Matemáticas en la PAU, junto con otro porcentaje importante (cerca del 26%) de estudiantes de Bachillerato que no han superado dicho examen. En total, menos de la mitad de los alumnos de Bachillerato de la muestra (un 42%) han superado el examen de Matemáticas de la PAU.
Estos estudios, que inciden específicamente sobre el papel de la PAU, se unen a otros trabajos más generales sobre los conocimientos matemáticos de los estudiantes que acceden a titulaciones de ingeniería en España después de 2010. Así, Cobos, Arevalillo, Moreno y Olanda (2013Cobos, M., Arevalillo, M., Moreno, P. y Olanda, R. (2013). Estudiando el nivel en matemáticas de alumnos de nuevo ingreso en Ingeniería Informática: percepción y realidad. Actas de las XIX Jornadas sobre la Enseñanza Universitaria de la Informática (pp. 233-239). Castellón, España.), con una muestra de estudiantes de Informática de la Universidad de Valencia, analizan el rendimiento frente a un test de 8 preguntas en función de la procedencia (Bachillerato y Formación Profesional) y la valoración que poseen sobre sus conocimientos de matemáticas: según estos autores los estudiantes tienden a sobrevalorar su nivel matemático, considerándolo más alto de lo que es en realidad. Campo et al. (2016Campo, A., Álvarez, M. L., Beléndez, T., Heredia, S., Hernández, A., Moreno, J. C., Ortuño, M., Rosa, J. L., Torrejón, J. M. y Verdú, F. J. (2016). Destrezas matemáticas previas de los estudiantes de Grado en Ingenierías y Arquitectura (II). En R. Roig, J. E. Blasco, A. Lledó y N. Pellín, (eds.), Investigación e innovación educativa en docencia universitaria. Retos, propuestas y acciones. (pp. 2915-2934). Alicante: CEI Universidad de Alicante.) encuentran que apenas un 25% de los estudiantes de primer curso de ingeniería y de arquitectura de la Universidad de Oviedo pueden contestar con seguridad a cuestiones básicas sobre geometría. Un estudio más reciente de Castro et al. (2018Castro, M. A., García, P. A., Sirvent, A., Cabrera J., Bueno, A. M., Alustiza, M. y Rodríguez, F. (2018). Conocimientos previos de matemáticas del alumnado en titulaciones de Ingeniería: un análisis sincrónico y diacrónico. En R. Roig (ed.), El compromiso académico y social a través de la investigación e innovación educativas en la enseñanza superior (pp. 112-124). Barcelona: Ediciones Octaedro.) compara los resultados de un test sobre temas de álgebra cumplimentado por los estudiantes de ingeniería de diversas titulaciones de la Universidad de Alicante en los cursos académicos 2001-2002 y 2017-2018, encontrando que los conocimientos matemáticos son inferiores en los grupos del curso académico 2017-2018 frente a los del grupo de 2001-2002; en este estudio también se muestra que hay una relación positiva entre los resultados en el test de álgebra y la nota de la PAU.
En el contexto europeo, la SEFI (Sociedad Europea para la Educación de los Ingenieros) destaca la falta de homogeneidad de los conocimientos matemáticos de los estudiantes de nuevo ingreso en ingeniería, indicando que es un problema extendido en toda Europa (Alpers et al. 2013Alpers, B. A., Demlova, M., Fant, C. H., Gustafsson, T., Lawson, D., Olsson-Lehtonen, B., Robinson, C. y Velichova, D. (2013). A framework for mathematics curricula in Engineering Education. Bruselas: European Society for Engineering Education (SEFI). Recuperado de http://sefi.htw-aalen.de/Curriculum/Competency based curriculum incl ads.pdf). A nivel general, los estudios coinciden en señalar el bajo nivel de matemáticas en los estudiantes que inician estudios de ingeniería; este nivel está muchas veces asociado a decisiones tomadas por las autoridades académicas sobre el currículum de matemáticas de los pregraduados, o está influido por los efectos de las políticas gubernamentales o universitarias que pretenden aumentar el número de estudiantes en determinadas titulaciones. En esta línea, podemos mencionar estudios recientes en países como Irlanda (Treacy y Faulkner, 2015Treacy, P. y Faulkner, F. (2015). Trends in basic mathematical competencies of beginning undergraduates in Ireland, 2003-2013. International Journal of Mathematical Education in Science and Technology, 46(8), 1182-1196. doi: http://doi.org/10.1080/0020739X.2015.1050707; Treacy, Faulkner y Prendergast, 2016Treacy, P., Faulkner, F. y Prendergast, M. (2016). Analysing the correlation between secondary mathematics curriculum change and trends in beginning undergraduates’ performance of basic mathematical skills in Ireland. Irish Educational Studies, 35(4), 381-401. doi: http://doi.org/10.1080/03323315.2016.1243067 ), Reino Unido (Munns, 2017Munns, A. (2017). A study of competence in mathematics and mechanics in an engineering curriculum. European Journal of Engineering Education, 42(6), 1062-1075. doi: 10.1080/03043797.2016.1259292 ), Alemania (Derr, Hübl y Ahmed, 2018Derr, K., Hübl, R. y Ahmed, M. Z. (2018). Prior knowledge in mathematics and study success in engineering: informational value of learner data collected from a web-based pre-course. European Journal of Engineering Education, 43(6), 911-926. doi:10.1080/03043797.2018.1462765 ), Suecia (Bergsten, Jablonka y Ashjari, 2016Bergsten, C., Jablonka, E. y Ashjari, H. (2016). The transition from secondary to tertiary mathematics education—a Swedish study. En 13th International Congress on Mathematical Education. Hamburgo, Alemania.) o Noruega (Nortvedt y Siqveland, 2019Nortvedt, G. A. y Siqveland, A. (2019). Are beginning calculus and engineering students adequately prepared for higher education? An assessment of students’ basic mathematical knowledge. International Journal of Mathematical Education in Science and Technology, 50(3), 325-343.), así como algunos estudios comparativos en los que se analizan los sistemas escolares y el nivel matemático de los estudiantes que acceden a titulaciones de ingeniería en diversos países, como el de Carr et al. (2015Carr, M., Fidalgo, C., Bigotte de Almeida, M. E., Branco, J. R., Santos, V., Murphy, E. y Ní Fhloinn, E. (2015) Mathematics diagnostic testing in engineering: an international comparison between Ireland and Portugal. European Journal of Engineering Education, 40(5), 546-556. doi: http://doi.org/10.1080/03043797.2014.967182) entre Irlanda y Portugal, o el de Cole, McCartan, Tuoni y Steinby (2014Cole, J. S., McCartan, C. D., Tuohi, R. y Steinby, P. (2014). Mathematics background of engineering students in Northern Ireland and Finland. Proceedings of 10th International CDIO Conference. Barcelona, España. ) entre Irlanda y Finlandia.
Objetivos
A partir de este estado de la cuestión, tanto nacional como internacional, en este trabajo se analiza si los conocimientos matemáticos de los estudiantes que acceden a estudios de ingeniería han variado significativamente en los últimos 18 años. Así, se pretende realizar una evaluación diagnóstica de los conocimientos matemáticos de los estudiantes que inician diversos estudios de ingeniería en la Universidad de Salamanca, analizando los cambios a lo largo del tiempo en la variable criterio a partir de grupos que reúnen unas características comunes.
Se plantea un diseño no experimental evolutivo de retardo temporal (Ato, López y Benavente, 2013Ato, M., López, J. J. y Benavente, A. (2013). Un sistema de clasificación de los diseños de investigación en psicología. Anales de Psicología, 29(3), 1038-1059. doi: http://doi.org/10.6018/analesps.29.3.178511 ), estableciendo medidas transversales repetidas a lo largo de 18 cursos académicos, desde 1999 hasta 2017. Para ello se mide el cambio o evolución a lo largo del tiempo de grupos de sujetos distintos, pero analizados en el mismo momento de su vida académica, que cumplen unas condiciones determinadas en el fenómeno estudiado, sin llevar a cabo ningún tipo de manipulación de las variables ni aplicar tratamiento alguno. Además, se considerarán dos etapas legislativas diferentes: la etapa 1 (1999-2000 hasta 2008-2009) y la etapa 2 (2011-2012 hasta 2016-2017), y dentro de la segunda etapa se establecerá una división entre los sujetos en función de sus resultados en la prueba de Matemáticas II de la PAU.
Población y muestra
Se parte de una población de estudiantes de nuevo acceso a titulaciones de ingeniería en la Universidad de Salamanca (España). De los 826 cuestionarios de cálculo básico cumplimentados desde 1999 a 2017, se realiza un primer filtrado eliminando los estudiantes procedentes de la Formación Profesional, los estudiantes repetidores y los cuestionarios con datos incompletos. Se obtiene así una muestra final de 627 estudiantes procedentes de Bachillerato, que ingresaron en el periodo 1999-2017 en un total de 8 titulaciones de ingeniería (Obras Públicas, Topografía, Arquitectura Técnica, Informática, Ingeniería Civil, Ingeniería Mecánica, Ingeniería de Materiales e Ingeniería Agroalimentaria). Estas titulaciones han ido variando a lo largo del periodo en función del encargo docente, la entrada de nuevas titulaciones y la implantación del EEES, con un mínimo de 2 y un máximo de 6 titulaciones en cada año.
Dado que el tamaño de la muestra recogida durante alguno de los cursos fue muy reducido (debido principalmente a la baja matrícula alcanzada en algunos cursos durante la primera etapa y a la variación en el número de titulaciones analizadas a lo largo del periodo), para obtener estimaciones más estables de las proporciones y promedios muestrales, los datos se agruparon en bienios, considerando cinco bienios en la etapa 1 (1999-2001, 2001-2003, 2003-2005, 2005-2007 y 2007-2009) y tres bienios en la etapa 2 (2011-2013, 2013-2015 y 2015-2017). Se dispone de 205 estudiantes en la etapa 1 (32,7%), 287 estudiantes en la etapa 2 que realizaron el examen de Matemáticas en la PAU (45,8%) y 135 estudiantes que accedieron por la PAU sin examinarse en Matemáticas o sin superar dicho examen (21,5%). La distribución de estudiantes para cada bienio, así como la etiqueta empleada en el estudio, se presentan en la tabla 1.
| Tabla 1. Distribución de la muestra por bienios | |||||||||||||||||||||||||||
|
Instrumento
Para el estudio se seleccionaron los ítems de los bloques de contenido exponencial y logaritmo y derivación e integración (7 ítems) de una escala validada a nivel de contenido y psicométrico, mediante aplicación de modelos de teoría de respuesta al ítem de un parámetro, para medir conocimientos básicos de cálculo (Nieto-Isidro et al., 2017Nieto-Isidro, S., Martínez-Abad, F. y Rodríguez-Conde, M. J. (2017). La influencia de la elección de materias en la Prueba de Acceso a la Universidad en los conocimientos matemáticos de los estudiantes de ingeniería. Revista Complutense de Educación 28(1), 125-144. doi: http://doi.org/10.5209/rev_RCED.2017.v28.n1.48977). La selección de estos 7 ítems sobre el total del instrumento inicial respondió a su inclusión en el core zero (Alpers et al. 2013Alpers, B. A., Demlova, M., Fant, C. H., Gustafsson, T., Lawson, D., Olsson-Lehtonen, B., Robinson, C. y Velichova, D. (2013). A framework for mathematics curricula in Engineering Education. Bruselas: European Society for Engineering Education (SEFI). Recuperado de http://sefi.htw-aalen.de/Curriculum/Competency based curriculum incl ads.pdf; Mustoe y Lawson, 2002Mustoe, L. y Lawson, D. (2002). A curriculum for the twenty-first century. Recuperado de http://sefi.htw-aalen.de/Curriculum/sefimarch2002.pdf ) propuesto por la SEFI (Sociedad Europea para la Educación de los Ingenieros): se trata de conocimientos básicos de matemáticas que deben poseer los estudiantes para abordar con éxito los estudios de ingeniería. Se trata además de ítems que han permanecido inalterados tanto en los currículos de Bachillerato como en los test cumplimentados por los estudiantes a lo largo de todo el periodo de estudio. Los 7 ítems seleccionados están recogidos en la tabla 2, junto con la etiqueta utilizada por cada ítem en el trabajo, el ámbito de estudio al que pertenecen y la redacción de cada cuestión.
| Tabla 2. Ítems medidos en el estudio | ||||||||||||||||||||||||
|
Al tratarse de ítems dicotómicos, se comprobó la dimensionalidad del instrumento a partir de un análisis factorial exploratorio basado en la matriz de correlaciones tetracóricas. La extracción de dos dimensiones dio lugar a una estructura factorial ajustada al modelo teórico, que absorbió el 52,42% de la varianza. El coeficiente alfa de Cronbach ordinal fue de .711 para la dimensión exponencial-logaritmo y de .674 para la dimensión derivación-integración.
Estos ítems permiten estudiar los conocimientos sobre la exponencial, el logaritmo neperiano, la relación entre ambos y sus representaciones gráficas, así como las habilidades para la derivación y la integración en algunos casos particulares. La escala de medición de estos ítems es de naturaleza dicotómica, valorando si el estudiante es capaz de responder correctamente a la cuestión planteada. En los ítems etiquetados como “teóricos” (T_1, T_2, T_3 y T_4), se debe responder verdadero/falso a una serie de afirmaciones; mientras que en los ítems etiquetados como “prácticos” (P_1, P_2 y P_3), se debe desarrollar en el papel un pequeño problema (dibujar aproximadamente una función, resolver una integral) que se valora como correctamente o incorrectamente resuelto. En el caso de las gráficas, se valora como positiva una representación aproximada que muestre las principales características de las funciones, y en el caso de la integración, la identificación de la integración por partes y la aplicación de este procedimiento.
Se contemplaron como variables criterio del estudio los aciertos registrados en los 7 ítems evaluados, y como variables predictoras tanto el tiempo (los bienios y/o la etapa legislativa) como la pertenencia a los distintos grupos de estudiantes analizados (en función de la etapa legislativa y/o la superación del examen de Matemáticas de la PAU en la segunda etapa a partir de la información proporcionada por los estudiantes al cumplimentar el test).
Procedimiento de recogida y análisis de datos
Inicialmente, se llevó a cabo un estudio descriptivo de la proporción de respuestas correctas en los 7 ítems a lo largo de los bienios y en función de los 3 grupos definidos (primera etapa y segunda etapa con y sin Matemáticas).
Se parte de la hipótesis de que tanto el cambio del marco legal de la PAU como la elección de las Matemáticas por parte del estudiante en este examen tienen efectos significativos sobre el nivel de conocimientos matemáticos (exponencial-logaritmo y derivación-integración) iniciales de los estudiantes universitarios de ingenierías. Así, se lleva a cabo un estudio inferencial para comparar los conocimientos de los 3 grupos definidos (con un 95% de confianza). Las comparaciones post hoc por parejas se acompañaron del cálculo del tamaño del efecto a través del estadístico d (Cohen, 1969Cohen, J. (1969). Statistical power analysis for the behavioral sciences. Nueva York: Academic Press.).
La tabla 3 muestra el porcentaje de aciertos en cada uno de los ítems para cada bienio y para la muestra completa de estudiantes. En la muestra completa (primera fila), solo hay dos cuestiones con porcentaje de acierto superior al 50%, la T_1 (relación entre el logaritmo y la exponencial, contestada correctamente por el 80,06% de los estudiantes) y la T_3 (determinar si la derivada de una función polinómica se anula en un punto, contestada correctamente por el 52,31% de los estudiantes). En el otro extremo, el ítem P_3 sobre la aplicación de la técnica de integración por partes solo es respondido correctamente por el 12,60% del grupo total.
| Tabla 3. Porcentaje de acierto de los ítems según el bienio y para todos los alumnos | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Considerando los diferentes bienios, en los ítems sobre cálculo exponencial y logarítmico (T_1, T_2, P_1 y P_2), los estudiantes de los bienios correspondientes a la etapa 2 obtienen siempre promedios de aciertos más altos que los estudiantes de los bienios correspondientes a la etapa 1. En los ítems sobre derivación e integración (T_3, T_4 y P_3), estas diferencias son menos perceptibles, decantándose en ocasiones por los estudiantes de la etapa 1. Los estudiantes de la etapa 1 en la muestra parecen dominar mejor la aplicación de la técnica de integración por partes (ítem P_3) que los de la etapa 2.
En la tabla 4 se agrupan los sujetos por etapas, mostrando los resultados para todos los estudiantes de la etapa 1 (E1-99-09) frente a todos los estudiantes de la etapa 2 (E2-11-17). Se observa que entre los estudiantes de la muestra existen diferencias según la etapa: en los ítems T_1, T_2, P_1 y P_2 (exponencial y logaritmo) y T_3 (derivación) estas diferencias van a favor de los estudiantes de la etapa 2, mientras que en los ítems T_4 y P_3 (integración), los mejores resultados corresponden a los estudiantes de la etapa 1.
| Tabla 4. Porcentaje de aciertos en los ítems según la etapa | ||||||||||||||||||||||||
|
En un segundo paso, se refina el análisis anterior separando a los estudiantes de la etapa 2 (2011-2017) en dos grupos: por una parte, los que superaron el examen de Matemáticas II en la PAU (E2-11-17-SÍ) frente a los que no lo superaron o no realizaron el examen (E2-11-17-NO): los resultados se muestran en la tabla 5.
| Tabla 5. Porcentaje de aciertos en los ítems según la etapa y la superación del examen de Matemáticas de la PAU | ||||||||||||||||||||||||||||||||
|
La tabla 5 muestra una tendencia sistemática en el porcentaje de aciertos, que siempre es favorable a los estudiantes del grupo E2-11-17-SÍ frente a los demás grupos. Aún así, estos estudiantes presentan aciertos superiores al 50% en solamente cuatro de los siete ítems considerados (T_1, T_2, P_1 y T_3).
Los estudiantes del grupo E2-11-17-NO presentan un nivel siempre inferior que el grupo E2-11-17-SÍ; comparándolos con el grupo E1-99-09 los resultados dependen del contenido matemático analizado, mostrando mejores resultados en los ítems sobre logaritmos y exponenciales (T_1, T_2, P_1 y P_2), resultados comparables en derivación (T_3) y peores resultados en integración (T_4 y P_3). Estos grupos de estudiantes solo presentan aciertos superiores al 50% en el ítem T_1.
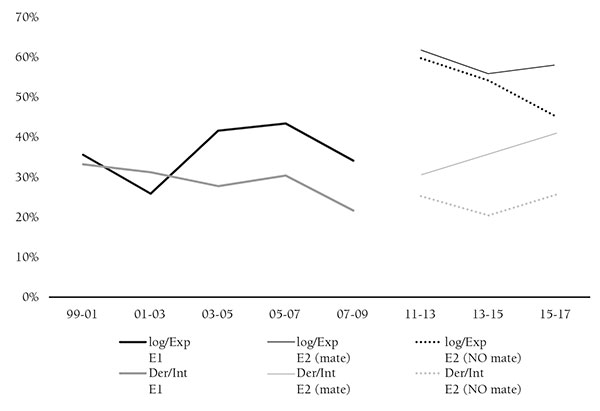
Al agrupar los ítems por ámbitos de conocimiento en términos promedio se pueden observar mejor estas tendencias. La figura 1 representa los porcentajes de acierto de los estudiantes de la etapa 1 y los estudiantes de la etapa 2 que realizaron y no realizaron el examen de Matemáticas de la PAU a lo largo del periodo estudiado para los dos ámbitos de conocimiento analizados (logaritmos/exponenciales y derivadas/integrales).
En la figura 1 quedan patentes los mejores resultados globales sobre logaritmos y exponenciales frente a la derivación e integración, que tienen menores porcentajes de acierto. En el caso de las exponenciales y los logaritmos, se observa un mejor comportamiento de los estudiantes de la muestra en la etapa 2, especialmente en el grupo E2-11-17-SÍ frente al grupo E2-11-17-NO. Para las derivadas e integrales, hay una mayor estabilidad en la respuesta excepto en el grupo E2-11-17-NO, que presenta un comportamiento claramente inferior al de los demás grupos.
|
Figura 1. Desempeño global de los grupos considerados según el ámbito de los ítems 
|
El análisis inferencial de las diferencias obtenidas entre los grupos se muestra en la tabla 6. La aplicación del ANOVA (con el cálculo de la prueba post hoc T3 de Dunnet debido a la heterocedasticidad de los grupos) muestra diferencias significativas en ambas dimensiones evaluadas. Las pruebas post hoc confirman las observaciones previas: los estudiantes de la etapa 1 obtienen puntuaciones más bajas en exponenciales y logaritmos (con un tamaño del efecto sensiblemente superior en la comparación con el grupo E2-11-17-SÍ) y los estudiantes del grupo E2-11-17-NO alcanzan rendimientos inferiores en derivación e integración, aunque con tamaños del efecto de moderados a bajos. Por su parte, los estudiantes del grupo E2-11-17-SÍ presentan puntuaciones superiores en todos los casos, alcanzando en las comparaciones con el grupo E2-11-17-NO tamaños del efecto medios-bajos.
| Tabla 6. Análisis inferencial de las diferencias entre los grupos considerados | |||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
La importancia de las políticas educativas y su influencia en los niveles de conocimientos matemáticos de los estudiantes al ingresar en la universidad está bien documentada en diversos países europeos, en particular para los estudios técnicos y de ingeniería, en los que las matemáticas tienen una importancia primordial. En el caso de España, la PAU influye tanto en los contenidos cursados en Bachillerato como en la forma de adquirirlos, impartirlos o evaluarlos (Alsina, 2001Alsina, C. (2001). Las Pruebas de Acceso a la Universidad (PAU) como brújula curricular. Aula de Innovación Educativa, 105, 66-70. ; Boal et al., 2008Boal, N., Bueno, C., Lerís, M. D. y Sein-Echaluce, M. L. (2008). Las habilidades matemáticas evaluadas en las pruebas de acceso a la universidad. Un estudio en varias universidades públicas españolas. Revista de Investigación Educativa, 26(1), 11-23.; Contreras et al., 2010Contreras, A., Ordóñez, L. y Wilhelmi, M. (2010). Influencia de las pruebas de acceso a la universidad en la enseñanza de la integral definida en el bachillerato. Enseñanza de las Ciencias, 28(3), 367-384. doi: http://doi.org/10.5565/rev/ec/v28n3.63 ; Ordóñez y Contreras, 2011Ordóñez, L. y Contreras, A. (2011). La integral definida en bachillerato: restricciones institucionales de las pruebas de acceso a la universidad. En M. Marín, G. Fernández, L. J. Blanco y M. Palarea (eds.), Investigación en Educación Matemática XV (pp. 461-470). Ciudad Real: Sociedad Española de Investigación en Educación Matemática. Recuperado de http://www.seiem.es/docs/actas/15/Actas15SEIEM.pdf; Oliva et al., 2018Oliva, J. M., Franco, R. y Gil, M. L. (2018). Influencia de las pruebas de acceso a la universidad en la metodología docente del profesorado de ciencias. Ápice. Revista de Educación Científica, 2(1), 1-17. doi: http://doi.org/10.17979/arec.2018.2.1.3197 ; Zuazua y Rodríguez del Río, 2002Zuazua E. y Rodríguez del Río, R. (2002). Enseñar y aprender matemáticas: del instituto a la universidad. Revista de Educación, 329, 239-256.). Así, un cambio legislativo que afecte a la PAU afectará también a los conocimientos de los estudiantes cuando inician sus carreras universitarias.
Este trabajo analiza esta influencia sobre algunos ítems matemáticos básicos de cálculo, considerando estudiantes que iniciaron diversos estudios de ingeniería en la Universidad de Salamanca durante 18 cursos académicos (1999-2000 hasta 2016-2017), con dos legislaciones educativas diferentes. Aunque hay estudios sobre el acceso a la universidad que incluyen varios años de estudio (Ruiz de Gauna et al., 2013Ruiz de Gauna J., Dávila, P., Extebarría, J. y Sarasua, J. (2013). Pruebas de selectividad en matemáticas en la UPV-EHU. Resultados y opiniones de los profesores. Revista de Educación, 362, 217-246.), o que analizan los resultados antes y/o después del cambio normativo (Castro et al., 2018Castro, M. A., García, P. A., Sirvent, A., Cabrera J., Bueno, A. M., Alustiza, M. y Rodríguez, F. (2018). Conocimientos previos de matemáticas del alumnado en titulaciones de Ingeniería: un análisis sincrónico y diacrónico. En R. Roig (ed.), El compromiso académico y social a través de la investigación e innovación educativas en la enseñanza superior (pp. 112-124). Barcelona: Ediciones Octaedro., Heredia et al., 2011Heredia, S., Méndez, D. y Moreno, J. (2011). Datos de acceso de los estudiantes del Grado en Ingeniería de la Edificación. IX Jornadas de Redes de Investigación en Docencia Universitaria: Diseño de Buenas Prácticas Docentes en el Contexto Actual. Alicante, España. ; Ruiz de Gauna y Sarasua 2011Ruiz de Gauna, J. y Sarasua, J. (2011). ¿Mejoran los resultados con el nuevo sistema de selectividad? Bordón. Revista de Pedagogía, 63(4), 111-121. doi: http://doi.org/10.1016/j.aula.2015.01.002 , 2013Ruiz de Gauna, J. y Sarasua, J. (2013). Estudio comparado de los resultados de las pruebas de acceso a la universidad en Cataluña, Comunidad Valenciana y País Vasco. Ikastorratza, e-Revista de Didáctica, 11, 1-24.), es difícil encontrar datos que tengan un recorrido tan amplio. Tampoco es habitual disponer de datos no agregados o que conecten los conocimientos al iniciar la universidad con el método de acceso utilizado por los alumnos, lo que dificulta la realización de estudios a gran escala y que superen el ámbito local.
Los resultados generales sobre conocimientos básicos de cálculo de los estudiantes de la muestra están en consonancia con otros estudios sobre el bajo nivel de conocimientos matemáticos de los estudiantes de nuevo ingreso en ingeniería en España, a lo largo de todos los años del estudio (Boal et al., 2008Boal, N., Bueno, C., Lerís, M. D. y Sein-Echaluce, M. L. (2008). Las habilidades matemáticas evaluadas en las pruebas de acceso a la universidad. Un estudio en varias universidades públicas españolas. Revista de Investigación Educativa, 26(1), 11-23.; Campo et al., 2016Campo, A., Álvarez, M. L., Beléndez, T., Heredia, S., Hernández, A., Moreno, J. C., Ortuño, M., Rosa, J. L., Torrejón, J. M. y Verdú, F. J. (2016). Destrezas matemáticas previas de los estudiantes de Grado en Ingenierías y Arquitectura (II). En R. Roig, J. E. Blasco, A. Lledó y N. Pellín, (eds.), Investigación e innovación educativa en docencia universitaria. Retos, propuestas y acciones. (pp. 2915-2934). Alicante: CEI Universidad de Alicante.; Castro et al., 2018Castro, M. A., García, P. A., Sirvent, A., Cabrera J., Bueno, A. M., Alustiza, M. y Rodríguez, F. (2018). Conocimientos previos de matemáticas del alumnado en titulaciones de Ingeniería: un análisis sincrónico y diacrónico. En R. Roig (ed.), El compromiso académico y social a través de la investigación e innovación educativas en la enseñanza superior (pp. 112-124). Barcelona: Ediciones Octaedro.; Cobos et al., 2013Cobos, M., Arevalillo, M., Moreno, P. y Olanda, R. (2013). Estudiando el nivel en matemáticas de alumnos de nuevo ingreso en Ingeniería Informática: percepción y realidad. Actas de las XIX Jornadas sobre la Enseñanza Universitaria de la Informática (pp. 233-239). Castellón, España.; Heredia et al., 2011Heredia, S., Méndez, D. y Moreno, J. (2011). Datos de acceso de los estudiantes del Grado en Ingeniería de la Edificación. IX Jornadas de Redes de Investigación en Docencia Universitaria: Diseño de Buenas Prácticas Docentes en el Contexto Actual. Alicante, España. ; Nieto-Isidro et al., 2017Nieto-Isidro, S., Martínez-Abad, F. y Rodríguez-Conde, M. J. (2017). La influencia de la elección de materias en la Prueba de Acceso a la Universidad en los conocimientos matemáticos de los estudiantes de ingeniería. Revista Complutense de Educación 28(1), 125-144. doi: http://doi.org/10.5209/rev_RCED.2017.v28.n1.48977; Riaguas et al., 2006Riaguas, A., Arribas, M., Celorrio, R. y Lerís, D. (2006). El acceso a los estudios de ingeniería: detección de debilidades o carencias formativas en matemáticas. Actas del 4.o Congreso Internacional de Docencia Universitaria e Innovación, CIDUI. ). Incluso los estudiantes de la muestra que tienen un mejor desempeño en la prueba presentan un porcentaje de aciertos inferior al 50% en tres de los siete ítems del estudio, especialmente los prácticos, donde los resultados son especialmente bajos en los ítems referidos a las técnicas de integración. Los estudiantes de la muestra con peor desempeño en la prueba presentan un porcentaje de acierto superior al 50% en un único ítem. Esta situación es relevante, puesto que el nivel de conocimientos matemáticos al comenzar los estudios de ingeniería es uno de los mejores predictores del éxito académico o del abandono temprano de estos estudiantes (Darlington y Bowyer, 2017Darlington, E., y Bowyer, J. (2017). Engineering undergraduates’ views of A-level Mathematics and Further Mathematics as preparation for their degree. Teaching Mathematics and its Applications, 36(4), 200-216. doi: http://doi.org/10.1093/teamat/hrw020 ; Faulkner, Hannigan y Fitzmaurice, 2014Faulkner, F., Hannigan, A. y Fitzmaurice, O. (2014). The role of prior mathematical experience in predicting mathematics performance in higher education. International Journal of Mathematical Education in Science and Technology, 45(5), 648-667. doi: http://doi.org/10.1080/0020739X.2013.868539).
En la muestra estudiada, hay un cambio estadísticamente significativo en el porcentaje de aciertos de los estudiantes en los ítems de cálculo básico, a lo largo de los 18 años incluidos en el estudio. Ese cambio, que coincide con la introducción de la legislación sobre acceso a la universidad en 2010, se manifiesta especialmente al considerar en la segunda etapa dos grupos relacionados con su rendimiento ante el examen de Matemáticas de la PAU: los estudiantes que aprobaron dicho examen tienen mejor rendimiento en todos los ítems y para todo el periodo estudiado, tanto frente a los estudiantes de la primera etapa como frente a los estudiantes de la segunda etapa que no superaron o no se examinaron de Matemáticas. Este resultado contrasta con los obtenidos por Ruiz de Gauna et al. (2013Ruiz de Gauna J., Dávila, P., Extebarría, J. y Sarasua, J. (2013). Pruebas de selectividad en matemáticas en la UPV-EHU. Resultados y opiniones de los profesores. Revista de Educación, 362, 217-246.) y Heredia et al. (2011Heredia, S., Méndez, D. y Moreno, J. (2011). Datos de acceso de los estudiantes del Grado en Ingeniería de la Edificación. IX Jornadas de Redes de Investigación en Docencia Universitaria: Diseño de Buenas Prácticas Docentes en el Contexto Actual. Alicante, España. ), donde el cambio de legislación de acceso en 2010 afectó a las notas de Matemáticas II, que fueron más bajas al menos durante los primeros años. Una posible explicación a esta discrepancia es que en el presente estudio no analizamos directamente las notas obtenidas en el examen de Matemáticas de la PAU (que pueden haber sido más bajas en este periodo), sino los conocimientos matemáticos de los alumnos, modulados por la superación o no de dicho examen. Castro et al. (2018Castro, M. A., García, P. A., Sirvent, A., Cabrera J., Bueno, A. M., Alustiza, M. y Rodríguez, F. (2018). Conocimientos previos de matemáticas del alumnado en titulaciones de Ingeniería: un análisis sincrónico y diacrónico. En R. Roig (ed.), El compromiso académico y social a través de la investigación e innovación educativas en la enseñanza superior (pp. 112-124). Barcelona: Ediciones Octaedro.), cuando analizan la nota de Matemáticas en la PAU, muestran que correlaciona positivamente con el número de aciertos en el cuestionario de álgebra utilizado.
Un aspecto sorprendente es la presencia en las titulaciones de ingeniería del periodo 2010-2017 de estudiantes que no han realizado o no han superado el examen de Matemáticas en la PAU. Por una parte, es bien conocido que las matemáticas son básicas para la formación de los ingenieros (Alpers et al. 2013Alpers, B. A., Demlova, M., Fant, C. H., Gustafsson, T., Lawson, D., Olsson-Lehtonen, B., Robinson, C. y Velichova, D. (2013). A framework for mathematics curricula in Engineering Education. Bruselas: European Society for Engineering Education (SEFI). Recuperado de http://sefi.htw-aalen.de/Curriculum/Competency based curriculum incl ads.pdf; Faulkner et al., 2014Faulkner, F., Hannigan, A. y Fitzmaurice, O. (2014). The role of prior mathematical experience in predicting mathematics performance in higher education. International Journal of Mathematical Education in Science and Technology, 45(5), 648-667. doi: http://doi.org/10.1080/0020739X.2013.868539; Mustoe y Lawson, 2002Mustoe, L. y Lawson, D. (2002). A curriculum for the twenty-first century. Recuperado de http://sefi.htw-aalen.de/Curriculum/sefimarch2002.pdf ); por otra parte, los centros que imparten titulaciones de ingeniería ponderan positivamente la nota del examen de Matemáticas de los alumnos de nuevo ingreso, favoreciendo la entrada de los alumnos que tienen mejores resultados. En esta situación, sería esperable que los estudiantes que optan a estudios de ingeniería intentasen obtener la mayor nota posible en el examen de Matemáticas de la PAU para mejorar tanto su nota de acceso como sus conocimientos de la materia, pero no ocurre así en un porcentaje relevante.
Esta aparente contradicción, también detectada en otros estudios como el de Heredia et al. (2011Heredia, S., Méndez, D. y Moreno, J. (2011). Datos de acceso de los estudiantes del Grado en Ingeniería de la Edificación. IX Jornadas de Redes de Investigación en Docencia Universitaria: Diseño de Buenas Prácticas Docentes en el Contexto Actual. Alicante, España. ), Campo et al. (2016Campo, A., Álvarez, M. L., Beléndez, T., Heredia, S., Hernández, A., Moreno, J. C., Ortuño, M., Rosa, J. L., Torrejón, J. M. y Verdú, F. J. (2016). Destrezas matemáticas previas de los estudiantes de Grado en Ingenierías y Arquitectura (II). En R. Roig, J. E. Blasco, A. Lledó y N. Pellín, (eds.), Investigación e innovación educativa en docencia universitaria. Retos, propuestas y acciones. (pp. 2915-2934). Alicante: CEI Universidad de Alicante.) y Nieto-Isidro et al. (2017Nieto-Isidro, S., Martínez-Abad, F. y Rodríguez-Conde, M. J. (2017). La influencia de la elección de materias en la Prueba de Acceso a la Universidad en los conocimientos matemáticos de los estudiantes de ingeniería. Revista Complutense de Educación 28(1), 125-144. doi: http://doi.org/10.5209/rev_RCED.2017.v28.n1.48977), puede deberse a una “estrategia” por parte de los estudiantes que se presentan a la PAU, en la que consideran más importante aprobar la prueba de forma general que obtener una nota concreta en una asignatura. Las Matemáticas se suelen considerar una asignatura con un elevado nivel de dificultad, y como el sistema de acceso de la etapa 2010-2017 permitía un alto grado de decisión por parte de los estudiantes, es posible que los estudiantes prefiriesen examinarse de otras materias antes de “arriesgarse” con un examen más difícil. La posible penalización en la nota de acceso pierde relevancia dado que una gran parte de las titulaciones de ingeniería no requieren actualmente notas elevadas de acceso.
Estudios como el presente pueden aportar evidencias sobre la consecución de los objetivos previstos por las normativas de acceso a la universidad que dan un amplio margen de elección a los alumnos. Este tipo de normativas están dirigidas a dar mayor flexibilidad a los currículos de los alumnos de nuevo ingreso, mejorar los perfiles de acceso haciéndolos más específicos o ponderar positivamente las asignaturas más relacionadas con una determinada titulación. Sin embargo, a tenor de los resultados de este y otros estudios, se pueden generar situaciones no deseadas ni previstas por la legislación; una de ellas es la presencia en las aulas de las titulaciones de ingeniería de un nutrido grupo de estudiantes que presentan un bajo rendimiento en matemáticas al no haber realizado o superado el examen de Matemáticas de la PAU. Desde el punto de vista de la docencia de matemáticas, y aunque no son objeto de estudio en este trabajo, hay que añadir la incorporación de los estudiantes procedentes de ciclos profesionales debido a la eliminación del “cupo de entrada” en la legislación de 2010, y que constituyen un 26% en Heredia et al. (2011Heredia, S., Méndez, D. y Moreno, J. (2011). Datos de acceso de los estudiantes del Grado en Ingeniería de la Edificación. IX Jornadas de Redes de Investigación en Docencia Universitaria: Diseño de Buenas Prácticas Docentes en el Contexto Actual. Alicante, España. ), un 27% en Nieto-Isidro et al. (2017Nieto-Isidro, S., Martínez-Abad, F. y Rodríguez-Conde, M. J. (2017). La influencia de la elección de materias en la Prueba de Acceso a la Universidad en los conocimientos matemáticos de los estudiantes de ingeniería. Revista Complutense de Educación 28(1), 125-144. doi: http://doi.org/10.5209/rev_RCED.2017.v28.n1.48977) y hasta un 46% en Cobos et al. (2013Cobos, M., Arevalillo, M., Moreno, P. y Olanda, R. (2013). Estudiando el nivel en matemáticas de alumnos de nuevo ingreso en Ingeniería Informática: percepción y realidad. Actas de las XIX Jornadas sobre la Enseñanza Universitaria de la Informática (pp. 233-239). Castellón, España.).
La principal limitación de este estudio es su referencia a una única universidad dentro de una comunidad autónoma concreta, con estudiantes que acceden a titulaciones de ingeniería que no presentan notas de acceso elevadas. Sería muy interesante realizar un diagnóstico similar en otras comunidades autónomas, si fuera posible disponer de datos de tanto recorrido temporal. Asimismo, sería deseable poder comparar los resultados obtenidos en los ítems analizados por estudiantes de otras ingenierías que requieran notas de acceso más elevadas, o incluso por estudiantes que accediesen a otras titulaciones de ciencias en las que los conocimientos matemáticos básicos resulten también relevantes.
| ○ | Alpers, B. A., Demlova, M., Fant, C. H., Gustafsson, T., Lawson, D., Olsson-Lehtonen, B., Robinson, C. y Velichova, D. (2013). A framework for mathematics curricula in Engineering Education. Bruselas: European Society for Engineering Education (SEFI). Recuperado de http://sefi.htw-aalen.de/Curriculum/Competency based curriculum incl ads.pdf |
| ○ | Alsina, C. (2001). Las Pruebas de Acceso a la Universidad (PAU) como brújula curricular. Aula de Innovación Educativa, 105, 66-70. |
| ○ | Ato, M., López, J. J. y Benavente, A. (2013). Un sistema de clasificación de los diseños de investigación en psicología. Anales de Psicología, 29(3), 1038-1059. doi: http://doi.org/10.6018/analesps.29.3.178511 |
| ○ | Bergsten, C., Jablonka, E. y Ashjari, H. (2016). The transition from secondary to tertiary mathematics education—a Swedish study. En 13th International Congress on Mathematical Education. Hamburgo, Alemania. |
| ○ | Boal, N., Bueno, C., Lerís, M. D. y Sein-Echaluce, M. L. (2008). Las habilidades matemáticas evaluadas en las pruebas de acceso a la universidad. Un estudio en varias universidades públicas españolas. Revista de Investigación Educativa, 26(1), 11-23. |
| ○ | Campo, A., Álvarez, M. L., Beléndez, T., Heredia, S., Hernández, A., Moreno, J. C., Ortuño, M., Rosa, J. L., Torrejón, J. M. y Verdú, F. J. (2016). Destrezas matemáticas previas de los estudiantes de Grado en Ingenierías y Arquitectura (II). En R. Roig, J. E. Blasco, A. Lledó y N. Pellín, (eds.), Investigación e innovación educativa en docencia universitaria. Retos, propuestas y acciones. (pp. 2915-2934). Alicante: CEI Universidad de Alicante. |
| ○ | Carr, M., Fidalgo, C., Bigotte de Almeida, M. E., Branco, J. R., Santos, V., Murphy, E. y Ní Fhloinn, E. (2015) Mathematics diagnostic testing in engineering: an international comparison between Ireland and Portugal. European Journal of Engineering Education, 40(5), 546-556. doi: http://doi.org/10.1080/03043797.2014.967182 |
| ○ | Castro, M. A., García, P. A., Sirvent, A., Cabrera J., Bueno, A. M., Alustiza, M. y Rodríguez, F. (2018). Conocimientos previos de matemáticas del alumnado en titulaciones de Ingeniería: un análisis sincrónico y diacrónico. En R. Roig (ed.), El compromiso académico y social a través de la investigación e innovación educativas en la enseñanza superior (pp. 112-124). Barcelona: Ediciones Octaedro. |
| ○ | Cobos, M., Arevalillo, M., Moreno, P. y Olanda, R. (2013). Estudiando el nivel en matemáticas de alumnos de nuevo ingreso en Ingeniería Informática: percepción y realidad. Actas de las XIX Jornadas sobre la Enseñanza Universitaria de la Informática (pp. 233-239). Castellón, España. |
| ○ | Cohen, J. (1969). Statistical power analysis for the behavioral sciences. Nueva York: Academic Press. |
| ○ | Cole, J. S., McCartan, C. D., Tuohi, R. y Steinby, P. (2014). Mathematics background of engineering students in Northern Ireland and Finland. Proceedings of 10th International CDIO Conference. Barcelona, España. |
| ○ | Contreras, A., Ordóñez, L. y Wilhelmi, M. (2010). Influencia de las pruebas de acceso a la universidad en la enseñanza de la integral definida en el bachillerato. Enseñanza de las Ciencias, 28(3), 367-384. doi: http://doi.org/10.5565/rev/ec/v28n3.63 |
| ○ | Darlington, E., y Bowyer, J. (2017). Engineering undergraduates’ views of A-level Mathematics and Further Mathematics as preparation for their degree. Teaching Mathematics and its Applications, 36(4), 200-216. doi: http://doi.org/10.1093/teamat/hrw020 |
| ○ | Derr, K., Hübl, R. y Ahmed, M. Z. (2018). Prior knowledge in mathematics and study success in engineering: informational value of learner data collected from a web-based pre-course. European Journal of Engineering Education, 43(6), 911-926. doi: 10.1080/03043797.2018.1462765 |
| ○ | Faulkner, F., Hannigan, A. y Fitzmaurice, O. (2014). The role of prior mathematical experience in predicting mathematics performance in higher education. International Journal of Mathematical Education in Science and Technology, 45(5), 648-667. doi: http://doi.org/10.1080/0020739X.2013.868539 |
| ○ | Heredia, S., Méndez, D. y Moreno, J. (2011). Datos de acceso de los estudiantes del Grado en Ingeniería de la Edificación. IX Jornadas de Redes de Investigación en Docencia Universitaria: Diseño de Buenas Prácticas Docentes en el Contexto Actual. Alicante, España. |
| ○ | Huidobro, J. A., Méndez, A. y Serrano, M. L. (2010). Del bachillerato a la universidad: las matemáticas en las carreras de ciencia y tecnología. Aula Abierta, 38(1), 71-80. doi: http://doi.org/10.17811/rifie.38.95.2010 |
| ○ | Munns, A. (2017). A study of competence in mathematics and mechanics in an engineering curriculum. European Journal of Engineering Education, 42(6), 1062-1075. doi: 10.1080/03043797.2016.1259292 |
| ○ | Mustoe, L. y Lawson, D. (2002). A curriculum for the twenty-first century. Recuperado de http://sefi.htw-aalen.de/Curriculum/sefimarch2002.pdf |
| ○ | Nieto-Isidro, S., Martínez-Abad, F. y Rodríguez-Conde, M. J. (2017). La influencia de la elección de materias en la Prueba de Acceso a la Universidad en los conocimientos matemáticos de los estudiantes de ingeniería. Revista Complutense de Educación 28(1), 125-144. doi: http://doi.org/10.5209/rev_RCED.2017.v28.n1.48977 |
| ○ | Nortvedt, G. A. y Siqveland, A. (2019). Are beginning calculus and engineering students adequately prepared for higher education? An assessment of students’ basic mathematical knowledge. International Journal of Mathematical Education in Science and Technology, 50(3), 325-343. |
| ○ | Oliva, J. M., Franco, R. y Gil, M. L. (2018). Influencia de las pruebas de acceso a la universidad en la metodología docente del profesorado de ciencias. Ápice. Revista de Educación Científica, 2(1), 1-17. doi: http://doi.org/10.17979/arec.2018.2.1.3197 |
| ○ | Ordóñez, L. y Contreras, A. (2011). La integral definida en bachillerato: restricciones institucionales de las pruebas de acceso a la universidad. En M. Marín, G. Fernández, L. J. Blanco y M. Palarea (eds.), Investigación en Educación Matemática XV (pp. 461-470). Ciudad Real: Sociedad Española de Investigación en Educación Matemática. Recuperado de http://www.seiem.es/docs/actas/15/Actas15SEIEM.pdf |
| ○ | Riaguas, A., Arribas, M., Celorrio, R. y Lerís, D. (2006). El acceso a los estudios de ingeniería: detección de debilidades o carencias formativas en matemáticas. Actas del 4.o Congreso Internacional de Docencia Universitaria e Innovación, CIDUI. |
| ○ | Ruiz de Gauna, J. y Sarasua, J. (2011). ¿Mejoran los resultados con el nuevo sistema de selectividad? Bordón. Revista de Pedagogía, 63(4), 111-121. doi: http://doi.org/10.1016/j.aula.2015.01.002 |
| ○ | Ruiz de Gauna, J. y Sarasua, J. (2013). Estudio comparado de los resultados de las pruebas de acceso a la universidad en Cataluña, Comunidad Valenciana y País Vasco. Ikastorratza, e-Revista de Didáctica, 11, 1-24. |
| ○ | Ruiz de Gauna J., Dávila, P., Extebarría, J. y Sarasua, J. (2013). Pruebas de selectividad en matemáticas en la UPV-EHU. Resultados y opiniones de los profesores. Revista de Educación, 362, 217-246. |
| ○ | Treacy, P. y Faulkner, F. (2015). Trends in basic mathematical competencies of beginning undergraduates in Ireland, 2003-2013. International Journal of Mathematical Education in Science and Technology, 46(8), 1182-1196. doi: http://doi.org/10.1080/0020739X.2015.1050707 |
| ○ | Treacy, P., Faulkner, F. y Prendergast, M. (2016). Analysing the correlation between secondary mathematics curriculum change and trends in beginning undergraduates’ performance of basic mathematical skills in Ireland. Irish Educational Studies, 35(4), 381-401. doi: http://doi.org/10.1080/03323315.2016.1243067 |
| ○ | Zuazua E. y Rodríguez del Río, R. (2002). Enseñar y aprender matemáticas: del instituto a la universidad. Revista de Educación, 329, 239-256. |
Mathematical knowledge when accessing the university. A diachronic study (1999-2017) with Engineer students
INTRODUCTION. Although there are several studies on the mathematical knowledge of students who access university in Spain; those that cover long periods of time and that take into account the legislation about accessing university at each stage are scarce. METHOD. This study analyses the results of a basic calculus questionnaire carried out by 627 students accessing 8 undergraduate degrees of engineering for a period of 18 years —from 1999 to 2017— following two regulations for university admissions, which correspond to stages 1999-2010 and 2011-2017. The applied instrument included theoretical and practical questions, from which seven items related to logarithms, exponentials, derivation and integration have been selected. A diachronic study is carried out by grouping the data in eight biennia, five with the first regulation and three with the second, by means of proportions’ calculus and inferential analysis, including the study of effect size. RESULTS. Students have statistically different behaviour at each legislative stage, and the legislation for the stage 2011-2017 allows the generation of groups with different knowledge according to their choices and/or results in the university access examinations. The type of mathematical knowledge involved in the selected items is also relevant, showing better results in logarithms and exponentials and worse results in integration. DISCUSSION. The great variability of the mathematical level of the students who access undergraduate engineering degrees is shown, as well as the influence of the accessing legislation; those results could serve as reference for the design of future university entry examinations.
Keywords: University entry examinations, Mathematics, Educational legislation, Educational assessment.
Les connaissances mathématiques au moment de rentrer à l’Université. Une étude diachronique (1999-2017) avec des étudiants en ingénierie
INTRODUCTION. Bien qu’il y en ait de diverses études sur les connaissances mathématiques des étudiants qui accèdent à l’université en Espagne, il y en a très peu qui couvrent de longs périodes de temps et prennent en compte la législation sur l’accès à chaque période. MÉTHODE. Les réponses sont analysées dans un test objectif de calcul de base sur 626 nouveaux étudiants en huit diplômes d`ingénieur pendant 18 ans, de 1999 à 2017, suivant deux règlements d`accès à l`université en vigueur aux étapes 1999-2009 et 2010 -2017. L’ instrument appliqué comprenait des questions théoriques et pratiques, parmi lesquelles on a sélectionné sept items liés aux logarithmes, exponentielles, dérivation et intégration. On a fait une étude diachronique en regroupant les données dans huit exercices biennaux, cinq avec la première norme, et trois avec la seconde, en calculant les proportions et l`analyse différentielle, y compris la taille de l’effet. RÉSULTATS. Les étudiants présentent des comportements statistiquement différents à chaque étape législative, et la législation en vigueur en 2011-2017 permet la génération de groupes avec des connaissances différentes selon leurs choix et/ou résultats de la Preuve d’Accès à l’Université. Le type de contenu Mathématique de chaque élément sélectionné est également pertinent, montrant les meilleurs résultats en logarithmes et en exponentiels, et les plus mauvais résultats en intégration. DISCUSSION. On a montré la grande variabilité du niveau de connaissance mathématique des étudiants qui accèdent à des études en ingénierie et l’influence de la législation sur l`accès à ces connaissances ; ces résultats peuvent être une référence pour la conception de futures preuves d’accès à l’université.
Mots-clés: Accès aux études université, Mathématiques, Législation éducative, Evaluation éducative.
Susana Nieto-Isidro (autora de contacto)
Profesora titular, miembro del Departamento de Matemática Aplicada del Instituto Universitario de Ciencias de la Educación de la Universidad de Salamanca y doctora en Ciencias Matemáticas por la Universidad de Salamanca. Sus intereses investigadores se centran en la docencia de las matemáticas en diferentes niveles educativos, en el diseño y evaluación de programas formativos y en la innovación docente para la enseñanza-aprendizaje de las matemáticas. Forma parte de la unidad consolidada de investigación GRIAL.
Correo electrónico de contacto: sni@usal.es
Dirección para la correspondencia: calle Parque, 2, 37008 Salamanca.
Fernando Martínez-Abad
Profesor contratado doctor, miembro del Departamento de Didáctica, Organización y Métodos de Investigación del Instituto Universitario de Ciencias de la Educación de la Universidad de Salamanca y doctor sobresaliente cum laude en Ciencias de la Educación (Premio Extraordinario). Sus líneas de investigación se centran en la evaluación de competencias, los métodos de investigación en tecnología educativa y el análisis de datos en educación. Como parte de la unidad consolidada de investigación GRIAL, ha participado en numerosos proyectos de investigación nacionales e internacionales, siendo beneficiario de una de las prestigiosas becas Leonardo (Fundación BBVA).
Correo electrónico de contacto: fma@usal.es
María José Rodríguez-Conde
Catedrática de universidad, miembro del Departamento de Didáctica, Organización y Métodos de Investigación del Instituto Universitario de Ciencias de la Educación de la Universidad de Salamanca, directora del Instituto Universitario de Ciencias de la Educación de la Universidad de Salamanca e investigadora principal del grupo de investigación reconocido Grupo de Evaluación Educativa y Orientación (GE2O). Investigadora principal en numerosos proyectos de investigación nacionales y participante en diversos proyectos europeos y contratos de investigación. Miembro de la unidad consolidada de investigación GRIAL.
Correo electrónico de contacto: mjrconde@usal.es