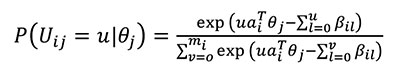 (1)
(1)XAVIER G. ORDÓÑEZ CAMACHO(1), DELIA ARROYO RESINO(2) Y COVADONGA RUIZ DE MIGUEL(1)
(1) Universidad Complutense de Madrid
(2) Universidad Internacional de La Rioja
DOI: 10.13042/Bordon.2019.66880
Fecha de recepción: 26/07/2018 • Fecha de aceptación: 16/04/2019
Autora de contacto / Corresponding author: Covadonga Ruiz de Miguel. E-mail: covaruiz@ucm.es.
INTRODUCCIÓN. Recientemente Ordóñez, Romero y Ruiz de Miguel (2016) han propuesto el Cuestionario de Actitudes Hacia la Estadística (CAHE) el cual tiene evidencia de validez y de fiabilidad. Sin embargo, requiere de un análisis más exhaustivo de los ítems para ampliar la evidencia de validez de los mismos en las distintas dimensiones. MÉTODO. Por ello, en el presente estudio el objetivo es ampliar la evidencia de la calidad psicométrica del CAHE, a través de la aplicación del Modelo Multidimensional de Crédito Parcial Generalizado (MMCPG). Se aplicó el CAHE a una muestra incidental compuesta por 836 estudiantes de la Facultad de Educación, de la Universidad Complutense de Madrid. El CAHE está compuesto por tres dimensiones: la escala de emociones negativas, la escala de emociones positivas y la escala de utilidad, con un total de 16 ítems en escala tipo Likert con 5 opciones de respuesta que van desde “completamente en desacuerdo” a “completamente de acuerdo”. Para el análisis de los ítems se ha utilizado el programa R versión 3.4.3. RESULTADOS. Los resultados muestran que el cuestionario se comporta siguiendo una estructura de 3 dimensiones donde cada uno de los ítems en cada una de las dimensiones, presenta adecuados valores en los parámetros de discriminación y dificultad. DISCUSIÓN. Por lo tanto, los resultados permiten ampliar la validez reportada anteriormente, siendo, hasta la fecha, una de las pocas pruebas con evidencia de validez a nivel de constructo y de ítems.
Palabras clave: Modelo Multidimensional de Crédito Parcial Generalizado (MMCPG), actitudes, estadística, Teoría de Respuesta al Ítem (TRI), Estudiantes universitarios, escala Likert.
Actualmente, la estadística es una materia incorporada a la mayoría de los planes de estudio de las carreras universitarias y, tradicionalmente, las actitudes de los estudiantes hacia esta asignatura son negativas o neutras (Estrada, Batanero y Fortuny, 2006Estrada, A., Batanero, C. y Fortuny, J. (2006). Análisis de las actitudes y conocimientos estadísticos elementales en la formación del profesorado. Tarbiya, 38, 79-90. ), especialmente en las titulaciones del área de las ciencias sociales, como los profesores en formación, los estudiantes de Pedagogía o Educación Social.
Las actitudes son un fenómeno de difícil definición al ser construcciones teóricas que se infieren de ciertos comportamientos externos, frecuentemente verbales (Mc Leod, 1994Mc Leod, D. B. (1994). Research on affect and mathematics learning in the JRME: 1970 to the present. Journal for Research in Mathematics Education, 25(6), 637-647. doi: 10.2307/749576). Su conceptualización ha ido variando a lo largo del tiempo; así para Auzmendi son “aspectos no directamente observables sino inferidos, compuestos por creencias, sentimientos y predisposiciones comportamentales hacia el objeto al que se dirigen” (1992Auzmendi, E. (1992). Las actitudes hacia la matemática estadística en las enseñanzas medias y universitarias. Bilbao: Mensajero.: 17); Gómez Chacón las entiende como uno de los componentes básicos del dominio afectivo y las define como: “una predisposición evaluativa (positiva o negativa) que determina las intenciones personales e influye en el comportamiento” (2000Gómez Chacón, I. (2000). Matemática emocional. Los afectos en el aprendizaje matemático. Madrid: Narcea.: 23). Phillips (2007Phillips, R. (2007). Mathematics teachers’ beliefs and affects. En F. Lester, Second Handbook of Research on Mathematics Teaching and Learning (pp. 257-315). Charlotte: Information Age Publishing and National Council of Teachers of Mathematics.) las describe como “formas de actuar, sentir o pensar que muestran la disposición u opinión de una persona”. Más recientemente, Syyeda (2016Syyeda, F. (2016). Understanding Attitudes Towards Mathematics (ATM) using a Multi-modal Model: An Exploratory Case Study with Secondary School Children in England. Cambridge Open-Review Educational Research e-Journal, 3, 32-62. Recuperado de http://corerj.soc.srcf.net/?page_id=224) considera que la actitud se refiere a la “tendencia aprendida de una persona a responder positiva o negativamente hacia un objeto, situación, concepto u otra persona pudiendo cambiar y desarrollarse con el tiempo”. A la vista de estas definiciones parece no existir una única conceptualización de este fenómeno. Para la presente investigación, siguiendo a Ordóñez et al. (2016Ordóñez, X., Romero, R. y Ruiz, C. (2016). Cuestionario de Actitudes Hacia la Estadística (CAHE): evidencias de validez y fiabilidad de las puntuaciones en una muestra de alumnos de Educación. Bordón, 68(4), 121-136. doi: 10.13042), se considera que las actitudes son un “conjunto de predisposiciones inferidas que orientan las acciones personales”.
Una actitud negativa dificulta el aprendizaje efectivo y, por lo tanto, podría incidir en el logro de superar la materia, e incluso de incorporarla a nivel profesional (García-Martínez, Fallas-Vargas y Romero-Hernández, 2015García-Martínez, J., Fallas-Vargas, M. y Romero-Hernández, A. (2015). Las actitudes hacia la estadística del estudiantado de orientación. Revista Electrónica Educare, 19(1), 25-41. doi: 10.15359/ree.19-1.2). Así, la actitud es un factor fundamental que no puede ser ignorado. En el caso de la estadística, en ocasiones, expresan sentimientos vinculados a elementos que no son parte de la materia, como el profesor o el tipo de actividad que se realiza (Comas, Martins, Nascimento y Estrada, 2017Comas, C., Martins, J., Nascimento, M. y Estrada, A. (2017). Estudio de las Actitudes hacia la Estadística en Estudiantes de Psicología. Boletim de Educação Matemática, 31(57). doi: 10.1590/1980-4415v31n57a23). Parece que el origen de las actitudes hacia la estadística (hacia las matemáticas en general) podría estar en una serie de factores cruzados relacionados con los estudiantes (Tshabalala y Ncube, 2016Tshabalala, T. y Ncube, A. C. (2016). Causes of poor performance of ordinary level pupils in mathematics in rural secondary schools in Nkayi district: Learner’s attributions. Nova Journal of Medical and Biological Sciences, 15(1), 122-136.), como son las experiencias previas de los mismos (Ngussa y Mbuti, 2017Ngussa, B. M. y Mbuti, E. E. (2017). The Influence of Humour on Learners’ Attitude and Mathematics Achievement: A Case of Secondary Schools in Arusha City, Tanzania. Journal of Educational Research, 2(3), 170-181. ), con factores ambientales o escolares, como el clima del aula, el entorno familiar o las expectativas de los padres sobre el rendimiento de sus hijos (Chang y Beilock, 2016Chang, H. y Beilock, S. L. (2016). The math anxiety-math performance link and its relation to individual and environmental factors: a review of current behavioral and psychophysiological research. Current Opinion in Behavioral Sciences, 10, 33-38. doi: 10.1016/j.cobeha.2016.04.011), y con los métodos de enseñanza de los docentes (Ngussa y Mbuti, 2017Ngussa, B. M. y Mbuti, E. E. (2017). The Influence of Humour on Learners’ Attitude and Mathematics Achievement: A Case of Secondary Schools in Arusha City, Tanzania. Journal of Educational Research, 2(3), 170-181. ), entre otros posibles.
Existen numerosos instrumentos para medir las actitudes hacia la estadística, puede verse una recopilación en Blanco (2008Blanco, A. (2008). Una revisión crítica sobre la investigación sobre las actitudes de los estudiantes universitarios hacia la estadística. Revista Complutense de Educación, 19(2), 311-330.). Los más utilizados son: la escala SAS (Roberts y Bilderback, 1980Roberts, D. M. y Bilderback, E. W. (1980). Reliability and validity of a statistics attitude survey. Educational and Psychological Measurement, 40, 235-238. doi: 10.1177/001316448004000138), la ATS (Wise, 1985Wise, S. (1985). The development and validation of a scale measuring attitudes toward statistics. Educational and Psychological Measurement 2(45), 401-405. doi: 10.1177/001316448504500226) y la SATS (Schau, Stevens, Dauphine y Del Vecchio, 1995Schau, C., Stevens, J., Dauphine, T. y Del Vecchio, A. (1995). The development and validation of the survey of attitudes towards statistics. Educational and Psychological Measurement, 55(5), 868-875. doi: 10.1177/0013164495055005022). Uno de los últimos instrumentos propuestos para la medición de las actitudes hacia la estadística es el Cuestionario de Actitudes Hacia la Estadística (CAHE), propuesto por . Este instrumento tiene tres escalas: emociones negativas, que se puede entender como seguridad ante la estadística; emociones positivas, sentimientos o emociones que se presentan a la hora de trabajar con la estadística; y utilidad, referida al posible uso que los estudiantes consideran que tendrá la estadística en su vida profesional. Ordóñez et al. (2016Ordóñez, X., Romero, R. y Ruiz, C. (2016). Cuestionario de Actitudes Hacia la Estadística (CAHE): evidencias de validez y fiabilidad de las puntuaciones en una muestra de alumnos de Educación. Bordón, 68(4), 121-136. doi: 10.13042) reportan evidencia de validez de constructo y de fiabilidad del CAHE a través del Análisis Factorial Exploratorio (AFE) y Confirmatorio (AFC) —de primer y segundo orden—, afirmando que es un instrumento adecuado para la medición de las actitudes hacia la estadística.
El objetivo de la presente investigación es ampliar la evidencia de la calidad psicométrica del CAHE, y para ello se realizará un análisis detallado de los ítems, a través de la aplicación del Modelo Multidimensional de Crédito Parcial Generalizado (MMCPG) de la Teoría de Respuesta a los Ítems (TRI), ya que la estructura del CAHE es multidimensional.
El análisis de los ítems de las pruebas de actitudes hacia la estadística a través de modelos de TRI no ha sido muy frecuente. Tarazona, Bazán y Aparicio (2013Tarazona, E., Bazán, J. y Aparico, A. (2013). Actitudes hacia la estadística en universitarios peruanos de mediana edad. Revista Digital de Investigación en Docencia Universitaria, 1, 58-76.) analizan las propiedades psicométricas de los ítems en una muestra de estudiantes universitarios peruanos en dos instrumentos: Actitudes hacia la Estadística (AEE), de Estrada (2002Estrada, A. (2002). Análisis de las actitudes y conocimientos estadísticos elementales en la formación del profesorado (tesis doctoral). Universitat Autònoma de Barcelona, Barcelona.), y Actitudes hacia la Estadística (AEC), de Cazorla, Silva, Vendramini y Brito (1999Cazorla, I., Silva da, C., Vendramini, C. y Brito, M. (1999). Adaptación y validación de una escala de actitudes hacia la estadística. En Conferência Internacional: Experiências e expectativas do Ensino da Estatística (pp. 45-58). Florianópolis, Brasil.), a través del Modelo de Respuesta Graduada (MRG) (Samejima, 1969Samejima, F. (1969). Estimation of latent ability using a response pattern of graded scores. Psychometrika Monograph, 17, 3-21.), de la TRI. Vendramini, Silva y Dias (2009Vendramini, C. M. M., Silva, M. C. R. D. y Dias, A. S. (2009). Assessment of psychology students' attitudes through credit partial model of IRT. Psico-USF, 14(3), 287-298. doi: 10.1590/S1413-82712009000300005) verificaron las propiedades psicométricas de una escala de actitudes hacia la estadística, adaptación de la escala de Aiken y Dreger (1961Aiken, L. R. y Dreger, R. M. (1961). El efecto de las actitudes en el desempeño en Mathematics. Diario de Psicología de la Educación, 52(1), 19-24.), en estudiantes de Psicología, pero en este caso mediante un Modelo de Crédito Parcial (MCP) de la TRI.
Por el contrario, son más comunes los estudios que han realizado aplicaciones de modelos de TRI en escalas de actitudes hacia las matemáticas y sus subdimensiones, muestra de ello es, por ejemplo, la investigación de Abal, Auné, Lozzia y Attorresi (2015Abal, F. J. P., Auné, S. E., Lozzia, G. S. y Attorresi, H. F. (2015). Modelización de una prueba de afecto hacia la matemática con la teoría de respuesta al ítem. Revista de Psicología, 11(21), 23-34. Recuperado de http://bibliotecadigital.uca.edu.ar/repositorio/revistas/modelizacion-prueba-afecto-matematica.pdf), quienes aplicaron un MCP al análisis de ítems de la escala Afectos hacia las Matemáticas. Más recientemente Rodríguez y Mora (2016Rodríguez, O. y Mora, S. (2016). Análisis psicométrico del instrumento Actitudes hacia las Matemáticas mediante el modelo de Respuesta Graduada de Samejima. Actualidades en Psicología, 30(120), 7-30. doi: 10.15517/ap.v30i120.18722) realizaron un análisis psicométrico del instrumento llamado Actitudes hacia las Matemáticas (instrumento original de Bazán y Sotero, 1998Bazán, J. L. y Sotero, H. (1998). Una aplicación al estudio de actitudes hacia la matemática en la UNALM. Revista Anales Científicos. UNALM, 36(1), 60-72.) en estudiantes universitarios, ajustando un MRG a partir de la Teoría Clásica de los Test (TCT). También Palacios, Arias y Arias (2014Palacios, A., Arias, V. y Arias, B. (2014). Actitudes hacia las matemáticas: construcción y validación de un instrumento de medición. Revista de Psicodidáctica, 19(1), 67-91. doi: 10.1387 / RevPsicodidact.8961) aplicaron un MRG a la Escala de Actitudes hacia las Matemáticas (EAM) en estudiantes no universitarios.
Sin embargo, no es tan común el uso de modelos multidimensionales de la TRI ni, más concretamente, la aplicación del Modelo Multidimensional de Crédito Parcial Generalizado (MMCPG) a ítems que midan las actitudes hacia la estadística.
El MMCPG de la TRI, propuesto por Yao y Schwarz (2006Yao, L. y Schwarz, R. D. (2006). A multidimensional partial credit model with associated item and test statistics: An application to mixed-format tests. Applied Psychological Measurement, 30(6), 469-492. ), se aplica en test formados por ítems politómicos con categorías ordenadas. Es especialmente adecuado en ítems pertenecientes a escalas de actitudes donde las categorías se puntúan con un valor discreto entre 1 y el número de categorías del ítem, lo que supone que la elección de las categorías más altas implica una actitud más favorable. También es correcta su aplicación cuando existe más de un rasgo latente, correlacionados, que puede explicar la probabilidad de elegir una categoría en particular.
La probabilidad de seleccionar la categoría ordenada u con un vector de rasgo latente θ de la persona j viene dada por:
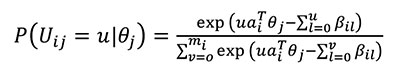 (1)
(1)
Donde u = 0, 1,…mi es la categoría seleccionada por el sujeto j en el ítem i y mi es la categoría más alta para el ítem i. βil es el parámetro de umbral para la categoría u, βi0 =0, θ y a son los vectores del rasgo latente y discriminación, respectivamente. Por lo tanto, se deben estimar para el modelo mi, parámetros βil y un vector de parámetros a que depende del número de dimensiones, correlacionadas, que se requieran para dar respuesta al ítem.
El MMCPG es una generalización del Modelo de Crédito Parcial Generalizado (MCPG) (Muraki, 1992Muraki, E. (1992). A generalized partial credit model: Application of an EM algorithm. Applied Psychological Measurement, 16, 159-176.) de la TRI. Difiere del mismo en dos aspectos importantes: el primero de ellos es que a diferencia del MCPG, el MMCPG no incluye los parámetros de dificultad y de umbral separadamente. Y el segundo es que como θ es un vector, mientras que las β son escalares, no es posible substraer el parámetro de umbral del vector de thetas del MMCPG (Reckase, 2009Reckase, M. D. (2009). Multidimensional item response theory. New York: Springer.).
Dentro del MMCPG son dos los parámetros fundamentales, los de umbral y la discriminación. Los parámetros de umbral (βil) están asociados a la dificultad de las categorías del ítem y son valores que están expresados en la misma métrica que θ. El vector a, referido a la discriminación, indica la asociación del ítem con el rasgo. Valores positivos de a permiten afirmar que las categorías más altas del ítem serán elegidas por aquellas personas que tengan altos niveles en theta. Además, este parámetro de discriminación se relaciona con el apuntamiento y el estrechamiento de las Funciones de Respuesta al Ítem, ya que, a mayor parámetro de discriminación, mejor se diferencian las categorías de respuesta entre los diferentes niveles del rasgo (Abad, Ponsoda y Revuelta, 2006Abad, F., Ponsoda, V. y Revuelta, J. (2006). Modelos politómicos de respuesta al ítem. Madrid: La Muralla.).
Por otro lado, dentro del MMCPG es posible conocer la Función de Información del Ítem (FII) y la Función de Información del Test (FIT). La FII indica la precisión con la que el ítem estima los diferentes niveles de rasgo y el FIT es la suma de las funciones de información de los ítems.
El MMCPG es adecuado para el presente estudio debido a que se tienen ítems politómicos con diferentes parámetros a (Post, Van Duijn y Van Baarsen, 2001Post, W. J, Van Duijn, M. A. J. y Van Baarsen, B. (2001). Tracelines de un solo pico o monótono? En la elección de un modelo IRT para escalar datos. En A. Boomsma, MAJ van Duijn y TAB Snijders (eds.), Ensayos sobre la teoría de la respuesta al ítem (pp. 391-414). Nueva York: Springer.), y se tienen ítems que están en una escala Likert (Ostini y Nering, 2006Ostini, R. y Nering, M. L. (2006). Polytomous item response theory models. London: Sage pub., 2010Ostini, R. y Nering, M. L. (2010). Handbook of Polytomous item response theory models. London: Taylor & Francis Group.).
Objetivo
El objetivo del presente trabajo es analizar las propiedades psicométricas de los ítems que conforman las tres escalas (emociones negativas, emociones positivas y utilidad) del CAHE a través del MMCPG (Yao y Schwarz, 2006Yao, L. y Schwarz, R. D. (2006). A multidimensional partial credit model with associated item and test statistics: An application to mixed-format tests. Applied Psychological Measurement, 30(6), 469-492. ) de la TRI.
Participantes
Este trabajo se ha realizado con una muestra incidental compuesta por 836 estudiantes del primer curso de grado de la Universidad Complutense de Madrid, que cursan las asignaturas de Estadística Aplicada a las Ciencias Sociales y Métodos de Investigación Educativa. Un 15,1% pertenecían al grado de Pedagogía, un 12,9% al de Educación Social, un 37,1% a Educación Primaria y el 35% restante a Educación Infantil. Los estudiantes matriculados por primera vez son el 82,5%, y el 16,8% restante se ha matriculado dos o más veces. De la muestra total un 15% eran hombres y un 80% mujeres, el resto no se identificaron (5%). Los estudiantes han participado en el estudio de forma voluntaria, y mediante el consentimiento informado se ha garantizado que los resultados fueran tratados de forma ética y anónima. Los datos se recogieron a través de un cuestionario en formato papel aplicado en el aula durante la hora de clase, previo acuerdo con los profesores. En este trabajo se hace una segunda explotación de los datos utilizados en Ordóñez et al. (2016Ordóñez, X., Romero, R. y Ruiz, C. (2016). Cuestionario de Actitudes Hacia la Estadística (CAHE): evidencias de validez y fiabilidad de las puntuaciones en una muestra de alumnos de Educación. Bordón, 68(4), 121-136. doi: 10.13042).
Instrumento
La prueba utilizada ha sido el CAHE, que tiene evidencia de validez y de fiabilidad. Según un AFC realizado por Ordóñez et al. (2016Ordóñez, X., Romero, R. y Ruiz, C. (2016). Cuestionario de Actitudes Hacia la Estadística (CAHE): evidencias de validez y fiabilidad de las puntuaciones en una muestra de alumnos de Educación. Bordón, 68(4), 121-136. doi: 10.13042), el cuestionario está compuesto por una estructura tridimensional correlacionada; la escala de emociones negativas (EN) consta de 8 ítems (α = 0.921), la escala de emociones positivas (EP) está formada por 4 ítems (α = 0.774) y la escala de utilidad (U) está compuesta por 4 ítems (α = 0.745). El instrumento utilizado muestra un ajuste al modelo de segundo orden (actitud) (χ²=123.20, gl=101, p=.066; RMSEA=.024; CFI=NNFI=1; SRMR=.045). Ordóñez et al. (2016Ordóñez, X., Romero, R. y Ruiz, C. (2016). Cuestionario de Actitudes Hacia la Estadística (CAHE): evidencias de validez y fiabilidad de las puntuaciones en una muestra de alumnos de Educación. Bordón, 68(4), 121-136. doi: 10.13042) reportan también una escala con todos los ítems llamada actitud hacia la estadística (α = 0.902). El instrumento está formado por un total de 16 ítems, que se responden en una escala tipo Likert con 5 opciones de respuesta, que varían desde “completamente en desacuerdo” hasta “completamente de acuerdo”.
Procedimiento y análisis de datos
Las propiedades psicométricas de los ítems del CAHE se estimaron a través del MMCPG. Se realiza el análisis empleando todos los ítems de la prueba, teniendo en cuenta que la validez de constructo sustenta que existen tres dimensiones que explican las actitudes hacia la estadística. Los parámetros de los ítems fueron estimados a través del método EM (esperanza-maximización), y el ajuste del MMCPG a los datos se realizó a través del estadístico M2 (Maydeu-Olivares y Joe, 2006Maydeu-Olivares, A. y Joe, H. (2006). Limited information goodness-of-fit testing in multidimensional contingency tables. Psychometrika, 71, 713-732.), ya que siguiendo a Montaño (2009Montaño, R. (2009). Una comparación de las estadísticas de bondad de ajuste R1 y M2 para modelos de la Teoría de Respuesta al Ítem (tesis doctoral no publicada). Universidad de Barcelona, Barcelona.) se considera que el estadístico M2 es adecuado para analizar el ajuste de los modelos de la TRI a los datos, puesto que este presenta un mejor manejo de las tasas nominales del error de tipo I. Además, los estadísticos: Root Mean Square Error of Approximation (RMSEA), Standardized Root Mean Square Residual (SRMSR), Comparative Fit Index (CFI), Tucker-Lewis Index (TLI), Akaike Information Criterion (AIC) y Bayesian Information Criterion (BIC) fueron empleados para analizar dicho ajuste. También se utilizaron los estadísticos Zh (Drasgow, Levine y Williams, 1985Drasgow, F., Levine, M. V. y Williams, E. A. (1985). Appropriateness measurement with polychotomous item response models and standardized indices. British Journal of Mathematical and Statistical Psychology, 38, 67-86.) y S-X2 (Orlando y Thissen, 2000Orlando, M. y Thissen, D. (2000). Likelihood-based item fit indices for dichotomous item response theory models. Applied Psychological Measurement, 24, 50-64.; Kang y Chen, 2007Kang, T. y Chen, T. T. (2007). An investigation of the performance of the generalized S-X2 item-fit index for polytomous IRT models. ACT Research Report Series.) para valorar el ajuste en cada uno de los ítems.
Software
En el análisis de los ítems se ha utilizado el programa R versión 3.4.3 (R Core Team, 2017R Core Team (2017). R: A language and environment for statistical computing. Foundation for statistical Computing. Vienna, Austria. Recuperado de http://www.r-project.org/) a través de RStudio versión 1.1.453 (RStudio Team, 2018RStudio Team (2018). RStudio: Integrated Development for R. RStudio, Inc. Boston, Massachusetts. Recuperado de http://www.rstudio.com/), usando el paquete Mirt (Chalmers, 2012Chalmers, R. P. (2012). Mirt: A Multidimensional Item Response Theory Package for the R Environment. Journal of Statistical Software, 48(6), 1-29. doi: 10.18637/jss.v048.i06) versión 1.28.
A continuación, se presentan los resultados del estudio. En primer lugar, se analiza si el MMCPG se ajusta al conjunto de datos. En segundo lugar, se estudia el ajuste del modelo a cada uno de los ítems acompañados de los parámetros estimados y, por último, los resultados de la Función de Información del Test (FIT) para identificar en qué valores del vector θ el test es más informativo.
Ajuste del MMCPG a los datos
El ajuste del modelo a los datos se estudia a través de una prueba de hipótesis de razón de verosimilitud (Likelihood Ratio Test) entre un MMCPG con una única dimensión y un MMCPG con las tres dimensiones del CAHE.
El MMCPG con una única dimensión presenta un M2 = 125.73 (gl= 56 y p<0.001), RMSEA = 0.038 (IC=0.95 entre 0.029 y 0.047), SRMSR = 0.101, TLI = 0.970 y CFI = 0.976, AIC = 34009.40, BIC = 34389.49 y Log Likelihood = -16924.70. Según el M2 este modelo no presenta un ajuste a los datos.
El MMCPG con las tres dimensiones del CAHE un M2 = 69.384 (gl= 53 y p>0.05), RMSEA = 0.019 (IC=0.95 entre 0 y 0.030), SRMSR = 0.043, TLI = 0.992 y CFI = 0.994, AIC = 32919.09, BIC = 33313.43 y Log Likelihood = -16376.54. Según el M2 en este modelo de tres dimensiones se observa un ajuste del MMCPG a los datos.
La prueba de hipótesis de razón de verosimilitud arroja un χ2 = 1096.314 (gl= 3 y p <0.001), lo cual demuestra que el modelo de tres dimensiones es estadísticamente diferente al modelo unidimensional, por lo tanto, los datos se comportan siguiendo una estructura de tres dimensiones.
Ajuste del MMCPG a los ítems y parámetros
En la tabla 1 se presentan los resultados de los estadísticos de ajuste de cada uno de los ítems de la prueba CAHE y sus parámetros, tanto para el vector a como los de umbral (β). En primer lugar, según el estadístico Zh hay 3 ítems en los que el MMCPG no se ajusta a los datos (6, 10 y 12), y según el estadístico S-X2 hay 6 que no se ajustan (5, 7, 8, 10, 12 y 14) a una p<0.05, sin embargo, no se puede afirmar que sea un desajuste considerable que amerite que los ítems sean eliminados de la prueba.
Con respecto a los parámetros del vector a, se puede afirmar que: primero, que los parámetros más altos se observan en la dimensión EP y los más bajos en la dimensión U. Segundo, que la media de los errores estándar de los parámetros es más alta en la dimensión EP (x̅es = 0.16) que con respecto a EN y U (x̅es = 0.11, en cada una), es decir, los parámetros a en EP son más imprecisos. Y tercero, en la dimensión EN se observa que el ítem que más discrimina es el ítem 3 (“Trabajar con la estadística hace que me sienta muy nervioso/a”) y el que menos es el ítem 1 (“La asignatura de Estadística se me da bastante mal”), para la dimensión EP el ítem que más discrimina es el ítem 11 (“La estadística es agradable y estimulante para mí”) y el que menos el ítem 12 (“Me gustaría tener una ocupación en la cual tuviera que utilizar la estadística”) y para la dimensión U el ítem que más discrimina es el ítem 16 (“En mi profesión no usaré estadística”) y el que menos el ítem 14 (“La estadística es un requisito en mi formación como profesional”), que a su vez es el que tiene menos poder de discriminación de todos los ítems.
Con respecto a los parámetros de umbral (β), se puede afirmar que: primero, en los ítems de la dimensión EP se observa que en la mayoría de los mismos el comportamiento de los parámetros β sigue un ordenamiento creciente (a excepción del ítem 11), que es lo esperado para estos parámetros; mientras que los parámetros β de los ítems de las otras dimensiones registran inversiones, por ejemplo, los β del ítem 2 de EN. Segundo, en general, los errores estándar de los parámetros β son más altos a medida que aumenta el número de la categoría, por ejemplo, el ítem 14 de la dimensión U. Tercero, los parámetros β4 más altos se observan en los ítems de la dimensión EP, lo cual puede estar diciendo que existen serias dificultades de su estimación debido a que no hay suficientes datos en las categorías más altas que permitan una buena estimación de dicho parámetro. Y cuarto, se observa que el nivel de theta mínimo requerido para elegir entre categorías es 0.013 y el máximo 8.827, es decir, nivel que va desde la media a lo más alto, en otras palabras, las dificultades de los ítems tienden a ser altas.
Los resultados de los parámetros de los ítems permiten afirmar que tenemos ítems que discriminan muy bien a las personas con bajas y altas actitudes hacia la estadística y, a su vez, que se requiere un nivel medio-alto de habilidad para elegir las categorías de los ítems más altas, es decir, las personas deben tender a poseer una actitud alta.
| Tabla 1. Estadísticos de ajuste y parámetros de los ítems en el MMCPG | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Función de Información del Test
Con respecto a la FIT, en la figura 1 se observa su contorno y, concretamente, en la figura con la etiqueta A se aprecia en qué niveles del vector θ se obtiene una mayor precisión en el test. Dichos valores corresponden a θEN = 0.00, θEP = 1.90 y θU = -1.20 con un valor máximo en FIT de 13.989. Por lo tanto, el test es más informativo para niveles medios de emociones negativas, niveles altos de emociones positivas y niveles bajos en utilidad.
|
Figura 1. Contorno de la FIT 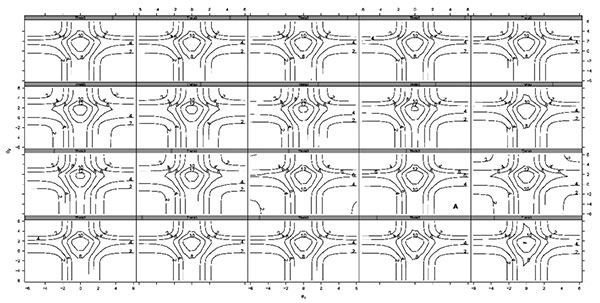
|
A la vista de los resultados se puede afirmar que los ítems que conforman el CAHE presentan evidencia de validez según el MMCPG, donde cada uno de los ítems, para cada una de las tres dimensiones, presenta adecuados valores en los parámetros de discriminación y dificultad. Por lo tanto, los resultados permiten ampliar la evidencia de validez reportada anteriormente por Ordóñez et al. (2016Ordóñez, X., Romero, R. y Ruiz, C. (2016). Cuestionario de Actitudes Hacia la Estadística (CAHE): evidencias de validez y fiabilidad de las puntuaciones en una muestra de alumnos de Educación. Bordón, 68(4), 121-136. doi: 10.13042) para la prueba CAHE. Siendo, hasta la fecha, una de las pocas pruebas que presentan evidencia de validez a nivel de constructo y de ítems con respecto a las otras pruebas para la medición de las actitudes hacia la estadística.
Sin embargo, la limitación más importante que tiene el presente estudio tiene que ver con el hecho de haberse usado los mismos datos de Ordóñez et al. (2016Ordóñez, X., Romero, R. y Ruiz, C. (2016). Cuestionario de Actitudes Hacia la Estadística (CAHE): evidencias de validez y fiabilidad de las puntuaciones en una muestra de alumnos de Educación. Bordón, 68(4), 121-136. doi: 10.13042), no por ser los mismos datos en sí, sino por la falta de representatividad de la muestra; es decir, los datos provienen, en su totalidad, de una muestra incidental de estudiantes de la Facultad de Educación de la UCM. El hecho de haber usados datos que vienen de una muestra no representativa tiene como consecuencia que los resultados obtenidos no puedan ser generalizados a la población objetivo; en otras palabras, la validez de los mismos tienen las mismas limitaciones de todos los estudios que trabajan con muestras no representativas. Por lo tanto, se sugiere replicar el estudio en una muestra representativa de estudiantes universitarios para corroborar si la calidad de los ítems de la prueba CAHE es la misma que la expuesta en el presente estudio.
Se recomienda ampliar aún más la validez de la prueba CAHE, pues, aunque hasta la fecha se tiene evidencia de validez de constructo y del análisis de los ítems, se hace necesario analizar si la estructura factorial es invariante entre distintos tipos de estudiantes universitarios y entre estudiantes universitarios de distintos países. A su vez, si los parámetros de los ítems según el MMCPG se mantienen invariantes o no entre estas poblaciones. También, si existe funcionamiento diferencial del ítem (DIF) entre, por ejemplo, hombres y mujeres, o entre estudiantes de distintas facultades (Educación y Ciencias). En conclusión, seguir obteniendo evidencia de la calidad psicométrica de la prueba CAHE, con el fin de crear un instrumento lo suficientemente válido y fiable que contribuya a diseñar programas de diagnóstico e intervención que reduzcan los posibles efectos negativos que tienen las actitudes hacia el estudio de todo contenido relacionado con la estadística sobre el rendimiento de los estudiantes.
En conclusión, seguir obteniendo evidencia de la calidad psicométrica de la prueba CAHE, con el fin de crear un instrumento lo suficientemente válido y fiable que contribuya a diseñar programas de diagnóstico e intervención que reduzcan los posibles efectos negativos que sobre el rendimiento tienen las actitudes hacia el estudio de todo contenido relacionado con la estadística.
| ○ | Abad, F., Ponsoda, V. y Revuelta, J. (2006). Modelos politómicos de respuesta al ítem. Madrid: La Muralla. |
| ○ | Abal, F. J. P., Auné, S. E., Lozzia, G. S. y Attorresi, H. F. (2015). Modelización de una prueba de afecto hacia la matemática con la teoría de respuesta al ítem. Revista de Psicología, 11(21), 23-34. Recuperado de http://bibliotecadigital.uca.edu.ar/repositorio/revistas/modelizacion-prueba-afecto-matematica.pdf |
| ○ | Aiken, L. R. y Dreger, R. M. (1961). El efecto de las actitudes en el desempeño en Mathematics. Diario de Psicología de la Educación, 52(1), 19-24. |
| ○ | Auzmendi, E. (1992). Las actitudes hacia la matemática estadística en las enseñanzas medias y universitarias. Bilbao: Mensajero. |
| ○ | Bazán, J. L. y Sotero, H. (1998). Una aplicación al estudio de actitudes hacia la matemática en la UNALM. Revista Anales Científicos. UNALM, 36(1), 60-72. |
| ○ | Blanco, A. (2008). Una revisión crítica sobre la investigación sobre las actitudes de los estudiantes universitarios hacia la estadística. Revista Complutense de Educación, 19(2), 311-330. |
| ○ | Cazorla, I., Silva da, C., Vendramini, C. y Brito, M. (1999). Adaptación y validación de una escala de actitudes hacia la estadística. En Conferência Internacional: Experiências e expectativas do Ensino da Estatística (pp. 45-58). Florianópolis, Brasil. |
| ○ | Chalmers, R. P. (2012). Mirt: A Multidimensional Item Response Theory Package for the R Environment. Journal of Statistical Software, 48(6), 1-29. doi: 10.18637/jss.v048.i06 |
| ○ | Chang, H. y Beilock, S. L. (2016). The math anxiety-math performance link and its relation to individual and environmental factors: a review of current behavioral and psychophysiological research. Current Opinion in Behavioral Sciences, 10, 33-38. doi: 10.1016/j.cobeha.2016.04.011 |
| ○ | Comas, C., Martins, J., Nascimento, M. y Estrada, A. (2017). Estudio de las Actitudes hacia la Estadística en Estudiantes de Psicología. Boletim de Educação Matemática, 31(57). doi: 10.1590/1980-4415v31n57a23 |
| ○ | Drasgow, F., Levine, M. V. y Williams, E. A. (1985). Appropriateness measurement with polychotomous item response models and standardized indices. British Journal of Mathematical and Statistical Psychology, 38, 67-86. |
| ○ | Estrada, A. (2002). Análisis de las actitudes y conocimientos estadísticos elementales en la formación del profesorado (tesis doctoral). Universitat Autònoma de Barcelona, Barcelona. |
| ○ | Estrada, A., Batanero, C. y Fortuny, J. (2006). Análisis de las actitudes y conocimientos estadísticos elementales en la formación del profesorado. Tarbiya, 38, 79-90. |
| ○ | García-Martínez, J., Fallas-Vargas, M. y Romero-Hernández, A. (2015). Las actitudes hacia la estadística del estudiantado de orientación. Revista Electrónica Educare, 19(1), 25-41. doi: 10.15359/ree.19-1.2 |
| ○ | Gómez Chacón, I. (2000). Matemática emocional. Los afectos en el aprendizaje matemático. Madrid: Narcea. |
| ○ | Kang, T. y Chen, T. T. (2007). An investigation of the performance of the generalized S-X2 item-fit index for polytomous IRT models. ACT Research Report Series. |
| ○ | Maydeu-Olivares, A. y Joe, H. (2006). Limited information goodness-of-fit testing in multidimensional contingency tables. Psychometrika, 71, 713-732. |
| ○ | Mc Leod, D. B. (1994). Research on affect and mathematics learning in the JRME: 1970 to the present. Journal for Research in Mathematics Education, 25(6), 637-647. doi: 10.2307/749576 |
| ○ | Montaño, R. (2009). Una comparación de las estadísticas de bondad de ajuste R1 y M2 para modelos de la Teoría de Respuesta al Ítem (tesis doctoral no publicada). Universidad de Barcelona, Barcelona. |
| ○ | Muraki, E. (1992). A generalized partial credit model: Application of an EM algorithm. Applied Psychological Measurement, 16, 159-176. |
| ○ | Ngussa, B. M. y Mbuti, E. E. (2017). The Influence of Humour on Learners’ Attitude and Mathematics Achievement: A Case of Secondary Schools in Arusha City, Tanzania. Journal of Educational Research, 2(3), 170-181. |
| ○ | Ordóñez, X., Romero, R. y Ruiz, C. (2016). Cuestionario de Actitudes Hacia la Estadística (CAHE): evidencias de validez y fiabilidad de las puntuaciones en una muestra de alumnos de Educación. Bordón, 68(4), 121-136. doi: 10.13042 |
| ○ | Orlando, M. y Thissen, D. (2000). Likelihood-based item fit indices for dichotomous item response theory models. Applied Psychological Measurement, 24, 50-64. |
| ○ | Ostini, R. y Nering, M. L. (2006). Polytomous item response theory models. London: Sage pub. |
| ○ | Ostini, R. y Nering, M. L. (2010). Handbook of Polytomous item response theory models. London: Taylor & Francis Group. |
| ○ | Palacios, A., Arias, V. y Arias, B. (2014). Actitudes hacia las matemáticas: construcción y validación de un instrumento de medición. Revista de Psicodidáctica, 19(1), 67-91. doi: 10.1387 / RevPsicodidact.8961 |
| ○ | Phillips, R. (2007). Mathematics teachers’ beliefs and affects. En F. Lester, Second Handbook of Research on Mathematics Teaching and Learning (pp. 257-315). Charlotte: Information Age Publishing and National Council of Teachers of Mathematics. |
| ○ | Post, W. J, Van Duijn, M. A. J. y Van Baarsen, B. (2001). Tracelines de un solo pico o monótono? En la elección de un modelo IRT para escalar datos. En A. Boomsma, MAJ van Duijn y TAB Snijders (eds.), Ensayos sobre la teoría de la respuesta al ítem (pp. 391-414). Nueva York: Springer. |
| ○ | R Core Team (2017). R: A language and environment for statistical computing. Foundation for statistical Computing. Vienna, Austria. Recuperado de http://www.r-project.org/ |
| ○ | Reckase, M. D. (2009). Multidimensional item response theory. New York: Springer. |
| ○ | Roberts, D. M. y Bilderback, E. W. (1980). Reliability and validity of a statistics attitude survey. Educational and Psychological Measurement, 40, 235-238. doi: 10.1177/001316448004000138 |
| ○ | Rodríguez, O. y Mora, S. (2016). Análisis psicométrico del instrumento Actitudes hacia las Matemáticas mediante el modelo de Respuesta Graduada de Samejima. Actualidades en Psicología, 30(120), 7-30. doi: 10.15517/ap.v30i120.18722 |
| ○ | RStudio Team (2018). RStudio: Integrated Development for R. RStudio, Inc. Boston, Massachusetts. Recuperado de http://www.rstudio.com/ |
| ○ | Samejima, F. (1969). Estimation of latent ability using a response pattern of graded scores. Psychometrika Monograph, 17, 3-21. |
| ○ | Schau, C., Stevens, J., Dauphine, T. y Del Vecchio, A. (1995). The development and validation of the survey of attitudes towards statistics. Educational and Psychological Measurement, 55(5), 868-875. doi: 10.1177/0013164495055005022 |
| ○ | Syyeda, F. (2016). Understanding Attitudes Towards Mathematics (ATM) using a Multi-modal Model: An Exploratory Case Study with Secondary School Children in England. Cambridge Open-Review Educational Research e-Journal, 3, 32-62. Recuperado de http://corerj.soc.srcf.net/?page_id=224 |
| ○ | Tarazona, E., Bazán, J. y Aparico, A. (2013). Actitudes hacia la estadística en universitarios peruanos de mediana edad. Revista Digital de Investigación en Docencia Universitaria, 1, 58-76. |
| ○ | Tshabalala, T. y Ncube, A. C. (2016). Causes of poor performance of ordinary level pupils in mathematics in rural secondary schools in Nkayi district: Learner’s attributions. Nova Journal of Medical and Biological Sciences, 15(1), 122-136. |
| ○ | Vendramini, C. M. M., Silva, M. C. R. D. y Dias, A. S. (2009). Assessment of psychology students' attitudes through credit partial model of IRT. Psico-USF, 14(3), 287-298. doi: 10.1590/S1413-82712009000300005 |
| ○ | Wise, S. (1985). The development and validation of a scale measuring attitudes toward statistics. Educational and Psychological Measurement 2(45), 401-405. doi: 10.1177/001316448504500226 |
| ○ | Yao, L. y Schwarz, R. D. (2006). A multidimensional partial credit model with associated item and test statistics: An application to mixed-format tests. Applied Psychological Measurement, 30(6), 469-492. |
Analysis of the items of the questionnaire of attitudes towards statistics test: use of the multidimensional generalized partial credit model
INTRODUCTION. The Questionnaire of Attitudes towards Statistics (QATS) (Ordóñez, Romero and Ruiz de Miguel, 2016) has been recently proposed, which has evidence of validity and reliability for the measurement of attitudes towards statistics. However, it requires a more exhaustive analysis of the items to extend the evidence of validity. METHOD. Therefore, in the present study the objective is to expand the evidence of the psychometric quality of the QATS, through the application of the Multidimensional Model of Generalized Partial Credit (MMGPC) of the Item response theory (IRT). The QATS was applied to an incidental sample composed of 836 students from the Faculty of Education of the Complutense University of Madrid. The QATS is composed of three dimensions: the scale of negative emotions, the scale of positive emotions and the utility scale, with a total of 16 items on a Likert scale with 5 response options ranging from “completely disagree” to “completely agree”. For the analysis of the items, the program R version 3.4.3 has been used. RESULTS The results show that the questionnaire behaves following a 3-dimensional structure. The results of the parameters of the items allow us to affirm that we have items that discriminate a lot from people with low and high attitudes and that a medium-high level of attitude is required to choose the highest categories of the items. DISCUSSION. Therefore, the results allow us to extend the validity previously reported, being to date one of the few tests with evidence of validity at the level of construct and items.
Keywords: Multidimensional Model of Generalized Partial Credit, Attitudes, Statistic, Item response theory, University students, Likert scale.
Analyse des items de l’épreuve CAHE: utilisation du modèle Multidimensionnel de credit partiel géneralisé
INTRODUCTION. Récemment il a été proposé le Questionnaire d’Attitudes vers la statistique (—CAHE— Ordóñez, Romero et Ruiz de Miguel, 2016) qui a montré une évidence de validité et fiabilité pour mesurer les attitudes vers la statistique. Néanmoins, il faut analyser encore ses items afin d’élargir son évidence de validité. MÈTHODE. À cette fin, l’objectif de cette étude sera élargir l’évidence de la qualité psychométrique du CAHE, au moyen de l’application du modèle multidimensionnel de crédit partiel généralisé (MMCPG) de Théorie des Réponses aux Items (TRI). Il a été appliqué le CAHE sur une échantillon occasionnel composée de 836 étudiants de la Faculté d’Éducation de l’Université Complutense de Madrid (Espagne). Le CAHE est composé de trois dimensions: l’échelle d’émotions négatives, l’échelle d’émotions positives et l’échelle d’utilité, comprenant un total de seize items en échelle type Likert avec cinq options allant de “absolument en désaccord” jusqu’à “absolument d’accord”. Pour l’analyse des items il a été employé le programme R version 3.4.3. RÉSULTATS. Les résultats montrent que le questionnaire s’articule autour trois dimensions. Les résultats qui offrent les paramètres des items permettent d’affirmer qu’il y a d’items qui discriminent des personnes qui ont des attitudes de bas et haut niveau, en plus, il est nécessaire un niveau moyen-haut en attitude afin d’élargir les catégories des items plus élevés. DISCUSSION. Finalement, les résultats permettant élargir la validité des items, sont jusqu’à présent, une des rares épreuves avec une évidence de validité par rapport à la construction du modèle et ses items.
Mots-clés: Modèle multidimensionnel de crédit partiel généralisé, Attitudes, Statistique, Théorie des réponses aux items, Etudiants universitaires, Echelles de Likert.
Covadonga Ruiz de Miguel (autora de contacto)
Doctora en Filosofía y Ciencias de la Educación por la UCM, con Premio Extraordinario de Doctorado. Es profesora titular de universidad en el Departamento de Métodos de Investigación y Diagnóstico en Educación, de la Facultad de Educación (UCM). Imparte docencia en asignaturas de Métodos de Investigación y Estadística Aplicada a las Ciencias Sociales en los Grados de Infantil y Pedagogía y es coordinadora del Grado en Pedagogía de la UCM. Miembro del Grupo de Investigación de Medida y Evaluación de Sistemas Educativos (Grupo MESE, UCM) desde su inicio en 2005.
Correo electrónico de contacto: covaruiz@ucm.es
Dirección para la correspondencia: Facultad de Educación. Dpto. IPE. C/ Rector Royo Villanova, s/n, 28010 Madrid (España).
Xavier G. Ordóñez
Es doctor en Ciencias de la Educación por la UCM, con Premio Extraordinario de Doctorado. Es profesor ayudante doctor en el Departamento de Métodos de Investigación y Diagnóstico en Educación de la Facultad de Educación (UCM). Imparte docencia en asignaturas de Medición Educativa y Estadística Aplicada a las Ciencias Sociales en los Grados de Educación Infantil, Social y Pedagogía.
Correo electrónico de contacto: xavor@edu.ucm.es
Delia Arroyo Resino
Doctora en Educación (UCM), licenciada en Pedagogía (UCM) con Premio Extraordinario y Máster en Estudios Avanzados de Pedagogía (UCM) y Metodología de las Ciencias del Comportamiento y la Salud (UCM, UAM y UNED). Actualmente, profesor universitario de la Universidad Internacional de La Rioja (UNIR), del Departamento de Métodos de Investigación y Diagnóstico en Educación (MIDE). Miembro del Grupo de Investigación de Medida y Evaluación de Sistemas Educativos (Grupo MESE, UCM) desde el año 2014.
Correo electrónico de contacto: delia.arroyo@unir.net